Особливості кіл змінного синусоїдного струму.

Електричні елементи, з яких складається електричне коло, оцінюються за характеристиками: опори – вольт-амперними u = f(i) - залежність напруги від струму (рис. 2.11); індуктивності – вебер-амперними Y = f(i) - залежність потокозчеплення від струму; ємності – кулон-вольтовими q = f(u) - залежність величини заряду від напруги. Якщо елемент має характеристику у вигляді прямої лінії, то такий елемент називають лінійним (опір, індуктивність, ємність). Якщо ж характеристика елементу є не пряма, то такий елемент називають нелінійним. Коло яке містить виключно лінійні електричні елементи називають лінійним електричним колом. Коло в якому є принаймні один нелінійний елемент називають нелінійним електричним колом.

Якщо це коло постійного струму, то при незмінних величинах напруги джерела та опору резистора струм кола також буде незмінним. У сталому режимі постійний струм забезпечує незмінність потужності P = UI резистора, енергії магнітного поля котушки W_м= LI²/2 і енергії електричного поля конденсатора W_С = СU²/2. При цьому, ЕДС самоіндукції e_L = - Ldi/dt в котушці відсутня, а наявність конденсатора в колі взагалі рівнозначне розриву самого кола. Енергетичні параметри такого кола можуть змінюватися тільки у перехідних режимах.

У колах синусоїдного струму фізичні процеси відбуваються дещо складніше.

Так, згідно закону Джоуля-Ленца, у провіднику (резисторі) електрична енергія безповоротно перетворюється у теплову. Разом з тим, за однаковий час, при однаковій силі струму, в одному і тому ж провіднику в колах постійного і змінного струмів виділяється різна кількість теплоти. Пояснюється це тим, що зі збільшенням частоти струму його густина у центральних шарах провідника зменшується, а у поверхневих навпаки – збільшується (явище поверхневого ефекту). Нерівномірність розподілення густини струму призводить до неповного використання перерізу провідника і тому один і той же провідник має більший опір в колах змінного струму, ніж в колах постійного струму.

Опір, в якому електрична енергія безповоротно перетворюється у теплову, у колах постійного струму прийнято називати омічним R, Ом, а в колах змінного струму – активним r, Ом.

Окрім цього, дія змінного струму супроводжується ще двома явищами, які суттєво відрізняють кола змінного струму від кіл постійного струму. Одне з цих явиш полягає у тому, що при проходженні змінного струму в котушці безперервно індукується ЕРС самоіндукції. Друге, пов’язано з тим, що будь-яке коло змінного струму веде себе і як конденсатор, тобто має певну ємність. Для урахування цих фізичних явищ у теорії змінного струму використовують поняття – реактивний індуктивний x_L, Ом, і реактивний ємнісний x_С, Ом, опори.

Отже, фізична суть цих опорів полягає в тому, що в реактивному індуктивному опорі електрична енергія перетворюється в енергію магнітного поля, а в реактивному ємнісному – в енергію електричного поля. Причому, протягом періоду змінного струму енергії цих полів можуть бути перетворені в електричну енергію.

Оскільки реальні електричні кола можуть мати всі три види опорів (r, x_L, x_C) одночасно, то для опису їх результуючого впливу на дію змінного струму використовують поняття – повний опір електричного кола Z, Ом.

2.3.2. Основні закони кіл синусоїдного струму.

Закон Ома – миттєве значення струму кола (ділянки, вітки, елемента) прямо пропорційне миттєвому значенню прикладеної напруги і обернено пропорційне повному опору кола (ділянки, вітки, елемента):

,

або у комплексній формі – комплекс струму кола (ділянки, вітки, елемента) прямо пропорційний комплексу прикладеної напруги і обернено пропорційний комплексу повного опору кола (ділянки, вітки, елемента):

.

Перший закон Кірхгофа – алгебраїчна сума миттєвих значень струмів у будь-якому вузлі електричного кола дорівнює нулю:

.

Іншими словами – сума миттєвих значень струмів, що спрямовані до будь-якого вузла електричного кола, дорівнює сумі миттєвих значень струмів спрямованих від цього вузла.

Для кола синусоїдного струму, де діють струми однієї і тієї ж частоти і їх значення надані комплексними числами, перший закон Кірхгофа можна записати так:

.

Тобто, алгебраїчна сума комплексів діючих значень струмів у будь-якому вузлі кола синусоїдного струму дорівнює нулю. Іншими словами – сума векторів струмів, що спрямовані до будь-якого вузла електричного кола, дорівнює сумі векторів струмів спрямованих від цього вузла.

Другий закон Кірхгофа – у будь-якому замкненому контурі електричного кола алгебраїчна сума миттєвих значень ЕРС, що діють у цьому контурі, дорівнює алгебраїчній сумі миттєвих значень спадів напруги на окремих ділянках контуру –

,

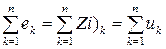де Z – повний опір k-ої ділянки контуру кола.

Для будь-якого замкненого контуру кола синусоїдного струму, де діють джерела ЕРС однієї і тієї ж частоти, другий закон Кірхгофа у комплексній формі можна записують так:

,

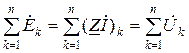де 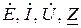– відповідно комплекси діючих значень ЕРС джерела, струму, напруги та комплекс повного опору кола.

Тобто, алгебраїчна сума комплексів діючих значень ЕРС джерел у будь-якому замкненому контурі кола синусоїдного струму, дорівнює сумі комплексів спадів напруг на окремих ділянках цього контуру. Іншими словами – сума векторів спадів напруг на окремих ділянках будь-якого кола синусоїдного струму дорівнює вектору ЕРС, прикладеної до цього кола.