Сцинтилляционная и ПП гаммоспектрометрия.
9.1. В службе радиационной безопасности заводов, СЭС, а также в радиохимии возникает необходимость определить природу повышенной радиации, т.е. идентифицировать. Такая необходимость возникает при обращении с радиоактивными отходами, на участках радиоактивного загрязнения при котором перемещения радиоактивных элементов, приеме-передаче ядерной продукции и в др. ситуациях.
Для решения таких задач во многих случаях бывает достаточно определить состав Е излучения по образцам, пробам данного участка, т.е. получить сведения об энергетическом спектре данного излучения.
Энергетический спектр излучения – распределение частиц или γ-квантов по энергии излучения. Его выражают в виде графиков-спектров, где по горизонт оси откл. Е, а по вертикальной –частоту ( вероятность) излучения частиц данной Е.
Радиоактивное излучение с определенной Е может быть моноэнергетическим (дискретное) и непрерывное (сплошное)
Моноэнергетическое излучение.
В моноэнергетич. излучении частицы вылетают хаотично, и все имеют одну Е0.
Е = f (t) = Е0
Спектром является т. Р(Е0) с координатами ( Е = Е0; Р=1) В таком излучении каждая частица имеет Е0, т.е. вероятность излучения част. = 1 с Е0.
Пр: 137Cs (Е0 = 0,661 МэВ); 241 Am (Е0 = 59,5 кэВ); 54Mn (Е0 = 0,84 МэВ).
Дискретные спектры наз-ся дискретным излучением. В этом излучении вылетают частицы с отдельными значениями энергий. (2-3; 5-7)
Частицы вылетают хаотично и распределяются по трем Е: Е1, Е2, Е3.
в) Непрерывные (сплошные) излучения – сплошное, вылетают частицы с любыми Е в некотором интервале от ЕI до ЕII .
P=f(E)
Моноэнергетические и дискретные спектры характерны для α – и γ – излучения, а сплошные спектры характерны для β-излучения, при этом мах. вероятность характерна для энергии Е=1/3 Еmax.
На графике непрерывного спектра каждому значению Е соотв. Pi. Практически мы не можем измерить точное число частиц Ni ~ Ei , можно лишь измерить число частиц N инт, в некотором интервале Е (i ± ∆ ), близкого к энергии Еi.
Тогда вероятность появления частиц в данном интервале равна:
Ринт i = 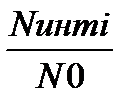 где N0 – общее кол-во частиц в интервале от ЕI до ЕII.
где N0 – общее кол-во частиц в интервале от ЕI до ЕII.
По координатам Р инт i, Е (i ± ∆) можно построить кривую спектра:
Вероятность появления частиц с Е = ЕI ÷ ЕII, равна единице. Ее можно принять равной площади фигуры SI-II, тогда вероятность появления частицы с интервальным значением энергии Е i ± ∆ будет равна
Р =
Где S I ± ∆ - произведение энергии на ширину интервала:
S i ± ∆ = Рi * 2∆
Дата добавления: 2016-12-08; просмотров: 557;
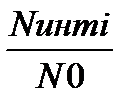 где N0 – общее кол-во частиц в интервале от ЕI до ЕII.
где N0 – общее кол-во частиц в интервале от ЕI до ЕII.