Символьное дифференцирование.

Символьное дифференцирование в MATLAB выполняет команда

diff(func [, var, n])

где func – символьная запись функции или ее имя; var – переменная дифференцирования (если этот параметр отсутствует, то в качестве переменной дифференцирования будет выбрана первая по алфавиту символьная переменная); n – порядок (номер) производной, которую требуется определить (по умолчанию ищется первая производная).

Итак, для вычисления производной функции 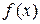необходимо задать выражение, описывающее функцию и обратиться к функции diff.

Вычислим, например, производную от 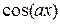по переменной :

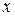>> syms a x

>> f=cos(a*x)

f =

cos(a*x)

>> diff(f)

ans =

-a*sin(a*x)

Вычислим производную от функции 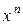по переменной :

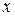>> syms x y n

>> y=x^n

y =

x^n

>> diff(y,x)

ans =

n*x^(n - 1)

Вычислим производную от функции 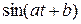по переменной :

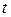>> syms a b t

>> y=sin(a*t+b)

y =

sin(b + a*t)

>> diff(y,t)

ans =

a*cos(b + a*t)

Вычислим теперь производную от функции 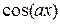по параметру :

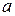>> syms a x

>> f=cos(a*x)

f =

cos(a*x)

>> diff(f,a)

ans =

-x*sin(a*x)

Для вычисления вторых производных по переменной 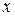и параметру 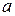можно использовать следующие команды:

>> diff(f,2)

ans =

-a^2*cos(a*x)

>> diff(f,a,2)

ans =

-x^2*cos(a*x)

Вычислим производную четвертого порядка от 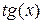по переменной :

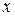>> diff('tan(x)',x,4)

ans =

16*tan(x)*(tan(x)^2 + 1)^2 + 8*tan(x)^3*(tan(x)^2 + 1)

Рассмотрим теперь примеры отыскания производных функций многих переменных различных порядков.

Вычислим частные производные от функции 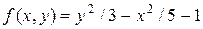по переменным 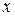и :

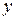>> syms x y

>> diff('y^2/3-x^2/5-1',x)

ans =

-(2*x)/5

>> diff('y^2/3-x^2/5-1',y)

ans =

(2*y)/3

Вычислим частные производные второго порядка от функции 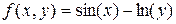по переменным 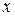и :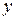

>> diff('sin(x)-ln(y)',x,2)

ans =

-sin(x)

>> diff('sin(x)-ln(y)',y,2)

ans =

1/y^2

Очевидно, что несложным образом можно вычислить и производную от параметрической функции. Так, например, для функции, определяемой уравнениям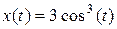и и 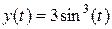, будем иметь:

>> syms t

>> x=sym('3*cos(t)^3')

x =

3*cos(t)^3

>> y=sym('3*sin(t)^3')

y =

3*sin(t)^3

>> diff(y)/diff(x)

ans =

-sin(t)/cos(t)

Вычислим производную от матрицы

.

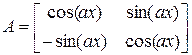Имеем:

>> A=[cos(a*x) sin(a*x); -sin(a*x) cos(a*x)]

A =

[ cos(a*x), sin(a*x)]

[ -sin(a*x), cos(a*x)]

>> diff(A)

ans =

[ -a*sin(a*x), a*cos(a*x)]

[ -a*cos(a*x), -a*sin(a*x)]