Ось автомобильной дороги представляет собой пространственную линию, состоящую из прямолинейных и криволинейных участков.
Проекцию оси автомобильной дороги на горизонтальную плоскость, с изображением элементов рельефа и ландшафта называют планом трассы (положение оси автомобильной дороги на местности).
Проекция оси автомобильной дороги (по поверхности покрытия проезжей части) на вертикальную плоскость, проходящую через саму ось, называют продольным профилем.
Поперечный уклон – термин, относящийся к поперечному профилю (сечение вертикальной плоскостью, перпендикулярной к оси трассы).
Уклон – отношение превышения к заложению. Безразмерная величина, равная тангенсу угла между наклонным участком и его горизонтальной проекцией. Выражается в промилле ‰ (тысячные).
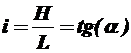
при малых значениях α
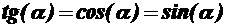
С целью формулирования требований к геометрическим элементам оси автомобильной дороги, рассмотрим силы, действующие на автомобиль, при его ускоренном движении на подъём:
-сопротивление движению на подъём 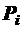 ;
;
-сопротивление качению (трение качения) 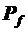 ;
;
-инерция автомобиля  ;
;
-сопротивление воздуха 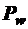
Движение автомобиля представляется возможным, если выполняется условие тягового баланса:
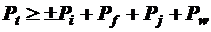 , где
, где
 [H] – тяговое усилие, развиваемое расчётным автомобилем
[H] – тяговое усилие, развиваемое расчётным автомобилем
Приложение 03_02
"Требования к геометрии автомобильной дороги"
Сопротивление движению на подъём с уклоном i, определяется работой, совершаемой двигателем для перемещения автомобиля на единицу высоты. Если принять длину участка 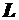 , а превышение его конечной точки над начальной
, а превышение его конечной точки над начальной 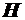 , то, пренебрегая всеми остальными силами, действующими на автомобиль, работа двигателя будет равна:
, то, пренебрегая всеми остальными силами, действующими на автомобиль, работа двигателя будет равна:
 ;
;
 [кг] – масса автомобиля;
[кг] – масса автомобиля;
 [м/с2] – ускорение свободного падения
[м/с2] – ускорение свободного падения
Отнесём работу двигателя, по перемещению автомобиля на высоту 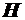 , к длине участка
, к длине участка 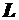 , получим значение силы, необходимое для преодоления уклона i в каждой его точке:
, получим значение силы, необходимое для преодоления уклона i в каждой его точке:
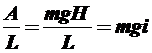
Очевидно, если условие 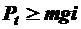 не выполняется, то движение автомобиля становится невозможным. Иначе, пренебрегая всеми другими силами, действующими на автомобиль, можно определить допустимое значение продольного уклона из условия возможности движения расчётного автомобиля:
не выполняется, то движение автомобиля становится невозможным. Иначе, пренебрегая всеми другими силами, действующими на автомобиль, можно определить допустимое значение продольного уклона из условия возможности движения расчётного автомобиля:
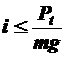
Разумеется, в случае реальных расчётов необходимо рассматривать совокупность действия всех сил сопротивления. Кроме того, предельные значения, полученные в результате подобного расчёта, не являются удовлетворяющими с точки зрения скоростного режима и комфортности движения. Поэтому необходимо вводить некоторые коэффициенты запаса.
Сопротивление качению вызывается на идеально ровном покрытии затратами энергии на преодоление деформации пневматических шин, а также упругие и пластические деформации дорожной одежды. Логично, что сопротивление качению складывается из соответствующих значений для каждого колеса автомобиля:
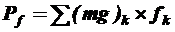 , где
, где
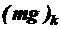 [H] – доли силы тяжести, приходящиеся на отдельные колёса;
[H] – доли силы тяжести, приходящиеся на отдельные колёса;
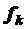 [1] – соответствующие коэффициенты сопротивления качению
[1] – соответствующие коэффициенты сопротивления качению
Обычно коэффициент сопротивления качению относят к общему весу автомобиля, то есть, считают, что:
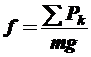
Значения коэффициентов сопротивления качению варьируются в зависимости от материала и состояния поверхности покрытия. Для асфальтобетонных и цементобетонных покрытий f = 0,01 – 0,02; для грунтовой дороги с неровностями f = 0,15. Логично, что коэффициент сопротивления качению, и собственно, само сопротивление качению в реальных условиях является функцией ровности.
Сопротивление инерционных сил будем рассматривать в контексте тягового баланса исключительно как инерцию поступательного движения. Однако не стоит забывать о том, что на криволинейных участках в плане, инерционные силы будут определять уровень безопасности движения, но этот вопрос рассмотрим отдельно. Кроме того, часть мощности двигателя расходуется на преодоление инерции вращающихся частей, что должно быть учтено при оценке реальных динамических характеристик автомобиля. С учётом перечисленных ограничений, сопротивление инерционных сил будет выражаться соотношением:
 , где
, где
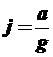 [1] – относительное ускорение автомобиля;
[1] – относительное ускорение автомобиля;
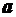 [м/с2] – поступательное ускорение автомобиля
[м/с2] – поступательное ускорение автомобиля
 [кг] – масса автомобиля;
[кг] – масса автомобиля;
 [м/с2] – ускорение свободного падения
[м/с2] – ускорение свободного падения
Сопротивление воздушной среды вызывается тремя причинами:
-давлением встречного воздуха на переднюю часть автомобиля;
-трением воздуха о боковую поверхность автомобиля;
-затратой мощности на преодоление сопротивления завихрений воздушных струй за автомобилем, вблизи колёс и под кузовом.
Согласно законам аэродинамики, сопротивление воздушной среды будет равным:
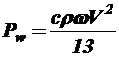 , где
, где
 [1] – коэффициент сопротивления среды (безразмерная величина, зависящая от очертания и формы тела, а также от гладкости его поверхности);
[1] – коэффициент сопротивления среды (безразмерная величина, зависящая от очертания и формы тела, а также от гладкости его поверхности);
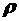 [кг/м3] – плотность воздуха;
[кг/м3] – плотность воздуха;
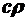 [кг/м3] – коэффициент сопротивления воздуха, определяемый экспериментально;
[кг/м3] – коэффициент сопротивления воздуха, определяемый экспериментально;
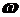 [м2] – площадь проекции автомобиля на плоскость, перпендикулярную направлению его движения;
[м2] – площадь проекции автомобиля на плоскость, перпендикулярную направлению его движения;
 [м/с] – относительная скорость движения автомобиля и воздушной среды.
[м/с] – относительная скорость движения автомобиля и воздушной среды.
Задавшись характеристиками расчётного автомобиля и значением расчётной скорости можно определить значения допустимых продольных уклонов для определённых условий движения. Необходимо отметить, что значения продольных уклонов автомобильной дороги в числе прочего определяют затраты горючего при движении автомобилей, а следовательно, и транспортную составляющую себестоимости перевозок. Потому назначение продольных уклонов логично рассматривать ещё и в контексте эффективности транспортной работы.
На трудных участках дорог в горной местности длины затяжных участков с уклонами более 60 ‰ ограничивают в зависимости от высоты участка над уровнем моря.
Значения предельно допустимых продольных уклонов определяются значением расчётной скорости, следовательно, при их определении учитывались динамические характеристики расчётного автомобиля (мощность неодинакова при различных передачах и скоростях движения).
Приложение 03_03
"Требования к геометрии автомобильной дороги"
Далее рассмотрим криволинейные участки в продольном профиле и условия движения по ним. В случае движения по выпуклой вертикальной кривой на автомобиль действует сила инерции, направленная от центра кривизны.
При этом вес автомобиля (сила, с которой он воздействует на поверхность покрытия) уменьшается. Пренебрегая, значением угла между векторами центробежной силы и силы тяжести, можно записать, что вес автомобиля изменится (уменьшится) на величину, равную значению центробежной силы:
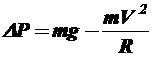 , где
, где
 [м/с] – скорость движения автомобиля;
[м/с] – скорость движения автомобиля;
 [м] – радиус вертикальной кривой
[м] – радиус вертикальной кривой
В силу уменьшения веса автомобиля, снижается и значение коэффициента сцепления. Коэффициент сцепления: безразмерная величина, равная отношению тягового усилия на ободе ведущего колеса к доле силы тяжести автомобиля, приходящейся на это колесо в момент проскальзывания:

Фактически, коэффициент сцепления характеризует предельное значение тягового усилия, по отношению к силе тяжести, приходящейся на данное колесо. При большем значении тягового усилия связь между поверхностью покрытия и колесом теряется, начинается пробуксовывание. (для а/б покрытий 0,5)
Полагая коэффициент сцепления постоянной величиной, характеризующей только качественное состояние поверхности покрытия проезжей части, очевидно, что максимальное тяговое усилие (по сути характеризующее устойчивость автомобиля) снижается вместе со значением веса автомобиля. Это изменение пропорционально квадрату скорости движения и обратно пропорционально радиусу вертикальной кривой. Поэтому для больших значений расчётной скорости из условия устойчивости автомобиля необходимо вводить большие радиусы вертикальных кривых.
В случае движения автомобиля по вогнутой вертикальной кривой, центробежная сила, напротив, приводит к увеличению его веса. Логично предположить, что в этом случае устойчивость автомобиля повышается (максимально возможное значение тягового усилия возрастает). Но вместе с тем, возрастает и нагрузка на ходовую часть автомобиля. Так, для расчётной скорости 80 км/ч, при движении по вогнутой вертикальной кривой радиусом 1000 м, значение центробежной силы составит:
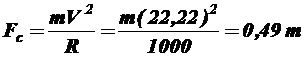
Приложение 03_04
"Требования к геометрии автомобильной дороги"
Инерционные силы действуют на автомобиль и при его движении на кривой в плане (в горизонтальной плоскости). При определённом сочетании скорости движения и радиуса кривизны возможен занос автомобиля или его опрокидывание. Поэтому для определения минимально допустимого радиуса кривой в плане следует исходить из значения расчётной скорости.
Рассмотрим случай движения автомобиля по участку проезжей части с поперечным уклоном i. Запишем сумму проекций всех сил, действующих на автомобиль, на ось, проходящую через его центр масс и параллельную поверхности покрытия проезжей части:
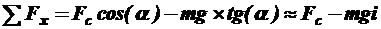
Раскрывая значение центробежной силы и, учитывая возможность различного направления поперечного уклона, получим:

Для того чтобы получить относительный показатель, характеризующий условия движения на кривой в плане, независящий от массы автомобиля, разделим полученную сумму на значение силы тяжести:
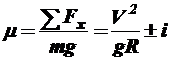
Полученный коэффициент называют коэффициентом поперечной силы. Он показывает, какую долю составляет сумма всех сил, которые стремятся сместить автомобиль с кривой при данных сочетаниях радиуса, скорости движения и поперечного уклона проезжей части по отношению к силе тяжести, действующей на автомобиль. Выразим значение радиуса:
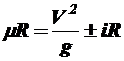 ;
; 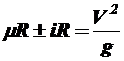 ;
; 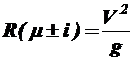 ;
; 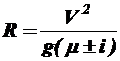
Таким образом, получили выражение для определения допустимого значения радиуса кривой в плане при определённой величине расчётной скорости. Условия движения при этом будут характеризоваться коэффициентом поперечной силы:
-при m < 0,10 – кривая пассажирами не ощущается;
-при m = 0,20 – ощущается и пассажир испытывает неудобства;
-при m = 0,30 – въезд с прямого участка на кривую ощущается как толчок, наклоняющий пассажиров в бок;
-при m > 0,6 – автомобиль может опрокинуться.
Так, для расчетной скорости 150 км/ч, и коэффициенте поперечной силы, равном 0,15 получим минимально допустимое значение радиусов кривых в плане (поперечный уклон равен 0):

Как видно, поперечный уклон проезжей части может как способствовать, так и препятствовать устойчивости автомобилей на кривой. Так, на участках, где по каким-либо причинам затруднительно обеспечить требуемое минимальное допустимое значение радиуса кривой, проезжей части придают определённый поперечный уклон с увеличением высотных отметок от центра кривой. Плавное изменение поперечного уклона на подходах к криволинейному участку называется вираж. Поперечные уклоны проезжей части на виражах варьируются в зависимости от радиусов кривых. Переход от двускатного поперечного профиля к односкатному следует осуществлять на переходных кривых.
В пределах переходных кривых происходит плавное изменение радиуса от ∞ в начале до радиуса основной (круговой кривой) в конце. Переходные кривые с круговой вставкой называют составной кривой. Составные кривые необходимо проектировать при радиусе кривизны менее 3000 м на автомобильных дорогах I технической категории и менее 2000 м для II-V технических категорий. Виды переходных кривых: радиоидальная спираль, лемниската, кубическая парабола, коробовые кривые.
Величина радиуса кривой определяет также расстояние видимости в плане. Таким образом, минимально допустимые радиусы кривых в плане определяются из условия устойчивости автомобиля на кривой и обеспеченности расстояния видимости.
Радиусы смежных кривых в плане не должны отличаться более чем в 1,3 раза (коэффициент безопасности). Не рекомендуется короткая прямая вставка между двумя кривыми в плане, направленными в одну сторону. При длине менее 100 м рекомендуется заменять обе кривые одной, большего радиуса, при длине 100 – 300 м рекомендуется заменять прямую вставку переходной кривой большего параметра.
Помимо криволинейных участков в плане, отдельные требования предъявляются и к прямолинейным участкам. Длину прямых вставок ограничивают в зависимости от технической категории и типа рельефа. Так для автомобильной дороги I технической категории предельная длина прямой в плане составляет в равнинной местности 3500 – 5000 м.
Иными словами нагрузка, как на ходовую часть автомобиля, так и на водителя возрастает почти наполовину. При таких условиях движения изнашивание ходовой части автомобиля заметно возрастёт, комфортность движения ухудшится. Водитель воспринимает подобные дорожные условия как опасные и снижает скорость движения, что приводит к снижению пропускной способности таких участков.
Значения радиусов вертикальных кривых определяют расстояние видимости в продольном профиле. Нормируются отдельно значения расстояний видимости для встречного автомобиля и для остановки. Для соответствующих расчётных скоростей эти расстояния должны обеспечить своевременное восприятие водителем внезапно возникающих препятствий в пределах проезжей части и совершение манёвра с целью избежания ДТП (экстренное торможение или объезд препятствия). Наименьшее расстояние видимости для остановки должно обеспечивать видимость любых предметов, имеющих высоту 0,2 м и более, находящихся на середине полосы движения, с высоты глаз водителя автомобиля 1,2 м от поверхности проезжей части.

Достаточно легко оценить зависимость радиусов вертикальных кривых и расстояний видимости графически. Для этого необходимо через каждую точку продольного профиля, выше линии высотных отметок оси проезжей части (красной линии) провести касательную к линии, отражающей высотные отметки в обоих направлениях от точки обзора. Длина отрезков касательных до точек касания будет отражать соответствующие значения расстояний видимости.
Таким образом, требования к допустимым значениям радиусов вертикальных кривых определяются следующими соображениями:
-автомобили при движении с расчётной скоростью не должны терять управляемость и устойчивость на проезжей части;
-уровень нагрузок, вызванных инерционными силами не должен приводить к ухудшению эмоционального восприятия водителем условий движения и изнашиванию ходовой части автомобиля;
-должно быть обеспечено необходимое расстояние видимости.
Приложение 03_05
"Требования к геометрии автомобильной дороги"
Расчёт ширины одной полосы движения
Проезжая часть автомобильной дороги должная иметь ширину, обеспечивающую возможность безопасного движения автомобилей с расчётной скоростью в один или несколько рядов. Если ширина проезжей части будет недостаточной, это вызовет необходимость снижения скорости при встрече автомобилей. Если же назначена избыточная ширина, то будут затрачены неоправданные средства на строительство дорогостоящего покрытия.
Полоса, занимаемая по ширине проезжей части движущимся автомобилем, называется полосой движения. Чем выше скорость движения, тем большая ширина полосы необходима для безопасного движения автомобилей.
Ширина полосы движения может быть определена по формуле:
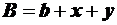 ,
,
где: 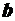 [м] – ширина кузова автомобиля;
[м] – ширина кузова автомобиля;
 [м] – расстояние от крайней точки кузова до смежной полосы;
[м] – расстояние от крайней точки кузова до смежной полосы;
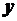 [м] – расстояние от крайней точки кузова до края проезжей части (кромка проезжей части или краевая полоса).
[м] – расстояние от крайней точки кузова до края проезжей части (кромка проезжей части или краевая полоса).
Величины  и
и 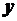 можно принять равными:
можно принять равными:
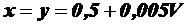 ,
,
При движении в одном направлении:

где:  [м/с] – расчётная скорость движения;
[м/с] – расчётная скорость движения;
Так, для расчётной скорости 120 км/ч (II ТК) получим:
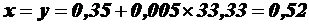 [м]
[м]
Тогда, принимая ширину автомобиля (МАЗ-511), равной 2.70 м, получим ширину полосы движения:
 [м]
[м]
Дата добавления: 2016-05-11; просмотров: 1269;
