Высказывания, зависящие от параметра. Кванторы
Определение 1.8. (1)
Вместо слов "существует", "найдется", "имеется" в логических формулах употребляется символ 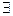 (перевернутая первая буква английского слова exist — существовать), называемый символом (квантором) существования, а вместо слов "любой", "каждый", "произвольный", "какой бы ни" — символ
(перевернутая первая буква английского слова exist — существовать), называемый символом (квантором) существования, а вместо слов "любой", "каждый", "произвольный", "какой бы ни" — символ 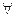 (перевернутая первая буква английского слова all — "все"), называемый символом (квантором) всеобщности.
(перевернутая первая буква английского слова all — "все"), называемый символом (квантором) всеобщности.
Так, запись 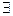 х читается "существует x", а запись
х читается "существует x", а запись 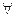 x — "любое x" или "для любого x" или "для всех x". Соответственно запись
x — "любое x" или "для любого x" или "для всех x". Соответственно запись 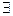 x,
x, 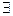 у, или, короче,
у, или, короче, 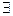 х,у означает "существуют x и y", а запись
х,у означает "существуют x и y", а запись 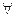 x,
x, 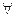 y, или, короче,
y, или, короче, 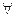 x,y — "любые x и у" или "для любых х и у".
x,y — "любые x и у" или "для любых х и у".
Определение 1.8.(2)
Пусть A(x) – высказывание, причем при разных значениях x оно может иметь разную истинность. x носит название параметра, а A(x) – высказывания, зависящего от параметра.
Например, A = {x2 > 5} для x=1 A(1) ложно, а для x = 11 A(11) – истинно.
Пример 1.8.
Если A(х) — утверждение "х — студент", а утверждение B(x) — "x учится
усердно", то утверждение 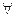 x (A(x)
x (A(x) 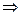 B(x)) может быть интерпретировано как
B(x)) может быть интерпретировано как
"Все студенты учатся усердно". Точно так же, если A(х) — утверждение "х — кот", a B(x) — утверждение "х любит читать", то выражение 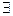 x (A (x)˄ B(x)) может быть сформулировано как "Некоторые коты любят читать". Утверждение "Все люди смертны" логически может быть выражено как
x (A (x)˄ B(x)) может быть сформулировано как "Некоторые коты любят читать". Утверждение "Все люди смертны" логически может быть выражено как 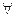 x (A(x)
x (A(x) 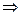 B(x)), где A(х) — утверждение "х — человек", a B(x) — утверждение "х смертен". Аналогично, утверждение "Некоторые целые числа делятся на 5" может быть записано
B(x)), где A(х) — утверждение "х — человек", a B(x) — утверждение "х смертен". Аналогично, утверждение "Некоторые целые числа делятся на 5" может быть записано 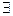 x (A (x)˄ B(x)), где A(х) — утверждение "х
x (A (x)˄ B(x)), где A(х) — утверждение "х
— целое число", a B(x) — утверждение "х делится на 5". Обычно логические выражения, содержащие 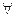 x, можно превратить в утверждения, содержащие "для всех", а логические выражения, содержащие
x, можно превратить в утверждения, содержащие "для всех", а логические выражения, содержащие 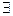 x, можно обратить в утверждения, содержащие "для некоторого".
x, можно обратить в утверждения, содержащие "для некоторого".
В силу такого характера перевода с языка логики на естественные языки и обратно, отрицание утверждения типа "для всех" есть утверждение типа "для некоторого", а отрицание утверждения типа "для некоторого" есть утверждение типа "для всех". Например, отрицание утверждения «Все целые числа являются простыми» есть утверждение Некоторые целые числа не являются простыми, а отрицание утверждения «Некоторые студенты любят ходить на вечеринки» есть утверждение «Все студенты не любят ходить на вечеринки».
Иначе говоря:
Пусть Â = A(x), истинное для всех x, не зависит от параметра
Ă = A(x), истинное хотя бы для одного значения параметра x
 = ( 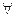 x : A(x) истинно)
x : A(x) истинно)
Ă = ( 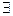 x : A(x) истинно)
x : A(x) истинно)
Построим теперь для них отрицания.
˥ Â = (A ложно хотя бы для одного значения x)
Т.е. ( 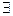 x : A(x) ложно) = (
x : A(x) ложно) = ( 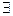 x : ˥A(x) истинно)
x : ˥A(x) истинно)
˥( 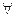 x : A(x) истинно) = (
x : A(x) истинно) = ( 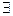 x : ˥A(x) истинно)
x : ˥A(x) истинно)
˥ Ă = (A ложно для всех значений x)= ( 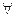 x : A(x) истинно)
x : A(x) истинно)
˥( 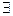 x : A(x) истинно) = (
x : A(x) истинно) = ( 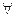 x : ˥A(x) истинно)
x : ˥A(x) истинно)
Замечание 1.8.
Обратите внимание, что при отрицании A(x) меняется на ˥A(x) , квантор 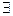 на
на 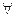 и наоборот, квантор
и наоборот, квантор 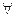 на
на 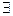 .
.
Дата добавления: 2016-10-17; просмотров: 984;
