Алгоритмы сортировки сравнениями
Рассмотрим один из простейших алгоритмов сортировки сравнениями: так называемую пузырьковую сортировку.
Алгоритм «Пузырьковая сортировка»
1. Повторять:
А. Для всех элементов списка, кроме последнего, повторять:
1. Если текущий элемент больше следующего, то поменять их местами.
2. Конец цикла при условии, что ни одной замены не произошло.
Проиллюстрируем работу алгоритма на примере последовательности из 5-ти чисел: 5, 3, 1, 4, 2. Работа алгоритма пузырьковой сортировки проиллюстрирована на следующем рисунке.
| ► | 5┐ | ► | 3┐ | ► | |||||||||||||||||||||||||||
| 3┘ | ► | 5┐ | 1┘ | ► | ► | 3┐ | |||||||||||||||||||||||||
| 1┘ | ► | 5┐ | ► | 4┐ | 2┘ | ► | |||||||||||||||||||||||||
| 4┘ | ► | 5┐ | 2┘ | ► | ► | ||||||||||||||||||||||||||
| 2┘ |
Видно, что на каждом шаге внешнего цикла самый большой элемент перемещается в конец списка. При этом не обязательно просматривать весь список каждый раз, так как на каждом шаге последний элемент оказывается на своем месте. В связи с этим на каждом шаге можно просматривать на один элемент меньше, и алгоритм можно модифицировать.
Алгоритм «Пузырьковая сортировка»
1. Присвоить переменной k количество элементов списка.
2. Повторять:
А. Уменьшить k на 1.
Б. Для первых k элементов списка повторять:
1. Если текущий элемент больше следующего, то поменять их местами.
3. Конец цикла, при условии, что ни одной замены не произошло.
Сколько времени будет выполняться такая сортировка? За элементарную операцию примем операцию сравнения двух элементов и подсчитаем, сколько таких операций необходимо произвести, если дан список из n элементов. На каждом шаге будет просматриваться на один элемент меньше. В худшем случае (когда исходный массив отсортирован по убыванию) каждый раз будет производиться хотя бы один обмен элементов, пока не останется только один элемент, и сортировку не закончится. На первом шаге будет сделано n-1 сравнение, на втором n-2 сравнения, и т.д. до одного сравнения. Итого, имеем арифметическую прогрессию от 1 до n-1 с n-1 элементом. Сумма этой прогрессии:
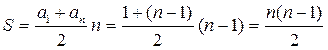 .
.
При больших значениях n эта функция ведет себя как n2. В таком случае говорят, что вычислительная сложность алгоритма равна O(n2). Эта оценка вычислительной сложности алгоритма называется асимптотической. Такая оценка обычно является достаточно плохой. Возникают вопросы: можно ли написать алгоритм, который будет работать быстрее и какой самый быстрый алгоритм вообще можно написать? Ответ – можно, и это 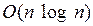 . Невозможно написать более быстрый алгоритм сортировки сравнениями. Для лексикографической сортировки наиболее быстрый алгоритм имеет вычислительную сложность
. Невозможно написать более быстрый алгоритм сортировки сравнениями. Для лексикографической сортировки наиболее быстрый алгоритм имеет вычислительную сложность 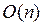 .
.
При сортировке для обмена элементов списка можно использовать дополнительную переменную.
Пример (см. пример из параграфа 6.4)
VAR
Temp:Student;
k,i:Integer;
Stop:Boolean;
. . .
{ Сортировка массива S со списком студентов по
фамилии. Пусть длина списка задана переменной n }
k:=n;
REPEAT
Dec(k);
Stop:=True;
FOR i:=1 TO k DO
IF S[i].Name>W[i+1].Name THEN
BEGIN
Temp:=S[i];
S[i]:=S[i+1];
S[i+1]:=Temp;
Stop:=False;
END;
UNTIL Stop;
Лекция 8
Дата добавления: 2016-09-20; просмотров: 857;
