Рассмотрим еще одну закономерность разомкнутого теодолитного хода.

Предположим на известны приращения координат между смежными точками хода. Тогда, обозначив сумму приращений координат между всеми точками хода через

(SDC)_ТЕОР= DC_Н-1+DC_1-2+...+DC_(n-1)-n , и имея ввиду, что

X_К = X _Н +(SDC)_ТЕОР ,

получим

(SDC)_ТЕОР= X_К - X _{Н .}

Рассуждая аналогично , будем иметь

(SDY)_ТЕОР= Y_К - Y _{Н .}

Теоретическая сумма приращений координат разомкнутого теодолитного хода равна разности координат конечной и начальной точек хода.

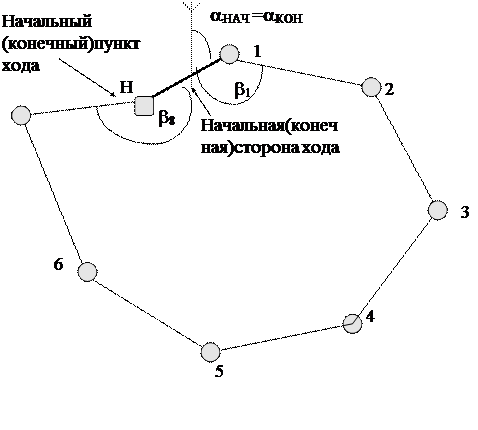
На рисунке показана схема замкнутого теодолитного хода (теодолитного полигона) , опирающегося в начале и конце на один и тот же пункт с известными координатами ( т. Н(X_Н,Y_H) ) и сторону т.Н -т.1 с известным направлением (дирекционным углом a_Н) .

Общее количество точек хода (углов поворота замкнутого многоугольника) равно n , из них n-1 -определяемых.

В ходе n внутренних углов поворота и n сторон.

В основе вычисления координат точек хода теодолитного полигона также как и разомкнутого теодолитного хода лежит последовательное определение координат последующей точки хода от координат его предыдущей точки.

Правые по ходу углы поворота хода являются внутренними углами теодолитного полигона ( замкнутого n - угольника). Тогда

(åb)_ТЕОР = (n -2) 180°.

Теоретическая сумма внутренних углов теодолитного полигона равна 180° умноженные на количество углов полигона без двух.

Рассмотрим еще одну закономерность теодолитного полигона.

Предположим нам известны приращения координат между смежными точками хода. Тогда, обозначив сумму приращений координат между всеми точками хода через

(SDC)_ТЕОР= DC_Н-1+DC_1-2+...+DC_(n-1)-n , и имея ввиду, что

X_К = X _Н +(SDC)_ТЕОР ,

получим

(SDC)_ТЕОР= X_К - X _{Н .}

Но , в теодолитном полигоне X_К = X _Н , следовательно,

(SDC)_ТЕОР=0.

Рассуждая аналогично , будем иметь

(SDY)_ТЕОР= 0 _.

Теоретическая сумма приращений координат теодолитного полигона равна нулю.

Уравнивание теодолитных ходов заключается в сравнении теоретических и измеренных значений сумм углов поворота и приращений координат.

Цель уравнивания вычисление координат точек теодолитного хода.

Уравнивание углов

1. Вычисление суммы измеренных углов

(åb)_пр.=b₁+b₂+...+ b_n-1+b_n .

2. Вычисление теоретической суммы углов

(åb)_ТЕОР =a_Н - a_К + 180°n (для правые)

(åb)_ТЕОР =a_к- a_н + 180°n (для левых)

(åb)_ТЕОР = (n -2) 180°(для замкнутого хода)

3. Вычисление угловой невязки

f _.= (åb)_{пр. -} (åb)_теор.

4. Вычисление допустимой угловой невязки

f_b^доп = 1¢ · Ö n .

5. При условии допустимой невязки вычисление поправок в измеренные углы. Контроль

6.Вычисление исправленных значений углов поворота. Контроль

7.Вычисление дирекционных углов сторон хода. Контроль

Уравнивание приращений координат:

1.Вычисление приращений координат

2.Вычисление суммы вычисленных приращений кооддинат

3.Вычисление теоретической суммы приращений координат

4. Вычисление линейных невязок

5. Вычисление абсолютной линейной невязки

6. вычисление относительной невязки

7. Сравнение невязок в случае допустимости вычисление поправок в приращения координат. Контроль.

8. Вычисление исправленных значений приращений. Контроль

9. Вычисление координат точек теодолитного хода. Контроль