Токи вторичных и первичных обмоток

питающего трансформатора.

Ток, протекающий по вторичным обмоткам трансформатора под действием ЭДС этих обмоток, обусловливает величину тока в нагрузке- I_d. Ток в нагрузке складывается из прямоугольных импульсов фазных токов и, при принятых допущениях является идеально гладким. Вызывает интерес выяснить, какой ток, по форме и по величине, потребляется из питающей сети, и протекает по первичным обмоткам питающего трансформатора. Это нужно знать для того, чтобы можно было ответить на вопрос, как влияет работа вентильного преобразователя на питающую сеть.

Рассмотрим эквивалентную схему неуправляемого вентильного преобразователя (выпрямителя) совмещенную с его питающим трансформатором.

Трансформатор включен по схеме звезда - звезда. Точками обозначены начала обмоток, а стрелками- положительное направление токов. Пренебрегая токами намагничивания трансформатора, ввиду их малости по сравнению с рабочими токами, и, приняв для простоты k_тр =1 (w₁ = w₂), напишем уравнения для магнитных контуров на основании 2-го закона Кирхгофа для магнитных цепей. Для этого обозначим два магнитных контура 1 и 2. Обходить контура будем по направлению, указанному стрелкой. Условимся, что если ток совпадает по направлению с направлением обхода, он берется в уравнении со знаком “+”, если не совпадает- со знаком “-”. В соответствии со 2-ым законом Кирхгофа, сумма токов в каждом замкнутом магнитном контуре должна быть равна нулю.

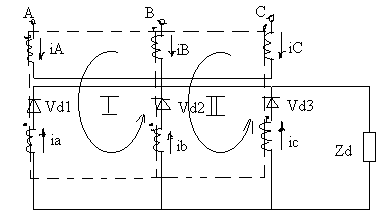
Рис 12

Кроме того, в соответствии с 1-ым законом Кирхгофа, сумма всех трех токов первичных обмоток трансформатора равняется нулю. На основании этих законов запишем систему уравнений:

i_A - i_a + i_b - i_B = 0

i_B - i_b + i_c - i_C = 0 (3-5)

i_A + i_B + i_C = 0

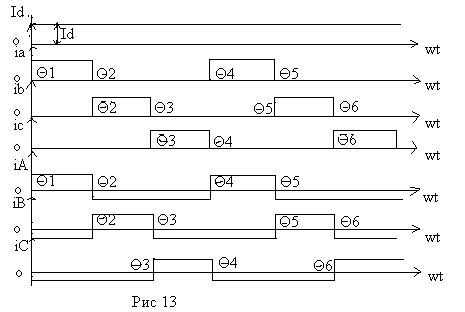
В этой системе шесть неизвестных: три значения первичных токов и три- вторичных. Однако вторичные токи могут быть определены из условий работы схемы. Так для интервала Q₁£ Q£ Q₂ можно записать:

i_a = I_d ; i_b = i_c = 0

Тогда, решая систему, находим значения первичных токов:

i_A= (2/3) I_d ; i_B =i_C = -(1/3) I_d

Аналогично, для интервала Q₂£ Q£ Q₃ можно найти:

i_B = (2/3) I_d ; i_A =i_C = -(1/3) I_d

Для интервала Q₃£ Q£ Q₄ :

i_C= (2/3) I_d ; i_A =i_B = -(1/3) I_d .

При принятых условиях и допущениях (k_тр =1, трансформатор и вентили идеальные) диаграммы токов во всех обмотках трансформатора выглядят следующим образом:

При к_тр > 1 ((w₁/w₂)>1) первичные токи будут в k_тр раз меньше, чем те, которые определены по полученным формулам.

Так для интервала Q₁£ Q£ Q₂

i_A= (1/ k_тр)*(2/3) I_d и т.д.

Суммарная намагничивающая сила по каждому из стержней в данной схеме оказывается отличной от нуля. Так, например, в стержне фазы А действует н.с. на интервале Q₁£ Q£ Q₂ :

F_A = (i_a - i_A)*w = (I_d - (2/3) I_d )*w = (1/3)w *I_d

на интервале Q₂£ Q£ Q₄ :

F_A = (i_a - i_A)*w = (0 - (1/3) I_d )*w = (1/3)w *I_d

Аналогичное наблюдается в других стержнях трансформатора. Таким образом, характерной особенностью трехфазной нулевой схемы является наличие нескомпенсированных намагничивающих сил и, вызванных ими потоков вынужденного намагничивания. Эти потоки замыкаются частично по сердечнику, по стальной арматуре трансформатора, частично по воздуху и при больших токах нагрузки могут привести к насыщению магнитопровода.

Для избежания этого приходится завышать сечение магнитопровода и, тем самым, утяжелять трансформатор. Это является причиной того, что трехфазная нулевая схема в практике применяется нечасто и только для небольшой мощности электропривода. Поток вынужденного намагничивания возникает и при соединении первичных обмоток трансформатора по схеме “треугольника”.

В других схемах преобразователей форма первичных токов отличается от рассмотренного выше.

Так, в трехфазной мостовой схеме форма первичного тока симметрична относительно нулевого значения и имеет следующий вид:

Рис 13 а)

Существует закономерность: чем ближе форма первичного тока питающего трансформатора к синусоиде, тем выше энергетические показатели схемы.

Существуют и используются схемы преобразователей с более высокими частотами пульсаций: двенадцатипульсные, двадцатичетырехпульсные и, даже, сорокавосьмипульсные. В них первичный ток по форме еще ближе приближается к синусоиде.