МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ.
Изучить самостоятельно в доступных учебниках.
5.6.
|
Рассмотрим колебания, описываемые уравнением (5.8) – свободные колебания. Воспользовавшись математическим формализмом решения однородных дифференциальных уравнений второго порядка (аналогично тому, как мы сделали при решении уравнения гармонических колебаний (5.5)), можно получить решение уравнения (5.8) , которое имеет вид:
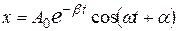(5.28)
где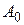 
и 
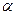- константы, которые определяются начальными условиями движения в каждом конкретном случае, а частота 
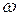, с которой происходят колебания –частота свободных колебаний
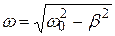(5.29)
Обратите внимание на то, что частота свободных колебаний меньше частоты собственных, и различие между ними возрастает с ростом затухания!
Очевидно, что в этом случае система совершает колебания, близкие к гармоническим, с амплитудой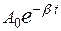 
, зависящей от времени. Примерный вид свободных колебаний показан на рисунке 5.3. Важно понимать, что колебания в этом случае являются ангармоничесчкими, т.е. негармоническими, поскольку не описываются гармоническим законом.
Скорость затухания (быстрота уменьшения амплитуды) колебаний определяется величиной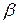 
, называемой коэффициентом затухания. Его физический смысл заключается в том, что это величина, обратная времени 
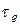, в течение которого амплитуда колебания уменьшается в 
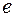раз. Действительно, уменьшение амплитуды в 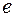раз означает, что 
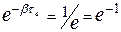(множитель уменьшился в 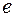раз). Поэтому 
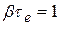т.е.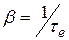 
.
Наибольший практический интерес представляет ситуация, когда затухание не слишком велико: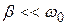 
. В этом случае частота и период свободных колебаний мало отличаются от частоты и периода собственных колебаний. При этом с ростом затухания период свободных колебаний возрастает:
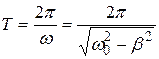(5.30)
Для характеристики степени затухания колебаний, кроме коэффициента затухания, используется также логарифмический декремент затухания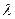 
:
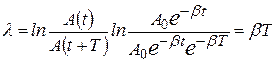. (5.31)
Его физический смысл заключается в том, что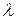 
обратен числу колебаний 
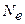, совершаемых за время, пока амплитуда колебаний уменьшается в 
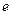раз: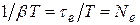 
.
Для характеристики колебательной системы часто используется величина
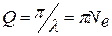, (5.32)
называемая добротностью колебательной системы. Эта величина пропорциональна числу колебаний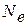 
, совершаемых за время, пока амплитуда колебаний уменьшается в 
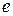раз.
Колебательные системы с очень большим затуханием также встречаются на практике. При увеличении затухания частота колебаний (5.29) проходит через нуль и становится мнимой. Соответственно период колебаний с ростом затухания возрастает до бесконечности и также становится мнимым. Нулевая частота означает отсутствие колебаний, точнее бесконечность периода колебаний.
Математически это соответствует тому, что решение уравнения (5.8) оказывается сумой двух вещественных экспонент, убывающих со временем. Физически это означает, что движение системы носит апериодический характер, т.е. система возвращается в положение равновесия, не совершая колебаний. При этом возможны два способа (рисунок 5.4) такого движения, отличающиеся начальными условиями: при отклонении от положения и предоставлении системы самой себе она плавно стремится к положению равновесия. Если системе сообщить дополнительную энергию, толкнув ее после отклонения к положению равновесия, то она может пересечь положение равновесия, но так и не завершит полного колебания.
Дата добавления: 2016-06-02; просмотров: 563;