Виды обеспечения САПР

Структурирование САПР по различным аспектам обусловливает появление видов обеспечения САПР. Принято выделять семь видов обеспечения:

· техническое обеспечение (ТО), включающее различные аппаратные средства (ЭВМ, периферийные устройства, сетевое коммутационное оборудование, линии связи, измерительные средства);

· математическое обеспечение (МО), объединяющее математические методы, модели и алгоритмы для выполнения проектирования;

· программное обеспечение (ПО), представляемое компьютерными программами САПР;

· информационное обеспечение (ИО), состоящее из баз данных (БД), систем управления базами данных (СУБД), а также включающее другие данные, используемые при проектировании;

· лингвистическое обеспечение (ЛО), выражаемое языками общения между проектировщиками и ЭВМ, языками программирования и языками обмена данными между техническими средствами САПР;

· методическое обеспечение (МетО), включающее различные методики проектирования, иногда к МетО относят также математическое обеспечение;

· организационное обеспечение (ОО), представляемое штатными расписаниями, должностными инструкциями и другими документами, регламентирующими работу проектного предприятия.

В данном курсе рассматривается математическое обеспечение САПР.

При решении задач конструкторского проектирования можно условно выделить этапы:

· ввод и контроль информации;

· построение формальной модели схемы, т.е. разбиение электрической схемы на конструктивно законченные части;

· компоновка;

· размещение;

· трассировка;

· выдача конструкторской документации.

Из всего комплекса задач технического проектирования самой важной является задача разбиения электрических схем на конструктивно законченные части. От результата решения данной задачи зависит качество решения последующих задач технического проектирования.

В качестве математической модели электрической схемы проектируемых устройств используется теория графов. С помощью этой теории удобно строить алгоритмы оптимизации, пригодные для реализации на компьютере.Под построением формальной модели схемы имеется в виду переход от схемы к графу.

Лекция 1

Основные понятия теории графов

Граф Gсостоит из множества вершин Х (точек) и множества ребер U (линий) соединяющих между собой все или часть вершин. Обозначение графа G=(X;U). Запись u_ijÎU означает, что ребро графа u_ij=(x_i,x_j) образовано парой вершин x_i и x_j, x_iÎX, x_jÎX. Таким образом, ребра- это упорядоченные пары вершин.

С помощью графов можно отразить наиболее общие свойства объектов (топологические свойства), отвлекаясь от их геометрических форм и размеров.

Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Для такого графа u_kj=(x_k,x_j)¹(x_j,x_k)=u_jk - это различные ребра

Если ребра не имеют ориентации, граф называется неориентированным.

Для него u_kj=(x_k,x_j)=(x_j,x_k)=u_jk.

Пример:

Вершины: здания; ребра: прямые улицы

В нашем курсе изучаются неориентированные графы. Две вершины x_i и x_j называются смежными, если существует ребро u_ijÎU, соединяющее эти вершины. Другими словами, смежными называются вершины, прилегающие к одному и тому же ребру.

Ребро u_ij инцидентно вершинам x_i, x_j, если оно связывает эти вершины. Ребра u_kl, u_lm называются смежными, если они имеют общую вершину (в примере вершина l).

Мультиграф –граф, любые две вершины которого связаны более чем одним ребром. В таком графе ребра, связывающие одну и ту же пару вершин, называются кратными. Мультичисло - наибольшее число кратных ребер в графе.

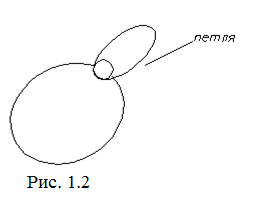
Петли – ребра графа, у которых обе концевые вершины совпадают, то есть u_ij=(x_i,x_j), i=j (рис. 1.2).

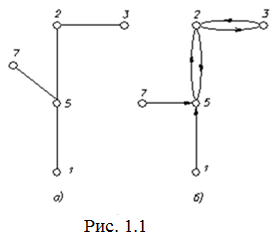
Число ребер, инцидентных некоторой вершине, называют степенью вершины, обозначается p(x). Для графа на рис 1(а) p(x₅)=3, p(x₁)=1. Легко увидеть, что если сложить степени всех вершин графа, то получится четное число равное удвоенному числу ребер, так как каждое ребро участвует в сумме 2 раза. Этот результат называют леммой Эйлера о рукопожатиях (если несколько человек обменялись рукопожатием, то число пожатых рук – четно). Из этой леммы следует, что