Физические модели; материальная точка, система материальных точек, абсолютно твердое тело, сплошная среда.

Физика, изучая реальные объекты, абстрагируется от тех или иных свойств объекта и учитывает только те наиболее важные черты, которые существенные для данной задачи. Т.о. возникают физические модели, т.е. идеализированные объекты, которые изучаются с точки зрения решения конкретных физических задач.

Существуют следующие физические модели:

1. Материальная точка.

2. Система материальных точек.

3. Абсолютно твердое тело.

4. Сплошная среда.

Простейшая модель – это материальная точка – которой называется любое тело, размерами которого можно пренебречь.

Очень многие физические величины являются аддитивными (суммирование), поэтому можно рассматривать тела, которые не являются материальными точками, как системы материальных точек. Тогда, записав для каждой точки выражения для аддитивной величины можно эти выражения сложить и получить.

Системы материальных точек могут образовывать 2 вида моделей: абсолютно твердое тело, сплошная среда.

Абсолютно твердое тело – такая система материальных точек, в которой расстояние между материальными точками не изменяется, т.е. тело не деформируется ни при каких условиях.

Сплошная среда – это такая система материальных точек, в которой расстояние между двумя точками пренебрежительно мало.

1.1. Пространство и время. Кинематическое описание движения, элементы векторной алгебры

Определение фундаментальных понятий, одна из наиболее сложных задач любой науки. Это в полной мере касается понятия пространства.

Древние Греки под пространством понимали вместилище всех вещей.

В современные физике понятие пространства является более общим в том смысле, что свойства пространства могут меняться в зависимости от тех или иных физических процессов, более того некоторые физические явления рассматривают как проявление тех или иных свойств в пространстве (гравитация). С точки зрения механики, пространство представляет собой то вместилище, в котором описываются положения объектов.

Положение тела или точки в пространстве можно задать с помощью координат. Для этого вводятся системы координат.

Система координат – когда выбрано тело отсчета и через какую-нибудь его точку проводят оси координат и положение любой точки в пространстве описывают ее координатами.

Положение тела или точки можно задать относительно какого-нибудь другого тела, которое называется телом отсчета.

Системы координат бывают различными: прямоугольные и косоугольные, полярные, сферические и другие.

Наиболее часто используется декартова система координат. Это прямоугольная система координат, состоящая из трех взаимно перпендикулярных осей, распределенных в пространстве определенным образом.

Развитие тех или иных процессов в физике происходит с течением времени, т.е. время играет роль параметра (переменной), от которой могут зависеть те или иные физические величины. С точки зрения современной физики и само время может зависеть от тех или иных физических процессов (релятивистская физика). Т.о. мы подошли к тому, чтобы сформулировать основную задачу механики, т.е. ту задачу, которая решается всеми тремя разделами механики.

Эта задача состоит в том, чтобы знать положение тела или точки в любой момент времени, или знать зависимость от времени координат тела или точки. Такая зависимость называется кинематическим законом движения, она может быть записана в виде:

ìx=f₁(t)

íy=f₂(t) Координатный способ записи. (1.1)

îz=f₃(t)

или в виде:

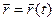Векторная форма записи. (1.2)

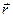- радиус-вектор данной точки.

Можно показать, что эти две формы записи представления кинематического закона движения взаимосвязаны. Для этого необходимо знать, что такое радиус-вектор и как он выражается через координаты.

Радиус-вектор точки – это вектор, проведенный из начала координат в данную точку.

.

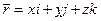Через каждую точку пространства можно провести радиус-вектор. 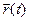- эта формула описывает движение конца вектора в пространстве.

.

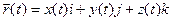Физический смысл - координаты изменяются со временем.

Механическое движение описывается при помощи ряда основных кинематических понятий и величин: траектория, путь, перемещение, скорость, ускорение.

Траектория – линия, которую описывает конец радиус-вектора .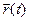

Перемещение тела (материальной точки) - направленный отрезок прямой, соединяющий начальное положение с его последующим движением.

Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка.

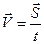, или

Скорость – величина, измеряемая длиной пути, проходимого в единицу времени.

Ускорение – величина, численно равная изменению скорости в единицу времени.

Путь – длина линии, пройденной за время _Dt.

1.2. Скорость и ускорение при криволинейном движении. Нормальное и касательное ускорение

Скорость, как векторная величина, может меняться двояко, по направлению и по величине или модулю. В общем случае меняется и по величине и по направлению, как показано на рисунке. При этом вектор изменения скорости можно разбить на два вектора (см. рисунок). Один из них характеризует изменение 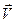только по направлению 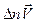, а второй характеризует изменение 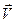только по величине .

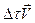Можно написать соотношение между общим изменением 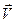и тангенциальным изменением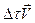

.

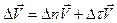Если разделить левую и правую часть на время _Dt, за которое произошло изменение и выполнить предельный переход при _Dt®0, то мы получим соотношение, которое свяжет между собой полное ускорение 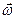, нормальное 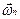, тангенциальное или касательное .

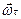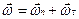. (1.4)

Можно показать, что в случае, когда _Dt®0 направление нормального ускорения будет перпендикулярно к вектору скорости, а касательное ускорение направлено вдоль вектора скорости, поэтому эти два ускорения – нормальное и касательное – взаимно перпендикулярны. Следовательно формулу (1.4) модно переписать в скалярном виде:

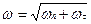. (1.5)

Нормальное ускорение в курсе элементарной физики изучалось при равномерном движении материальной точки по окружности (центростремительное ускорение).

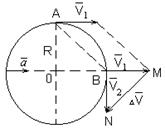
Рассмотрим равномерное движение материальной точки по окружности и выведем формулу для центростремительного движения.

При криволинейном движении .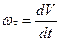

При вращательном .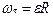

Центростремительное ускорение возникает в результате изменения скорости по направлению.

, , ,

,

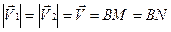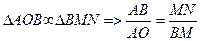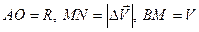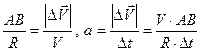при _Dt®0 (мгновенное ускорение) AB®l_{AB ,}

_.

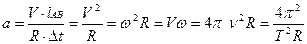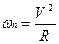. (1.6)

Нужно представить через угловые коэффициенты:

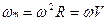. (1.7)

При помощи нормального и касательного ускорений можно проклассифицировать движение.

Зададим.

1. 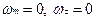- равномерное прямолинейной.

2. 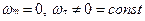- прямолинейное равноускоренное.

3. 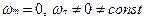- прямолинейное ускоренное движение.

4. 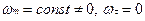- равномерное движение по окружности.

5. 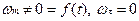- равномерное по дуге переменного радиуса.

6. 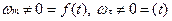- Ускоренное движение по криволинейной траектории. Здесь нужно рассмотреть движение тела, брошенного под углом к горизонту и доказать, что это движение подходит к пункту 6.

1.3. Прямолинейное движение точки. Движение точки по окружности. Угловая скорость и угловое ускорение. Вектор угловой скорости.

График зависимости скорости от времени:

.

.

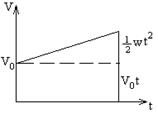
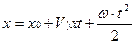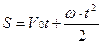Равноускоренное прямолинейной движение – движение, при котором скорость тела, движущегося по прямой за любые равные промежутки времени изменяется одинаково.

.

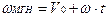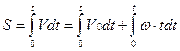
Графиком зависимости пути от времени является парабола.

Ускорение – прямая, параллельная оси времени.

Для примера рассмотрим частный случай, когда ускорение зависит от времени линейно:

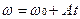, (1.8)

где А – коэффициент пропорциональности, описывающий данную зависимость

Общая формула для вычисления скорости:

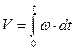. (1.9)

Подставив (1.8) в (1.9), получим:

.

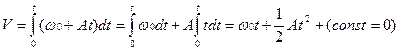Формула скорости имеет вид квадратичной зависимости.

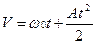, t=0, V₀=0 (1.10)

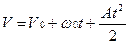, t=0, V₀¹0.

По аналогичной схеме можно получить формулу для пути или координаты для данного пути.

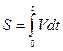(1.11)

Если в формулу (1.11) подставить формулу (1.10) и проинтегрировать, то получится зависимость пути от времени:

.

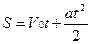В данном случае могут быть и более сложные зависимости от времени основных физических величин (путь, скорость, ускорение). Определяющими являются зависимости от времени для ускорения.

Эти зависимости обычно вытекают из рассмотрения динамической части задачи.

Движение по окружности.

Особенность этого движения состоит в том, что траекторией является окружность. Это значит, что радиус кривизны траектории должен быть постоянным.

Поэтому нормальное и тангенциальное (касательное) ускорения могут принимать разные значения, но при условии что радиус кривизны траектории будет при этом постоянным.

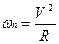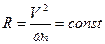. (1.12)

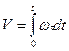(1.13)

Подставив (1.13) в (1.12) получим:

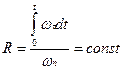(1.14)

Эта формула накладывает ограничения на значения нормального и тангенциального ускорения, когда тело или точка движется по окружности.

Наряду с линейными величинами движение по окружности может описываться угловыми кинематическими величинами: угловой скоростью, перемещением, ускорением.

Угловая скорость – вектор w, который численно равен первой производной от угла поворота j по времени t и направленный вдоль неподвижной оси вращения так, чтобы из его конца вращение тела было видно происходящим против часовой стрелки.

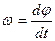или

угловая скорость равномерного движения (w) есть величина, измеряемая углом поворота в единицу времени.

Угловое ускорение – это величина, которая характеризует быстроту изменения угловой скорости.

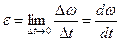(1.15)

где 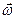- угловая скорость.

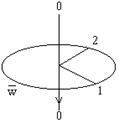
Угловые величины являются псевдовекторами. Это значит, что они имеют направления, но эти направления выбираются при помощи некоторых правил. А именно угловое перемещение и угловая скорость направлены по правилу правого винта.

Прямая ОО является осью вращения, точка переходит из положения (2) в (1), т.е. движется по часовой стрелке. Вектор угловой скорости направлен в ту сторону, вдоль оси вращения, куда перемещался бы правый винт, если его вращать по направлению движения точки.

Вектор углового ускорения может иметь 2 возможных направления. Он может быть направлен по направлению вектора угловой скорости, в том случае, когда угловая скорость со временем растет, или противоположно вектору угловой скорости в том случае, когда вектор угловой скорости с течением времени уменьшается.

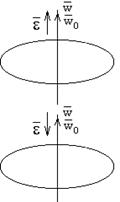Если конечная угловая скорость меньше начальной, то угловое ускорение направлено в обратную сторону.

Для угловой скорости и ускорения общие формулы имеют такой же вид как и для аналогичных линейных величин.

Поэтому можно используя схему, примененную для линейных величин, получить формулы для основных угловых кинематических величин для двух случаев - равномерного движения по окружности и равноускоренного движения по окружности.

Движение равномерное, если числовое значение его угловой скорости не изменяется с течением времени w=const. В этом случае угол поворота тела зависит линейно от времени j=wt.

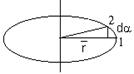Установим связь между угловыми и линейными кинематическими величинами. Рассмотрим движение материальной точки по окружности, положение точки в каждый момент времени можно охарактеризовать при помощи вектора 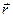, а изменение положения точки при помощи угла поворота вектора 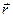da. Этот угол и является модулем углового перемещения. Длина дуги окружности между положениями точки (1) и (2) dl в том случае, когда da достаточно мал, может быть заменена на длину хорды, соединяющей эти точки. Из геометрии известно, что между указанными величинами имеется связь:

(1.16)

Это же соотношение может быть записано и векторно, если учесть правило, по которому находится направление вектора углового перемещения и то, что хорда dl является линейным перемещением.

Все три величины являются взаимно перпендикулярными векторами, они составляют правую тройку векторов. Это означает, что векторная формула связи между этими величинами имеет вид:

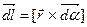(1.17)

Формулы (1.16) и (1.17) являются исходными. Если продифференцировать эти отношения по времени, то получим соотношение между угловой и линейной скоростью.

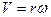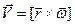, (1.18)

Если продифференцировать по времени (1.18), то получим формулы, связывающие угловое и линейное ускорение:

.

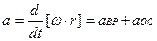1.4. О смысле производной и интеграла в приложениях к физическим задачам.

С точки зрения математики производная и интеграл представляют собой следующее:

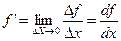(1.19)

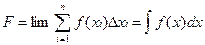(1.20)

Из этих формул видно, что и в том и в другом случае выполняется предельный переход при _Dx®0, т.е. изменение аргумента функции выбирается бесконечно малым.

Физика не оперирует бесконечно малыми величинами, поэтому в физике под величиной dx понимается конечная, но в то же время достаточно маленькая величина.

Малость этой величины в каждом конкретном случае определяется условиями задачи, а именно _Dx (dx) должно быть настолько малым, чтобы изменение функции, которая зависит от аргумента x оказалось пренебрежимо маленьким.

Это значит, что мы какую-то следующую задачу с переменными величинами сведем к задаче более простой с величинами постоянными.

Пример. Если вычисляется скорость, то в случае равномерного движения

.

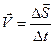В случае движения с переменной скоростью, выбирая разные значения _Dt мы получили разные значения скоростей

, .

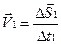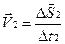Эти скорости являются средними скоростями за соответствующие промежутки времени, однако, если выбирать _Dt меньше и меньше, то начиная с некоторых значений отношение _DS к _Dt перестанет заметно меняться и в конце концов мы добьемся, что это отношение будет практически постоянным (его изменение пренебрежительно мало).

Таким образом мы сводим задачу о движении с переменной скоростью к задаче о движении с постоянной скоростью:

.

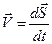Пример. Пусть необходимо вычислить плотность некоторого вещества, вещество неоднородно.

Плотность величина переменная, тогда выбирая разные значения объема _DV мы получим разные значения плотностей:

.

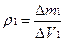
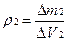Это средние значения по соответствующим объемам.

Если выбирать _DV все меньше и меньше, то будет достигнута такая ситуация, когда плотность перестанет заметно меняться и получим:

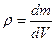(1.21)

Таким образом при помощи производной решается задача о вычислении величин локальных или мгновенных, т.е. соответствующих либо данному моменту времени, либо некоторой точке пространства.

При помощи интегрирования решается обратная задача, т.е. по значениям мгновенных величин или локальных вычисляются значения величин, соответствующих либо некоторому временному интервалу, либо некоторой области пространства.

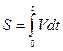
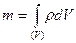(1.22)

1.5. Кинематическое описание движения жидкости.

Жидкость в механике рассматривается как сплошная среда. Ее кинематическое описание возможно двумя различными способами.

1 способ: прослеживается движение каждой частицы жидкости. Для каждой частицы жидкости в каждый момент времени должны быть записаны значения ее координат и скорости.

2 способ заключается в том, что наблюдатель находится в определенной точке пространства, через которую движутся разные частицы жидкости, и фиксирует в каждый момент времени скорость этих разных частиц жидкости. Как правило используется 2 способ, он является наиболее простым.

При этом в каждой точке пространства можно сопоставить вектор скорости, которой обладают частицы жидкости проходя через эту точку.

Совокупность таких векторов скоростей называется полем скоростей.

Если построить геометрическое место точек, в каждой из которых вектор скорости направлен по касательной, то получится некоторая линия, которая называется линией тока. Ее можно провести через любую точку пространства.

Если вектора скоростей, составляющих поле скоростей с течением времени не меняются ни по модулю, ни по направлению, то такое движение жидкости называется стационарным.

Выделим в жидкости при помощи замкнутого контура некоторую совокупность линий тока. Эти линии тока составляют трубку тока.

Основные свойства трубки тока заключаются в том, что частицы жидкости не выходят за ее пределы. Т.е. трубка тока ведет себя, как вела бы себя труба с жесткими стенками, по которой течет жидкость.

Рассмотрим трубку тока, имеющую разные площади сечения S₁ и S₂, и выясним, как зависит скорость течения жидкости от площади сечения.

Вычислим массу жидкости, проходящую через каждое из сечений за один и тот же промежуток времени _Dt. Частицы жидкости проходят за это время расстояние равное V_Dt. Будем считать, что _Dt достаточно мало, чтобы пренебречь изменением площади сечения на этой длине, тогда

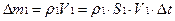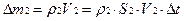, (1.23)

Из закона сохранения массы и условия неразрывности жидкости следует, что

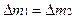(1.24)

Подставим (1.23) в (1.24), сократим на _Dt, получим:

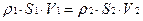(1.25)

Жидкость, плотность которой всюду одинакова и изменяться не может, называется несжимаемой.

Если считать жидкость несжимаемой, то

r₁=r₂ (1.26)

Тогда (1.25) приобретет вид:

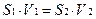, или

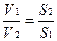(1.27)

Т.о. скорость течения жидкости обратно пропорциональна площади сечения, через которую эта жидкость проходит.

ГЛАВА 2. ДИНАМИКА ЧАСТИЦ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.

2.1. Основная задача динамики. Понятие состояния классической механики. Границы применимости классического способа описания движения частиц.

Опр.: Динамикой называется часть механики, изучающая динамическое движение, в связи с теми причинами, которые определяют характер движения.

Такими причинами являются взаимодействия между телами.

Основная задача динамики состоит в постановке и поиске решения двух следующих задач:

1. По заданным силам (взаимодействиям) следует установить законы движения тел или точек – прямая задача.

2. По заданным законам движения вычислить силы, действующие на точки или тела – обратная задача.

В классической механике понятия состояния движения частицы в любой момент времени характеризуется положением частицы и величиной скорости. Т.о. необходимо в каждый момент времени точно знать значения координат частицы и ее скорости. При этом образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. Такой способ описания движения частиц имеет принципиальное ограничение.

Согласно квантовой механике, которая обобщает классическую для микромира, невозможно в каждый момент времени знать с одинаковой точностью значения координат частицы и ее скорости. Это вытекает из соотношений неопределенности Гейзенберга, имеющий следующий вид:

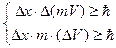(1.28)

_Dx – неопределенность координаты,

_DV – неопределенность скорости.

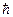- постоянная Планка.

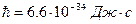
Значение постоянной Планка очень мало, порядок величины составляет 10^-34 Дж×с. Поэтому ограничение по классическому описанию частиц актуальны главным образом для микрочастиц, т.е. частиц с очень маленькой массой. В каждом конкретном случае вопрос о том, какое описание приемлемо, классическое или квантовое, решается при помощи исследования данной задачи. Как правило, ограничения на неопределенность какой-либо одной величины бывают известны, тогда из соотношения (1.28) можно вычислить неопределенность второй величины и сравнить полученное значение со значением самой этой величины. Если они одного порядка, то классическим описанием пользоваться нельзя. Если неопределенность гораздо меньше, чем сама величина, то классическим описанием пользоваться можно.

2.2. Первый закон Ньютона. Понятие инерциальной системы отсчета.

Если на материальную точку или тело не действуют никакие другие тела или их действие компенсируется, то тело называется свободным.

Движение свободного тела называется движением по инерции.

1 закон Ньютона описывает такое движение. Отметим, что 1 закон Ньютона содержится еще в работах Галилея. Но Ньютону принадлежит только формулировка.

Закон. Всякое тело сохраняет состояние покоя ил равномерного прямолинейного движения, если на него не действуют никакие другие тела или их действие компенсируется.

Следствие. Движение по инерции представляет собой равномерное прямолинейное движение.

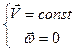(2.1)

Говоря о равномерном движении или состоянии покоя, необходимо учитывать систему отсчета, относительно которой рассматривается движение.

Т.е. 1 закон Ньютона нельзя формулировать относительно к какой-либо системе отсчета. Возникает вопрос - во всех ли системах отсчета он справедлив. Оказывается не во всех. Есть такие системы отсчета, в которых 1 закон Ньютона справедлив, называющиеся инерциальными системами отсчета (ИСО). Т.о. 1 закон Ньютона из всех возможных систем отсчета выделяет класс инерциальных. Отсюда вытекает другая формулировка 1 закона Ньютона.

Система отсчета – совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов.

1 закон Ньютона называется законом инерции, а инерцией называется свойство тел сохранять величину и направление скорости, когда на него не действуют силы (или действуют уравновешенные силы).

ИСО является система отсчета, начало которой связано с центром Солнца, а оси направлены на неподвижные звезды (называется гелиоцентрической).

2.3. Масса и сила. Эталон массы . Уравнения движения. 2 закон Ньютона как уравнение движения. Сила, как производная импульса.

Если попытаться изменить состояние движения какого-либо тела, то тело будет при этом оказывать определенное сопротивление. Это свойство тел называется инертностью.

Количественной характеристикой инертности тела является массы.

Масса – мера инертности тела. Это скалярная физическая величина, которая измеряется в СИ в кг. Обозначается:

[m] =кг.

Для того, чтобы измерить массу какого-либо тела, необходимо эту массу сравнить с массой эталона. Например, рассмотрим взаимодействие двух тел, массами m₁ и m₂, в результате взаимодействия скорость первого тела изменилась на _DV₁, а второго на _DV₁. Эксперименты показывают, что всегда выполняются условия.

,

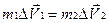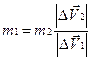(2.2)

Если вместо m₂ взять массу эталона, то по формуле (2.2) можно вычислить массу любого тела. Кроме понятия массы для дальнейшего описания потребуется описание силы.

Силой называется физическая векторная величина, характеризующая взаимодействие тел.

В настоящее время физике известно 4 вида взаимодействия, а именно:

– гравитационное

– электромагнитное

– слабое

– сильное

Последние 2 взаимодействия описывают процессы в микромире. Сильное взаимодействие описывает взаимодействие между частицами внутри ядра атома. Слабое описывает процессы взаимного превращения элементарных частиц. Эти взаимодействия являются короткодействующими, проявляются на очень маленьких расстояниях. Оба они не характеризуются понятием силы. Понятие силы характерно для гравитационного и электромагнитного взаимодействий, причем в механике используются не все проявления взаимодействия, а только некоторые:

– Силы гравитационного притяжения.

– Сила тяжести.

– Проявление электромагнитного взаимодействия.

– Сила упругости нити.

– Сила трения.

– Сила упругости деформированного тела.

– Сила реакции опоры.

1. Сила трения. Трение подразделяют на внешнее и внутреннее. .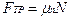

2. Сила упругости.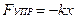

3. Сила гравитационного взаимодействия. .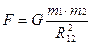

Для того, чтобы решить основную задачу механики, обычно приходится решать (интегрировать) уравнения движения, имеющие следующий вид:

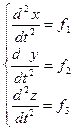(2.3)

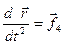или (2.4)

Функции f₁, f₂, f₃, f₄ определяются характером взаимодействия тел и могут зависеть от координат и времени. Для того, чтобы понять откуда эти функции берутся, сформулируем 2 закон Ньютона. Существует несколько формулировок. Простейшая формулировка:

Закон. Когда на тело действует одна сила и масса тела не меняется, то ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе.

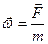(2.5)

Если учесть, что ускорение вторая производная от пути, то

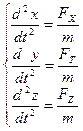(2.6)

Т.о. 2 закон Ньютона представляет собой уравнение движения тела.

Более сложный случай возникает, если на тело действует несколько сил. Тогда 2 закон Ньютона имеет следующую формулировку:

Закон. Ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.

Под равнодействующей мы понимаем сумму всех сил.

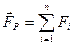(2.7)

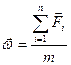(2.8)

Из формулы 2 закона Ньютона получается размерность силы:

,

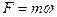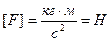
Еще более общий случай 2 закона Ньютона возникает, когда необходимо учесть возможность изменения массы тела.

Для того, чтобы сформулировать 2 закон Ньютона введем понятие импульса тела (количества движения) – это физическая векторная величина, численно равная произведению массы тела на скорость и направленная в сторону движения тела. Обозначается:

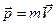(2.9)

Формулировка 2 закона Ньютона имеет вид:

Закон. Скорость изменения импульса тела равна равнодействующей всех сил, действующих на это тело.

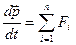(2.10)

Если (2.9) подставить в (2.10), то формула приобретет следующий вид:

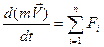(2.11)

Если m постоянна,, то ее можно вынести за знак производной.

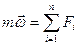(2.12)

Это означает, что последняя формулировка 2 закона Ньютона является самой общей.