Асимметрия. Эксцесс.

Приведем краткий обзор характеристик, которые наряду с уже рассмотренными применяются для анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.

Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия – момента статистического ряда.

Определение. Начальным выборочным моментом порядка 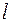называется среднее арифметическое 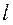- х степеней всех значений выборки:

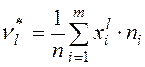или .

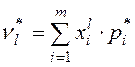Из определения следует, что начальный выборочный момент первого порядка: .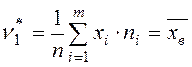

Определение. Центральным выборочным моментом порядка 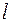называется среднее арифметическое 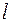-хстепеней отклонений наблюдаемых значений выборки от выборочного среднего :

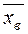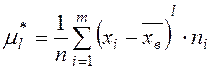или .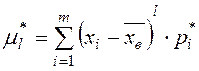

Из определения следует, что центральный выборочный момент второго порядка :

.

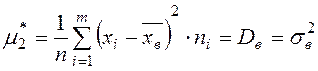Определение. Выборочным коэффициентом асимметрииназывается число 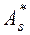, определяемое формулой: .

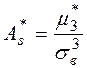Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.

Если , то более пологий «спуск» полигона наблюдается слева; если 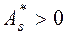- справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.

Определение. Выборочным коэффициентом эксцесса или коэффициентом крутости называется число , определяемое формулой :

.

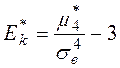Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением.

Коэффициент эксцесса для случайной величины, распределенной по нормальному закону, равен нулю.

Поэтому за стандартное значение выборочного коэффициента эксцесса принимают .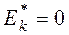

Если , то полигон имеет более пологую вершину по сравнению с нормальной кривой; если 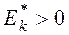, то полигон более крутой по сравнению с нормальной кривой.