Единицы физических величин. Система единиц СИ
Единица измерения физической величины – физическая величина фиксированного размера, которой условно присвоено числовое значение, равное 1, и применяемая для количественного выражения однородных с ней физических величин.
Совокупность основных и производных единиц физических величин, образованная в соответствии с принципами для заданной системы физических величин называется системой единиц физических величин.
Единица физической величины, входящая в принятую систему единиц, называется системной.
В РФ используется международная система единиц СИ, устанавливаемая ГОСТ 8.417 – 2002 «ГСИ. Единицы величин».
Единицы, входящие в систему, делятся на основные (единица основной физической величины в данной системе) и производные (единица производной физической величины системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или с основными и уже определенными производными).
Производные единицы бывают когерентными– производная единица физической величины, связанная с другими единицами системы единиц уравнением, в котором числовой коэффициент равен 1. Пример: единица «ньютон» является когерентной единицам «метр, килограмм, секунда»: 1 Н = м·кг·с-2.
Таблица 2.1 – Основные единицы системы СИ
| Величина | Единица | ||
| наименование | рекомендуе-мое обозна-чение | наименование | обозначение |
| Длина | l | метр | м |
| Масса | m | килограмм | кг |
| Время | t | секунда | с |
| Сила электрического тока | I | ампер | А |
| Термодинамическая температура | T | кельвин | К |
| Количество вещества | n, ν | моль | моль |
| Сила света | J | кандела | кд |
Таблица 2.2 – Пример производных единиц системы СИ
| Величина | Единица | ||
| наименование | обозна-чение | выражение через основные единицы | |
| Плоский угол | радиан | рад | м·м-1 = 1 |
| Телесный угол | стерадиан | ср | м2·м-2 = 1 |
| Частота | герц | Гц | с-1 |
| Сила | ньютон | Н | м·кг·с-2 |
| Давление | паскаль | Па | м-1·кг·с-2 |
| Энергия, работа, количество теплоты | джоуль | Дж | м2·кг·с-2 |
| Мощность | ватт | Вт | м2·кг·с-3 |
| Электрическое напряжение, электрический потенциал, разность электрических потенциалов, ЭДС | вольт | В | м2·кг·с-3·А-1 |
| Электрическая емкость | фарад | Ф | м-2·кг-1·с4·А2 |
| Электрическое сопротивление | ом | Ом | м2·кг·с-3·А-2 |
ГОСТ 8.417 устанавливает разрешенные к применению наравне с единицами СИ единицы других систем и внесистемные единицы – единица физической величины, не входящая в принятую систему единиц (таблица 2.3).
Таблица 2.3 – Пример внесистемных единиц, допускаемых к применению наравне с единицами системы СИ
| Величина | Единица | ||
| наименование | обозна-чение | выражение через единицы СИ | |
| Масса | тонна | т | 1·10-3 кг |
| Объем, вместимость | литр | л | 1·10-3 м3 |
| Энергия | киловатт-час | кВт·ч | 3,6·106 Дж |
| Сила | дина | дин | 1·10-5 Н |
| килограмм-сила | кгс | 9,80665 Н | |
| Мощность | лошадиная сила | л.с. | 735,499 Вт |
| Давление | бар | бар | 1·105 Па |
Также стандарт устанавливает кратные (единица физической величины, в целое число раз большая системной и внесистемной единицы) и дольные(единица физической величины, в целое число раз меньшая системной или внесистемной единицы) (таблица 2.4).
Таблица 2.4 – Множители и приставки, используемые для образования наименований и обозначений десятичных кратных и дольных единиц
| Множитель | Приставка | Обозначение приставки | Множитель | Приставка | Обозначение приставки |
| экса | Э | деци | д | ||
| пета | П | санти | с | ||
| тера | Т | милли | м | ||
| гига | Г | микро | мк | ||
| мега | М | нано | н | ||
| кило | к | пико | п | ||
| гекто | г | фемто | ф | ||
| дека | да | атто | а |
Например, системная единица «метр» (м); кратная ей – «километр» (км), дольная – миллиметр «мм» (мм).
ТЕМА 3. ИЗМЕРЕНИЯ
3.1 Классификация измерений
Измерение физической величины– совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.
Измерения классифицируются по ряду признаков.
Признак 1.По общим приемам получения результатов измерений:
1) прямые –измерения, при которых искомое значение физической величины получают непосредственно. Примерами прямых измерений являются: измерения длины линейкой, т. е. путем сравнения искомой величины с мерой – линейкой и др.;
2) косвенные – измерения, при которых искомое значение величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Например, мощность электрической цепи постоянного тока в соответствии с формулой P = I·U можно определить, проведя прямые измерения силы тока и напряжения;
3) совокупные – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Пример: значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь;
4) совместные– проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними.
Признак 2. По отношению к изменению измеряемой величины:
1) статические – измерения физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Пример: измерение длины детали при нормальной температуре;
2) динамические – измерения изменяющейся по размеру физической величины.
Признак 3. По числу измерений:
1) однократные – измерения, выполненные один раз;
2) многократные – измерения физической величины одного и того же размера, результат которых получен из нескольких следующих друг за другом измерений, т. е. состоящие из ряда однократных измерений.
Признак 4. По способу выражения результатов измерений:
1) абсолютные – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Пример: измерение силы F = mg основано на измерении основной величины - массы m и использовании физической постоянной g (в точке измерения массы);
2) относительные – измерения отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную. Пример: измерение плотности жидкости ареометром;
Признак 5.По характеристике точности:
1) равноточные – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью;
2) неравноточные – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
Принципы измерений
Принцип измерений – это физическое явление или эффект, положенное в основу измерений. Рассмотрим лишь несколько широко распространенных эффектов.
1. Пьезоэлектрический эффект заключается в возникновении ЭДС на поверхности (гранях) некоторых кристаллов (кварц, турмалин, искусственные пьезоэлектрические материалы – пьезокерамики и др.) под действием внешних сил (сжатие, растяжение). Наибольшее применение для измерений нашли кварц и пьезокерамики (например, титанат бария), обладающие достаточно высокой механической прочностью и температурной стабильностью (кварц до температуры примерно 200 °С, пьезокерамика – до 115 °С). Пьезоэлектрический эффект обратим: ЭДС, приложенная к пьезоэлектрическому кристаллу, вызывает механические напряжения на их поверхности.
2. Термоэлектрический эффект широко применяется при измерениях температуры, причем используются две основных разновидности способов использования этого эффекта.
В первом используется свойство изменения электрического сопротивления металлов и полупроводников при изменении температуры. Из металлов часто применяются медь (для обычных измерений) и платина (для высокоточных измерений). Соответствующий измерительный преобразователь называется терморезистором. Чувствительные элементы полупроводникового преобразователя – термистора – изготавливаются из окислов различных металлов. С увеличением температуры сопротивление термистора уменьшается, в то время как у терморезистора – возрастает. Зависимость изменения сопротивления термисторов при изменении температуры существенно нелинейна, у медных терморезисторов – линейна, у платиновых аппроксимируется квадратным трехчленом. Платиновые терморезисторы позоляют измерять температуру в пределах от минус 200 до + 1000 °С.
Другим способом использования термоэлектрического эффекта является возникновение термо-ЭДС в замкнутом контуре, состоящем из двух разнородных проводников (или полупроводников), соединенных (спаянных) между собой на одном конце, а на другом подключенным к измерителю ЭДС, при различии температуры в месте спая и в месте соединения с измерителем. Соответствующие соединения двух разнородных проводников (полупроводников) называются термопарами. Широко используются для термопар хромель, копель, константан, платина и др. Термопары позволяют измерять температуру в широком диапазоне (от минус 200 до + 2800 °С). Например, пара хромель-константан позволяет измерять температуру до + 700 °С, а пара вольфрам-рений – до + 2800 °С. При этом приходится применять чувствительные измерители ЭДС, так как величина термо-ЭДС составляет от значений примерно 10 до 80 мкВ/°С.
3. Фотоэлектрический эффект. Для целей измерений используется внешний и внутренний фотоэффекты.
Внешний фотоэффект возникает в вакуумированном баллоне, имеющем анод и фотокатод. При освещении фотокатода в нем под влиянием фотонов света эмитируются электроны. В случае наличия между анодом и фотокатодом электрического напряжения эмитируемые фотокатодом электроны образуют электрический ток, называемый фототоком. Таким образом, происходит преобразование световой энергии в электрическую. Описанный преобразователь называется фотоэлементом. Существуют также газонаполненные фотоэлементы.
Внутренний фотоэффект возникает при освещении слоя между некоторыми полупроводниками и металлами. В этом слое возбуждается ЭДС. У ряда полупроводников под влиянием светового излучения изменяется электрическое сопротивление. Иногда этот эффект называется фоторезистивным, а соответствующие устройства – фоторезисторами. «Темновое» (при отсутствии освещения) сопротивление фоторезистора достаточно большое (например, 108 Ом). При освещении оно может уменьшиться до 105 Ом. Фоторезисторы обладают высокой чувствительностью, существенно превышающей чувствительность фотоэлементов. В качестве фоточувствительного материала применяют сернистый кадмий, сернистый свинец, кремний и др.
Методы измерений
Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений.
Методика выполнения измерений – установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов измерений с гарантированной точностью в соответствии с принятым методом.
Методы измерений делятся:
1) метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений;
2) метод сравнения с мерой– метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (пример: измерение массы на рычажных весах с уравновешиванием гирями (мерами массы с известным значением)). Методы сравнения реализуются следующими способами:
- дифференциальный метод измерений – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Точность этого метода может быть высокой и определяется точностью величины, воспроизводимой мерой. Характерным примером дифференциального метода, иногда называемого методом неполного уравновешивания, является приведенный на рисунке 3.1. Вольтметр V включается с помощью переключателя П в цепь с измеряемым сопротивлением rx или в цепь с регулируемым потенциометром (мерой) r0. При достижении одинаковых показаний вольтметра (rx = r0) регистрируется искомое значение rx;
- нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Характерным примером нулевого метода является измерение активного сопротивления мостом постоянного тока (рисунок 3.2).
|
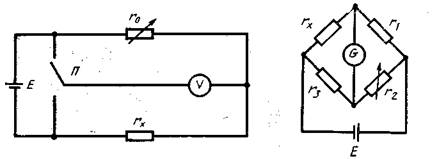
|
Мостовая схема оказывается полностью уравновешенной (гальванометр G показывает нуль), когда выполняется следующее условие: rxr2 = r1r3. Таким образом, при полном уравновешивании искомая величина rx = r1r3/r2;
- метод измерений замещением – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Пример: взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (метод Борда);
- метод совпадений – метод сравнения с мерой, в котором разность между измеряемой величиной и известной величиной, воспроизводимой мерой измеряют, используя совпадения отметок шкал. Пример: измерение с помощью штангенциркуля.
Дата добавления: 2016-03-27; просмотров: 2604;
