Иллюстрация симплекс-метода.

Лекции 2-3.

Рассмотрим идею симплекс-метода на простом примере:

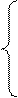x₂ + 2x₄ + 3x₅ – 7 = 0

x₃ – x₄ – 3x₅ – 2 = 0 (1)

x₁ + + x₄ + x₅ – 2 = 0

x₁, …,x ₅ ≥ 0

F = 3 – x₄ + x₅ → min (2)

Первые три столбца коэффициентов линейно независимы,образуют матрицу ранга 3

0 1 0

0 0 1

1 0 0 .

Поэтому соответствующие переменные x₁ , x₂ , x₃ можно взять в качестве базисных переменных. При этом x₄, x₅ – свободные переменные.

Заметим, что сведя эту задачу ЛП к стандартному виду с двумя переменными, легко решить ее геометрическим методом (будет рассмотрен на семинаре). Но у нас сейчас задача другая – рассмотреть идею симплекс-метода.

Итак, x₄ и x₅ - свободные переменные. Выразим через них базисные переменные:

x₁ = 2 – x₄ – x₅

x₂ = 7 – 2x₄ – 3x (3)

x₃ = 2 + x₄ + 3x₅ ,

а целевая функция в этом примере уже выражена через свободные переменные:

F = 3 – x₄ + x₅ → min.

Если целевая функция содержит и базисные переменные, исключаем их через (3).

Замечание. Запись (3) задает общее решение СЛУ (1): перебирая все значения свободных переменных x₄ и x₅, и вычисляя по формулам (3) соответствующие значения базисных переменных x₁ , x₂ , x₃, получим все решения СЛУ (1).

Положим x₄ = 0 и x₅ = 0, тогда из (3) x₁ = 2, x₂ = 7, x₃ = 2. Соответствующее базисное решение х⁽¹⁾ = (2, 7, 2, 0, 0) оказывается допустимым (неотрицательным), но, скорее всего, не оптимальным. Ему соответствует значение целевой функции F(x⁽¹⁾) = 3. Как перейти к другому допустимому базисному решению, улучшив также при этом значение целевой функции? Можно ли это сделать за счет изменения (увеличения от 0) x₄ или x₅? Глядя на целевую функцию (2), видим, что переменная x₅ входит в F с положительным коэффициентом, поэтому увеличивать ее нет смысла. А увеличение х₄ разумно, оно уменьшает F. До какого предела можно увеличивать х₄ (при фиксированном х₅=0)? Ведь рост этой переменной в соответствии с условиями (3) вызывает изменение базисных переменных и они в какой-то момент могут перестать быть неотрицательными.

Из ограничений-равенств (3) следует что:

x₁ < 0 при x₄ > 2 (минимальное значение !)

x₂ < 0 при x₄ > 3,5

x₃ > 0 при любых х₄ .

Вывод: Можно и нужно увеличивать х₄ до значения, равного 2 (при больших х₄, нарушается условие неотрицательности x₁ ), при этом получим (в силу (3)) решение:

x₁ = 0, x₂ = 3, x₃ = 4, x₄ = 2, x₅ = 0 или х⁽²⁾ = (0, 3, 4, 2, 0). Значение целевой функции улучшилось: F(x⁽²⁾) = 1<3= F(x⁽¹⁾).

В новом решении, как и в предыдущем, две нулевые компоненты. Попытаемся привести систему (1) к новому базису, в котором соответствующие переменные x₁ и x₅ будут свободными переменными (тогда можно будет убедиться, что x⁽²⁾ - базисное решение). Для этого выразим «новые» базисные переменные x₂, x₃ , x₄ через «новые» свободные переменные x₁ и x₅.

При этом, как говорят, переменная x₄ вводится в базис, а x₁ выводится из базиса.

Из первого уравнения в (3) выразим новую базисную переменную x₄:

x₄ = 2 – х₁ – х₅.

Заметим, что это именно то уравнение, которое «остановило» рост х₄ в (3). Исключим x₄, подставив это выражение для него в два других уравнения в (3) и в целевую функцию. Получим следующее представление системы ограничений в новом базисе (x₂, x₃ , x₄₎:

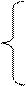x₂ = 3 + 2х₁ – х₅

x₃ = 4 – х₁ + 2х₅

x₄ = 2 – х₁ – х₅

F = 1 + x₁ +2x₅ → min

В новом базисном решении F(x⁽²⁾) = 1. Так как все коэффициенты целевой функции положительны, никакие допустимые изменения свободных переменных не уменьшают целевой функции. Таким образом, мы имеем в точке х⁽²⁾ = (0, 3, 4, 2, 0) оптимум (минимум).

Замечание. В этой задаче оптимальное решение найдено за один шаг (итерацию). Если в новом базисе целевая функция имела бы отрицательный коэффициент (при некоторой свободной переменной), следовало бы проделать вторую итерацию, аналогичную первой. Сходимость симплекс-метода следует из того, что число допустимых базисов конечно, не превосходит числа сочетаний из n (число всех переменных) по m (ранг системы ограничений-равенств). Однако полного перебора всех допустимых базисов не происходит, так как на каждой операции значение целевой функции улучшается и базисы, «худшие», чем текущий, в рассмотрение далее не попадают.

Резюме. Симплекс-метод состоит в переходе от одного допустимого базисного решения к другому, причем так, что на каждом шаге значение целевой функции улучшается. Он находит оптимальное решение за конечное число шагов (или устанавливает, что оптимума нет – задача несовместна или неограничена).

Лекция 3.

Пример: как перейти от базиса к базису

1)2x₁ + x₂ – x₃ = 3

x₁ + x₃ – x₄ = -2

3x₁ - x₃ + x₅ = 1

x₁ x₂ x₃ x₄ x₅ ∑

x₂ 2 1 -1 0 0 3 5

x₄ 1 0 2 1 0 -2 2

x₅ 3 0 -2 0 1 1 3

Соответственно базисное решение: (0, 3, 0, -2, 1). Перейдем к другому базису, введя в число базисных переменных х₃ и выведя х₄:

x₁ x₂ x₃ x₄ x₅ ∑

x₂ ⁵/₂ 1 0 ¹/₂ 0 2 6

x₃ ¹/₂ 0 1 ¹/₂ 0 -1 1

x₅ 4 0 0 1 1 -1 5

Новое базисное решение: (0, 2, -1, 0, -1)

2) Пусть был допустимый базис (x₂,x₄,x₃) и соответствующее базисное решение (0,2,3,1,0)

x₁ x₂ x₃ x₄ x₅ b ∑

²/₁ x₂ 1 1 0 0 -3 2 1

¹/₃ x₄ 3 0 0 1 1 1 6

x₃ 0 0 1 0 -2 3 2

Исходное базисное решение (0, 2, 3, 1, 0) и базис допустимы.

Введем х₁ в базис, выведя х₂.

x₁ x₂ x₃ x₄ x₅ b ∑

x₁ 1 1 0 0 -3 2 1

x₄ 0 -3 0 1 10 -5 9

x₃ 0 0 1 0 -2 3 2

Придем к недопустимому базису x⁽²⁾ = (2, 0, 3, -5, 0). Введение в базис переменной x₁ с выведением x₄ привело бы нас к допустимому базису

Как осуществить переход от допустимого к допустимому базису.

1. разрешающий столбец A^j (вводимый в базис) должен содержать хотя бы один положительный элемент a_ij > 0.
2. для всех положительных элементов этого столбца A^j надо подсчитать отношение b_i/a_ij и выбрать строку i, для которой оно минимум.