Цветовая система XYZ

В основу построения системы XYZ были положены следующие условия.

1. Удельные координаты - кривые смешения не должны иметь отрицательных ординат, т.е. все реальные цвета определяются положительными значениями модулей основных цветов выбранной координатной системы.

2. Количественная характеристика цвета - яркость - должна полностью определяться одним его компонентом.

3. Координаты белого цвета равноэнергетического излучения Е должны быть равными.

Для обеспечения данных требований в качестве основных цветов были выбраны три теоретических (реально не воспроизводимых) цвета XYZ. Координатная система XYZ выбрана так, чтобы векторы основных цветов находились в цветовом пространстве вне тела реальных цветов. Оси X, Y, Z являются ортогональной декартовой системой координат осей в цветовом пространстве - координата Y полностью определяется яркостью цвета, а два других основных цвета X и Z лежат в плоскости нулевой яркости.

Любой цвет в системе XYZ описывается следующим выражением:

fʹF=xʹX+yʹY+zʹZ

и изображается в цветовом пространстве точкой с координатами xʹ, yʹ, zʹ или вектором, проведенным в эту точку из начала координат. Модули основных цветов xʹ, yʹ, zʹ определяются выражениями, ана­логичными (4.5):

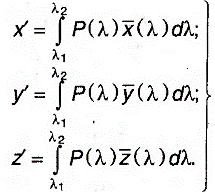
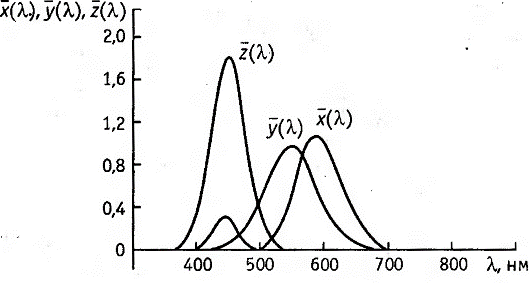
Рис. 4.8. Удельные координаты цвета в системе XYZ

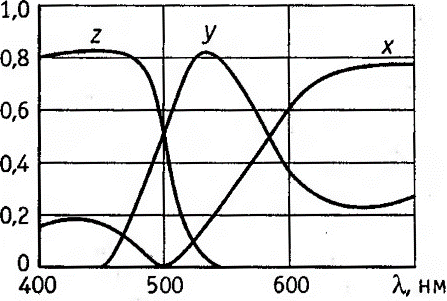
Рис. 4.9. Координаты цветности в системе XYZ

Графики удельных координат (кривые смешения) в системе XYZ показаны на рис. 4.8.

Координаты цветности чистых ^спектральных цветов х, у, z в системе XYZ вычислены и стандартизованы МКО. Например х=xʹ/M; у = у'/М; z=z'/М, где М = хʹ+yʹ+zʹ - модуль цвета. Значения координат цветности х, у, z для монохроматических излучений изображены графически на рис. 4.9.

В системе XYZ одна из координат цветности является зависимой от двух других, так как х+ у+ z= 1. Поэтому для определения цветности достаточно двух координат, например х и у.

Для практических расчетов в системе XYZ рекомендуется использовать известную диаграмму цветности МКО, полученную проекцией диаграммы цветности единичной плоскости на плоскость ху в направлении оси z (рис. 4.10).

Анализируя цветовой график МКО, необходимо отметить следующее.

1. Координаты цветности всех реальных цветов находятся внутри спектрального локуса (геометрического места координат цветности чистых спектральных цветов) и определяются положительными значениями х и у.

2. Равноэнергетический белый цвет E, имеющий чисто теоретический, расчетный характер, находится в центре тяжести треугольника хоу. Его координатами цветности будут х = 1/3 и у = 1/3.

3. Цветность смеси двух цветов отображается точкой, лежащей на прямой, соединяющей смешиваемые цвета.

4. Цветность смеси трех цветов отображается точкой внутри треугольника, вершины которого образованы смешиваемыми цветами.

Цветность сложного излучения помимо координат цветности может быть охарактеризована цветовым тоном и насыщенностью. Цветовой тон любого цвета на диаграмме цветности МКО определяется длиной волны монохроматического излучения (доминирующей длиной волны λ_d), соответствующей пересечению кривой спектральных цветов - спектрального локуса с прямой, проходящей через точку Е и точку, отображающую цветность искомого цвета, например точку М (см. рис. 4.10). Насыщенность численно характеризуется чистотой цвета Р_цв, т.е. относительным содержанием в нем спектрального цвета (монохроматического светового потока F_λ):

Р_цв=100 F_λ /( F_λ + F_б),%,

где F_б - световой поток белого цвета, входящего в смесь со спектральным цветом.

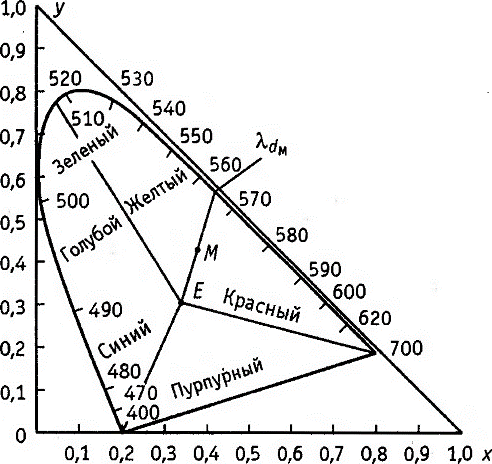
Рис. 4.10. Диаграмма цветности МКО

Насыщенность максимальна (Р_цв = 100%) для чистых спектраль­ных и пурпурных цветов и минимальна (Р_цв = 0) для белого цвета.