Примем следующий порядок расчета.
1. Разлагаем все внешние силы на составляющие
P1x, P2x,..., Pnx и P1y, P2y,..., Pny.
2. Строим эпюры изгибающих моментов My и My. от этих групп сил.
У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента Mx, и My а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис. 2)
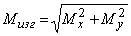 ,
,
который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору Мизг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру Мизг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

Рис.2. Формирование результирующего изгибающего момента
3. Строится эпюра крутящего момента Мz.
Наибольшие напряжения изгиба возникают в точках k и k/, наиболее удаленных от нейтральной оси (рис. 3),
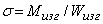 .
.
где Wизг — момент сопротивления при изгибе.
В этих же точках имеют место и наибольшие касательные напряжения кручения
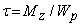 ,
,
где Wр— момент сопротивления при кручении.
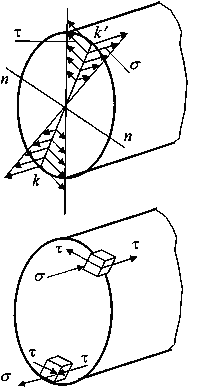
а) эпюры напряжений б) распределение напряжений
Рис.3. Напряженное состояние вала:
Как следует из рис. 3, напряженное состояние является упрощенным плоским (сочетание одноосного растяжения и чистого сдвига). Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по критерию Треска—Сен-Венана имеем
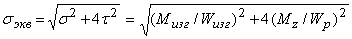 .
.
Учитывая, что Wр=2 Wизг, для эквивалентных напряжений получаем
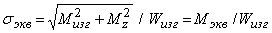 ,
,
где 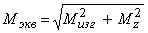 —эквивалентный момент, с введением которого задача расчета вала на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.
—эквивалентный момент, с введением которого задача расчета вала на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.
Аналогично для Мэкв по.критерию Губера—Мизеса получаем
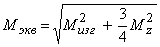
Тогда условие прочности для вала из пластичного материала будет иметь вид
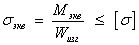 .
.
Для стержня из хрупкого материала условие прочности следует записать в виде
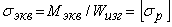 ,
,
где Мэкв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора
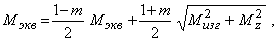
где 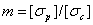 .
.
Обратим внимание на особенности расчета при сочетании изгиба, растяжения и кручения стержня прямоугольного поперечного сечения (рис. 4.) Для выявления опасной точки здесь должны быть сравнены напряжения косого изгиба с растяжением в точке А, с эквивалентными напряжениями в точках В и С.
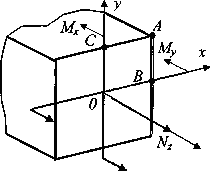
Рис.4. Модель расчета напряжений при сочетании кручения, растяжения и изгиба.
Полученные соотношения приобретают крайнюю необходимость и востребованность при выполнении Вами курсового проекта по основам конструирования при расчете на прочность и жесткость валов передач.
Лекция № 30. Расчет балок переменного сечения.
Дата добавления: 2016-03-05; просмотров: 673;
