Цепи переменного тока
Рассмотрим в цепи переменного тока произвольный блок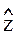 
, который может содержать в общем случае резисторы, индуктивности, емкости.
Модуль импеданса определяет отношение действительных амплитуд напряжения и тока
½ 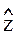½= U0 / I0, (7)
а аргумент импеданса определяет фазовый сдвиг тока и напряжения
arg 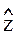= Dj . (8)
Найдем напряжение, создаваемое источником тока на резисторе, индуктивности и емкости:
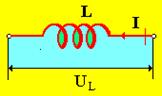
| Рис. 3 |
|
1. Напряжение, создаваемое источником тока на индуктивности (рис.3), равно взятой с обратным знаком ЭДС самоиндукции
UL = L dI/dt.
Импеданс индуктивности найдем по формуле
½ 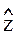½= wL.
Аргумент импеданса индуктивности можно найти по формуле
arg 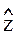L = p/2.
Следовательно, на индуктивности напряжение на четверть периода опережает ток.
| Рис. 4 |
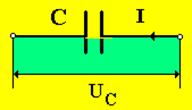
1. Напряжение, создаваемое источником тока на конденсаторе (рис.6.4)
|
Uс = q / C. (9)
Импеданс емкости найдем по формуле
½ 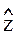½= 1 / wC. (10)
Аргумент импеданса емкости можно найти по формуле
arg 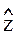С = - p/2. (11)
2. Напряжение, создаваемое источником тока на активном сопротивлении (рис. 5)
UR = IR. (12)
| Рис. 5 |
|
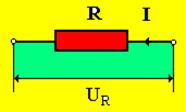
Импеданс активного сопротивления действителен
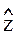= R,
поэтому фаза тока и напряжения совпадают.
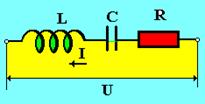
3. Найдем напряжение, создаваемое источником тока в цепи, содержащей резистор, индуктивность и емкость (рис. 6).
Ипеданс этой цепи
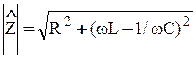. (13)
| Рис. 6 |
Аргумент импеданса
|
arg 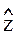= Dj = arctg{[wL - 1/(wC)]}/R. (6.14)
Таким образом, действительную амплитуду тока можно найти по формуле
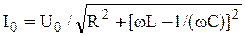. (15)
Активную мощность на участке цепи переменного тока можно найти по формуле
Pa = <P> = IUcosj/2. (16)
Замечание: в отличие от активного сопротивления, где происходит диссипативное преобразование энергии электрического тока в ленц-джоулево тепло, в индуктивности и емкости наблюдается без диссипативное преобразование энергии тока в энергию магнитного и электрического полей с последующим обратным превращением в энергию тока.
Дата добавления: 2016-02-09; просмотров: 615;