Резонансные контуры в усилительных схемах
Основными характеристиками колебательных контуров являются: резонансная частота ω0, характеристическое сопротивление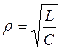 
, добротность Q. На резонансной частоте 
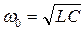последовательный колебательный контур имеет низкое эквивалентное резонансное сопротивление rОЭ, а параллельный колебательный контур – высокое RОЭ.
На частотах ниже ω0 сопротивление последовательного колебательного контура носит емкостный характер, а при переходе через резонансную частоту – индуктивный. В параллельном колебательном контуре все наоборот.
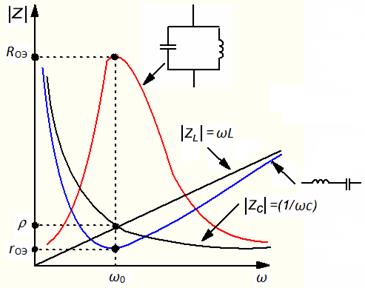
Рис. 9.12. Частотные свойства контуров Z = f(ω), имеющих одинаковые величины L и С
Собственная добротность контура Q0, с одной стороны, определяется как отношение значения f0 = 2πω0 к полосе пропускания Δf на уровне –3 дБ: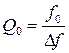 
. С другой стороны, 
.
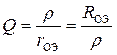Собственная добротность резонансного контура характеризуется в основном добротностью катушки индуктивности QL, которая и будет определять добротность колебательного контура, т.е. Q = QL.
При расчетах резонансных цепей необходимо учитывать условие оптимального согласования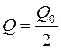 
, которое исходит из компромисса между величиной добротности Q и КПД контура. КПД возрастает при увеличении вносимого в контур сопротивления rВН (нагрузки) с целью съема полезного сигнала, однако при этом ухудшается добротность. Условие оптимального согласования предполагает для параллельного контура RВН = RОЭ/2, а для последовательного – rВН = 2rОЭ.
Рассмотрим несколько транзисторных схем с использованием колебательных контуров. Данные схемы обладают выраженными резонансными свойствами и позволяют осуществлять усиление (селекцию) сигнала или, наоборот, его подавление (режекцию) вблизи частоты ω0.
В резонансном усилителе (рис. 9.13) в качестве коллекторной нагрузки используется колебательный контур, имеющий высокое эквивалентное сопротивление RОЭ на частоте ω0. Коэффициент усиления данного резонансного усилителя равен: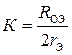 
.
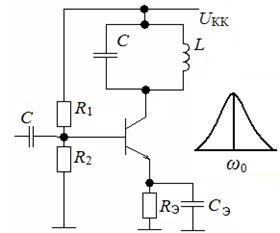
Рис. 9.13. Резонансный усилитель с параллельным колебательным контуром
в качестве коллекторной нагрузки
На входе усилителя с ОЭ (рис. 9.14) поставлен так называемый фильтр-пробка, который имеет высокое RОЭ и не пропускает часть сигнала вблизи ω0.
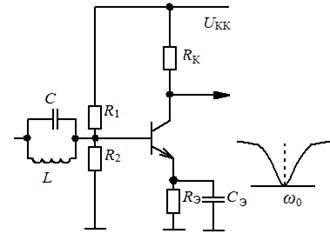
Рис. 9.14. Фильтр-пробка на входе усилителя
Параллельный колебательный контур в эмиттерной цепи (рис. 9.15) резко снижает усиление сигнала вблизи ω0, поскольку для такого усилителя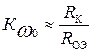 
. Для других частот 
.
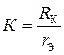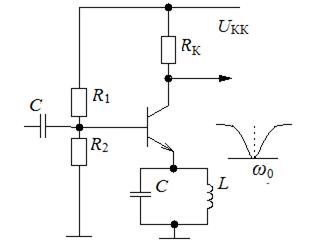
Рис. 9.15. Резонансный усилитель с параллельным колебательным контуром
в качестве эмиттерной нагрузки
В схеме на рис. 9.16 осуществляется коррекция (дополнительное усиление) сигнала вблизи частот ω0, так как RЭ шунтировано последовательным контуром, имеющим малое rОЭ. При коррекции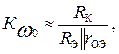 
на других частотах сигнала 
.
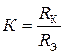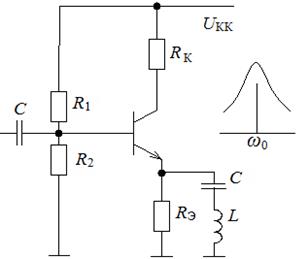
Рис. 9.16. Резонансный усилитель с последовательным колебательным контуром,
шунтирующим эмиттерный резистор
Контрольные вопросы к лекции
1. Какие недостатки простейшей схемы пикового детектора и за счет чего можно устранить при использовании ОУ?
2. Какими достоинствами обладает ЦАП на ОУ с матрицей R-2R по сравнению со схемой ЦАП на основе суммирующего ОУ?
3. За счет чего достигается усиление мощности с схемах на основе ОУ?
4. Каким образом ООС влияет на входное сопротивление инвертирующего ОУ?
5. Каким образом ООС влияет на входное сопротивление неинвертирующего ОУ?
6. Каким образом ООС влияет на выходное сопротивление инвертирующего ОУ?
7. Каким образом ООС влияет на выходное сопротивление неинвертирующего ОУ?
8. Какие параметры резонансного контура необходимо учитывать при проектировании резонансных усилителей?
ЛЕКЦИЯ 10
Дата добавления: 2016-02-02; просмотров: 1731;