ОСМОС и ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ.
Двухкомпонентные растворы, один из компонентов которого нелетуч.
Рассмотрим бесконечно разбавленные растворы нелетучих веществ.
ЭБУЛЛИОСКОПИЯ.
Рассмотрим раствор сахара в воде, который подчиняется закону Рауля.
Сахар является нелетучим компонентом, поэтому над раствором есть только насыщенный пар воды p 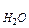 . Давление этого насыщенного пара меньше, чем давление насыщенного пара воды над чистой водой и определяется по закону Рауля:
. Давление этого насыщенного пара меньше, чем давление насыщенного пара воды над чистой водой и определяется по закону Рауля:
p 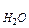 = p
= p 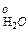
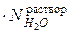 ; p
; p 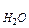 < p
< p 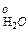
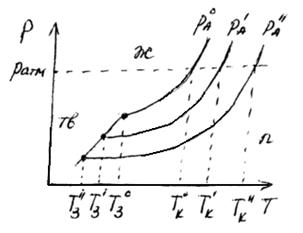
Зависимость давления насыщенного пара над разбавленным раствором или над чистым растворителем от температуры можно отобразить графически:
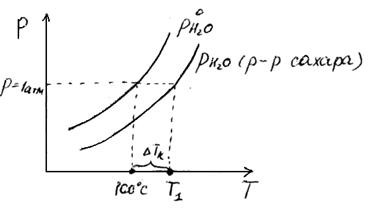
Известно, что любая жидкость закипает тогда (при такой температуре), когда давление насыщенного пара становится равным внешнему давлению.
Таким образом, температура кипения – это та температура, при которой давление насыщенного пара жидкости становится равным внешнему давлению.
Рассмотрим чистую воду, которая при нормальном давлении в 1 атмосферу будет кипеть при t=100 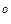 C (373 К).
C (373 К).
Очевидно, что раствор сахара в воде будет кипеть при более высокой температуре при том же давлении (1 атм.). Это мы можем показать графически, продолжив прямую, параллельную оси абсцисс до пересечения кривой зависимости давления насыщенного пара над раствором. Опустив перпендикуляр из этой точки на ось абсцисс, получим температуру кипения раствора сахара при давлении 1 атм (Т 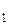 ).
).
Все растворы нелетучих веществ кипят при более высокой температуре, чем чистый растворитель.
Повышение температуры кипения раствора 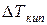 определяется как разность между температурой кипения раствора Т
определяется как разность между температурой кипения раствора Т 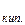 и температурой кипения чистого растворителя
и температурой кипения чистого растворителя 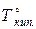 :
:
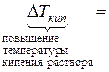

(для раствора сахара в воде 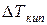 = Т
= Т 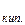 -100).
-100).
Повышение температуры кипения в зависимости от свойств раствора можно количественно определить двумя способами :на основе термодинамических представлений и из фазовых диаграмм состояния. Рассмотрим эти два способа.
Первый способ образуется на использовании уравнений химического потенциала 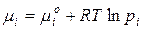 и уравнения Клапейрона–Клаузиуса
и уравнения Клапейрона–Клаузиуса
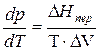 .
.
После соответсвуюәих преоразований из этих уравнений получим:
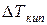 =
= 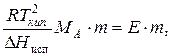 где
где
 – мольная энтальпия испарения растворителя;
– мольная энтальпия испарения растворителя;
 – молярная масса растворителя;
– молярная масса растворителя;
m – моляльность раствора, т.е. моляльная концентрация растворенного вещества (количество молей растворенного вещества в 1000 г растворителя);
Е – эбуллиоскопическая постоянная  .
.
То же выражение можно получить, рассматривая диаграммы состояния.
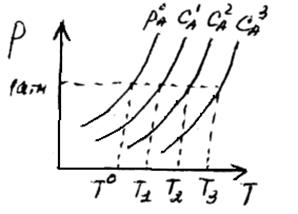
Для бесконечно разбавленного раствора и бесконечно малых участков кривых можно считать, что эти участки прямолинейны. Отсюда следует, что повышение температуры кипения пропорционально давлению насыщенного пара, которое в свою очередь определяется концентрацией растворенного вещества. Иными словами, повышение температуры кипения пропорционально концентрации растворенного вещества, что и выражает уравнение.
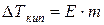
Эбуллиоскопическая постоянная Е зависит только от природы растворителя и не зависит от растворенного вещества.
Когда моляльная концентрация вещества равна единице (m= 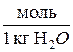 ), то получим
), то получим 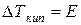 , то есть эбуллиоскопическая постоянная одномоляльного раствора равна повышению температуры кипения (
, то есть эбуллиоскопическая постоянная одномоляльного раствора равна повышению температуры кипения (  ), если этот раствор рассматривать как бесконечно разбавленный.
), если этот раствор рассматривать как бесконечно разбавленный.
Пример. Определить температуру кипения водного раствора, содержащего 3 г глюкозы (С 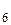 Н
Н 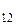 О
О 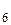 ) в 100 см
) в 100 см  воды. Молярная масса глюкозы
воды. Молярная масса глюкозы 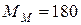 г/м, эбулиоскопическая постоянная воды Е
г/м, эбулиоскопическая постоянная воды Е 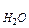 =0,52 (К
=0,52 (К 
Решение: т.к. плотность воды Р 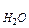 =1 г/см
=1 г/см  , то масса воды 100 г.
, то масса воды 100 г.
В 100 г воды растворено 3 г глюкозы.
В 1000 г воды растворено 30 г глюкозы.
Число молей глюкозы равно:
n= 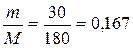 (моль).
(моль).
Тогда моляльность глюкозы : m= 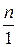 =0,167 моль/кг.
=0,167 моль/кг.
Повышение температуры кипения равно:
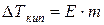 =0,52
=0,52 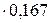 =0,087 K (
=0,087 K ( 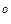 C)
C)
Тогда температура кипения раствора глюкозы равна:
T 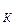 =T
=T 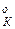 +
+ 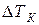 =100+0,087=100,087
=100+0,087=100,087 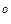 C
C
Определение молекулярной массы растворенного вещества.
Пусть в G г растворителя растворено g г нелетучего вещества с молекулярной массой 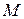 .
.
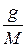 – число молей вещества.
– число молей вещества.
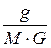 – число молей в G г растворителя.
– число молей в G г растворителя.
Тогда моляльность этого вещества в растворе:
M= 
Подставим это уравнение в уравнение 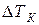 :
: 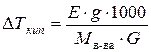 . Из этого уравнения можно выразить молекулярную массу растворенного вещества:
. Из этого уравнения можно выразить молекулярную массу растворенного вещества: 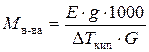 . Обычно эбуллиоскопическую постоянную Е определяют из справочника, а
. Обычно эбуллиоскопическую постоянную Е определяют из справочника, а 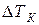 -экспериментально.
-экспериментально.
Определение молекулярной массы растворенного вещества по повышению температуры кипения называется эбуллиоскопией и относится к физико–химическим методам анализа.
КРИОСКОПИЯ.
Из опыта известно, что температура замерзания растворов ниже, чем чистого растворителя. Вспомним хотя бы зимние улицы, когда после посыпания их солью образуется раствор, который не замерзает при минусовой температуре.
Понижение температуры замерзания также можно определить графически.
Понижение температуры замерзания раствора объясняется тем, что растворенное вещество препятствует кристаллизации растворителя, т.е. его переходу из жидкого в твердое состояние.
Понижение температуры замерзания определяется как разность между температурой замерзания растворителя и температурой замерзания раствора:
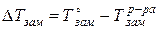
По аналогии с определением повышения температуры кипения находят понижение температуры замерзания раствора:
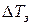 =
= 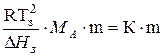 , где
, где
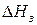 – мольная энтальпия замерзания (плавления) растворителя;
– мольная энтальпия замерзания (плавления) растворителя;
Т 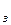 – температура замерзания растворителя;
– температура замерзания растворителя;
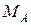 – молярная масса растворителя;
– молярная масса растворителя;
К – криоскопическая постоянная  .
.
К 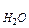 =1,86 К∙кг/моль
=1,86 К∙кг/моль
С помощью измерений понижения температуры замерзания можно определить молярную массу растворенного вещества по формуле:
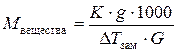 – для растворов неэлектролитов
– для растворов неэлектролитов
g – масса растворенного вещества (в граммах);
G – масса растворителя (в граммах).
Этот метод определения молекулярной массы растворенного вещества называется криоскопией.
В связи с тем, что экспериментально легче определить понижение температуры замерзания раствора, предпочтение отдается определению молекулярной массы растворенного вещества методом криоскопии.
Пример. Определим молекулярную массу С 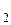 Н
Н 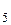 ОН водного раствора этилового спирта, содержащего 8,74 г спирта на 1000 г воды, если раствор замерзает при температуре -0,354
ОН водного раствора этилового спирта, содержащего 8,74 г спирта на 1000 г воды, если раствор замерзает при температуре -0,354 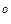 С, а криоскопическая постоянная для воды равна 1,86
С, а криоскопическая постоянная для воды равна 1,86  .
.
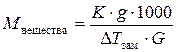 =
= 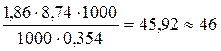 г/моль
г/моль
Определим температуру замерзания водного раствора, содержащего 30 г глюкозы ( 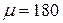 г/моль) и 50 г воды.
г/моль) и 50 г воды.
В соответствии с формулой 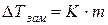 , определим моляльную концентрацию глюкозы :
, определим моляльную концентрацию глюкозы :
m= 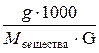 =
=  =3,33 моль/кг
=3,33 моль/кг
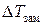 =1,86∙3,33=6,3
=1,86∙3,33=6,3 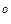 С
С
Температура замерзания раствора :
T 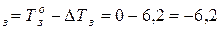
 C
C
Повышение температуры кипения и понижение температуры замерзания являются коллигативными свойствами растворов.
ОСМОС и ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ.
К коллигативным свойствам растворов относятся осмос и вызываемое им осмотическое давление.
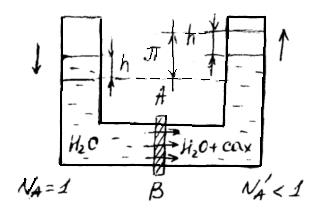
В сосуд, разделенный полунепроницаемой перегородкой АВ (мембраной) с одной стороны помещен раствор сахара в воде, с другой стороны чистая вода (растворитель).
Полунепроницаемая перегородка АВ пропускает в обе стороны молекулы воды, но не пропускает молекулы растворенного вещества (сахар). Примером полунепроницаемой перегородки может быть бычий пузырь.
Концентрация растворителя (вода) по обе стороны полунепроницаемой перегородки будет неодинакова. В правой части сосуда некоторый объем занимают молекулы растворенного вещества и концентрация растворителя будет меньше, чем в левой части сосуда с чистым растворителем. Растворитель из области более высокой концентрации самопроизвольно будет перемещаться в область с меньшей концентрацией, т.е. из левой части сосуда в правую. Это перемещение называют осмосом, которое на рис. покажем стрелками.
Осмос – это самопроизвольный процесс перехода растворителя через полунепроницаемую перегородку (мембрану) из растворителя в раствор или из менее концентрированного раствора в более концентрированный.
При переходе воды из левой части сосуда в правую, в этой части сосуда будет увеличиваться уровень жидкости на величину h. Одновременно на эту же величину h уровень жидкости в левой части сосуда понизится. Разность между уровнями жидкости в левом и правом коленах, при которой прекращается переход растворителя, определяет величину осмотического давления.
Осмотическое давление можно выразить следующим образом:
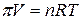 – уравнение Вант-Гоффа, где
– уравнение Вант-Гоффа, где
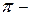 осмотическое давление; n – число молей растворенного вещества.
осмотическое давление; n – число молей растворенного вещества.
Это уравнение по имени автора называется уравнением Вант-Гоффа.
Для молярной концентрации (С=n/V):
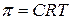
Уравнение Вант-Гоффа показывает, что осмос и вызванное им осмотическое давление зависят только от количества растворенного вещества, а не от его природы (коллигативные свойства).
Уравнение Вант-Гоффа напоминает уравнение состояния идеального газа pV=nRT. Подобное совпадение не случайно – оба уравнения отражают фундаментальное сходство систем на молекулярном уровне. В условиях равновесия осмотической системы растворенное вещество аналогично атомам идеального газа. Растворитель является лишь носителем растворенного вещества подобно роли вакуума для идеального газа.
Уравнение Вант-Гоффа позволяет рассчитать осмотическое давление, которое численно равно избыточному внешнему давлению, которое следует приложить к раствору, чтобы предотвратить осмос и восстановить одинаковый уровень жидкости раствора и растворителя, разделенных между собой полунепроницаемой перегородкой.
Пример. Рассчитать осмотическое давление 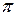 водного раствора, содержащего g=68,4 г сахарозы (
водного раствора, содержащего g=68,4 г сахарозы ( 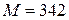 г/моль) и 1000 г воды, плотность раствора при t=20
г/моль) и 1000 г воды, плотность раствора при t=20 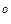 C
C 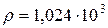 кг/м
кг/м  .
.
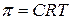 =
= 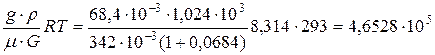 Па=4 атм.
Па=4 атм.
Осмос и осмотическое давление играют существенную роль в жизни растений и живых организмов. Так, оболочка клеток выполняет роль полупроницаемой мембраны.
Изотонический коэффициент i (коэффициент Вант-Гоффа).
Мы показали, что повышение температуры кипения определяется уравнением:
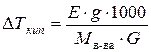
Отсюда молекулярная масса растворенного вещества:
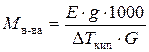
Для многих случаев экспериментальная молярная масса практически равна истинной молярной массе.
Но в ряде случаев экспериментальная молярная масса очень сильно отличается от истинной. Дело в том, что эти эффекты пропорциональны числу растворенных частиц.
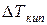 =
= 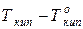
Например, при растворении сахара в растворе есть одна частица сахара С 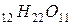 ,
,
сахар 1 частица С 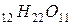
а при растворении KCl образуются две частицы KCl
2 частицы KCl 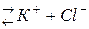
Т.к. 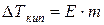 , где m-моляльная концентрация растворенного вещества. В этом случае нужно учесть образование двух частиц при растворении KCl.
, где m-моляльная концентрация растворенного вещества. В этом случае нужно учесть образование двух частиц при растворении KCl.
В случае электролитов вводится понятие изотонического коэффициента (коэффицента Вант–Гоффа i), который показывает, во сколько раз увеличивается число частиц в растворе в результате диссоциации.
В общем случае изотонический коэффициент равен:
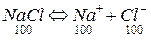 i=2
i=2
Na 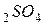
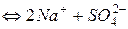 i=3
i=3
Однако при растворении не все молекулы электролита распадаются на ионы, оценивается степенью электролитической диссоциации, или просто степенью диссоциации, которую обычно обозначают 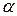 .
.
Пусть растворили N молекул вещества степень диссоциации равна:
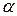 =
= 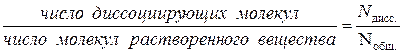
Тогда число продиссоциировавших молекул:
N 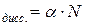
Неподвергшихся диссоциации молекул в растворе:
N 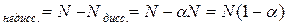
Пусть при диссоциации одной молекулы образуется 2 иона (обозначим число ионов, на которые распадается молекула через 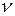 ).Тогда число ионов равно:
).Тогда число ионов равно:
N 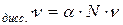
Число растворенных частиц = N 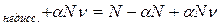
Тогда изотонический коэффициент равен
i = 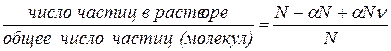
i = 1- 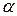 +
+ 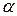
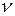
i = 1+ 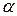 (
( 
Пример. Пусть хлорид натрия неполностью диссоциирует на ионы:
 ;
; 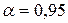 ;
; 
Тогда изотонический коэффициент равен:
i=1+ 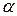 (
(  =1+0,95(2-1)=1,95
=1+0,95(2-1)=1,95
Изотонический коэффициент характеризует такие коллигативные свойства растворов электролитов, как повышение температуры кипения, понижение температуры замерзания, осмотическое давление и давление пара растворителя над раствором.
Для растворов электролитов повышение температуры кипения и понижение температуры замерзания будут описываться следующими выражениями:
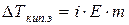 ;
;  ,
,
где m – моляльность раствора.
На основании вышеприведенных формул можно вывести формулу для определения истинной молярной массы вещества:
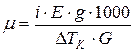 или
или
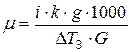
Однако, при отделении молярной массы растворенного вещества большое значение имеет выбор растворителя.
Например, криоскопическим методом определили молярную массу уксусной кислоты. В водном растворе молярная масса  г/моль, что полностью соответствует формуле. В растворе бензола молярная масса уксусной кислоты равна
г/моль, что полностью соответствует формуле. В растворе бензола молярная масса уксусной кислоты равна 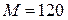 г/моль. Это указывает на существование в растворе молекул (СН
г/моль. Это указывает на существование в растворе молекул (СН 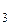 СООН)
СООН) 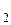 .Действительно, в бензоле между молекулами уксусной кислоты образуется водородная свзяь:
.Действительно, в бензоле между молекулами уксусной кислоты образуется водородная свзяь:
CH 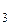 -C
-C 
В воде это невозможно, т.к. вода сама образует водородные связи:
CH 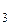 -C
-C 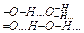
Дата добавления: 2016-02-02; просмотров: 3101;
