Глава IV. Простейшие случаи движения микрочастиц.
§ 4.1. Свободное движение частиц.
Рассмотрим свободное движение частицы, то есть такое движение, при котором на частицу не действуют внешние силы. Исходя из определения, ясно, что потенциальная энергия частицы равна нулю, так как потенциальная энергия есть энергия взаимодействия, а при его отсутствии она, очевидно, равна нулю. Тогда в операторе Гамильтона останется лишь слагаемое, описывающее её кинетическую энергию. В классической механике кинетическая энергия системы или частицы описывается следующим выражением: 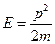 . В квантовой же механике эту величину описывает оператор Гамильтона. Для одномерного случая:
. В квантовой же механике эту величину описывает оператор Гамильтона. Для одномерного случая: 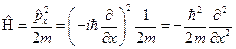 (1). Уравнение частицы описывается уравнением Шредингера:
(1). Уравнение частицы описывается уравнением Шредингера:  . Подставляя в него (1), получим:
. Подставляя в него (1), получим: 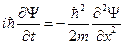 или
или 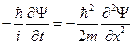 . В большинстве случаев движущейся частице можно поставить в соответствие волну де Бройля, поэтому мы можем выбрать волновую функцию, описывающую плоскую волну:
. В большинстве случаев движущейся частице можно поставить в соответствие волну де Бройля, поэтому мы можем выбрать волновую функцию, описывающую плоскую волну: 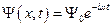 , где
, где  . Таким образом,
. Таким образом, 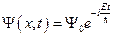 . Подставим этот вид волновой функции в уравнение Шредингера:
. Подставим этот вид волновой функции в уравнение Шредингера: 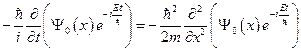 . Дифференцируя, вынося из-под знака дифференциала константы, и сокращая одинаковые множители, получим:
. Дифференцируя, вынося из-под знака дифференциала константы, и сокращая одинаковые множители, получим:  . В итоге, получим:
. В итоге, получим: 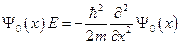 . Приведём полученное дифференциальное уравнение к стандартному виду:
. Приведём полученное дифференциальное уравнение к стандартному виду:  . Итак, мы получили дифференциальное уравнение второго порядка, независящее от времени. Оно называется стационарным уравнением Шредингера. Решая его, получим:
. Итак, мы получили дифференциальное уравнение второго порядка, независящее от времени. Оно называется стационарным уравнением Шредингера. Решая его, получим: 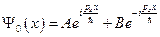 (2). Мы можем так записать, так как
(2). Мы можем так записать, так как 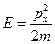 и, следовательно,
и, следовательно, 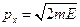 . Первое слагаемое в выражении (2) описывает движение частицы в направлении оси
. Первое слагаемое в выражении (2) описывает движение частицы в направлении оси  , а второе – против направления этой координатной оси. Итак, в общем случае:
, а второе – против направления этой координатной оси. Итак, в общем случае: 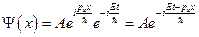 . Таким образом, общее уравнение Шредингера имеет однозначное и непрерывное решение, которое существует для любых значений
. Таким образом, общее уравнение Шредингера имеет однозначное и непрерывное решение, которое существует для любых значений  , что означает, что энергия свободно движущейся частицы может принимать любые значения, то есть энергетический спектр непрерывен. Более того, энергия частицы и её импульс являются величинами одновременно измеримыми, то есть
, что означает, что энергия свободно движущейся частицы может принимать любые значения, то есть энергетический спектр непрерывен. Более того, энергия частицы и её импульс являются величинами одновременно измеримыми, то есть  .
.
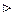 Доказательство. Так как по определению
Доказательство. Так как по определению  , то вычислим входящие в эту формулу слагаемые по очереди.
, то вычислим входящие в эту формулу слагаемые по очереди.
1.  . Воздействуем этим оператором на некоторую функцию
. Воздействуем этим оператором на некоторую функцию  :
:  . Таким образом,
. Таким образом,  .
.
2.  . Аналогично предыдущему пункту:
. Аналогично предыдущему пункту:  . Итак,
. Итак, 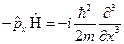 .
.
Находя теперь сумму слагаемых, полученных в пунктах 1 и 2, получим: 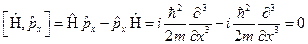 , что и требовалось доказать.
, что и требовалось доказать. 
Так как спектр собственных значений энергии непрерывен, то нормировка волновой функции оператора энергии на единицу невозможна. Действительно: 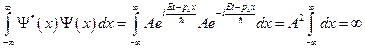 . Поэтому пользуются условием нормировки на длину периодичности. Этот способ состоит в следующем. Пусть само по себе движение частицы неограничено, но нас интересует движение частицы на участке
. Поэтому пользуются условием нормировки на длину периодичности. Этот способ состоит в следующем. Пусть само по себе движение частицы неограничено, но нас интересует движение частицы на участке 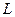 . В этом случае мы можем рассматривать не всё бесконечное пространство, а участок длиной
. В этом случае мы можем рассматривать не всё бесконечное пространство, а участок длиной 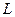 . Пусть вне этого участка значения волновой функции повторяются, то есть волновая функция периодична с периодом
. Пусть вне этого участка значения волновой функции повторяются, то есть волновая функция периодична с периодом 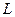 . Условие периодичности мы можем записать в виде:
. Условие периодичности мы можем записать в виде:  . Так как движение ограничено, то спектр энергии может быть дискретен. Найдём все возможные значения энергии:
. Так как движение ограничено, то спектр энергии может быть дискретен. Найдём все возможные значения энергии:  . Условие периодичности нам даёт следующее выражение:
. Условие периодичности нам даёт следующее выражение:  . Очевидно, что данное равенство возможно, если
. Очевидно, что данное равенство возможно, если 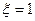 . Распишем эту экспоненту:
. Распишем эту экспоненту:  . Отсюда
. Отсюда 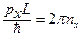 ,
, 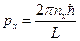 . Таким образом, импульс принимает какие-то строго определённые значения, значит, и энергия тоже принимает определённые дискретные значения:
. Таким образом, импульс принимает какие-то строго определённые значения, значит, и энергия тоже принимает определённые дискретные значения: 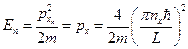 .
. 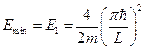 . Величина
. Величина  называется шагом дискретизации энергии. Найдём расстояние между энергетическими уровнями:
называется шагом дискретизации энергии. Найдём расстояние между энергетическими уровнями: 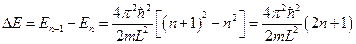 . Из последней формулы видно, что расстояния между энергетическими уровнями обратно пропорциональны
. Из последней формулы видно, что расстояния между энергетическими уровнями обратно пропорциональны  . Таким образом, чем конкретнее и меньше
. Таким образом, чем конкретнее и меньше 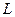 , тем разрежённей энергетические уровни. При
, тем разрежённей энергетические уровни. При 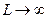 спектр, очевидно, становится непрерывным. Обобщая предыдущие рассуждения, можно сказать: чем точнее локализовано положение частицы. Тем ярче выражена дискретность её спектра.
спектр, очевидно, становится непрерывным. Обобщая предыдущие рассуждения, можно сказать: чем точнее локализовано положение частицы. Тем ярче выражена дискретность её спектра.
Воспользуемся для дискретного спектра условием ортонормированности волновой функции: 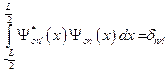 . Подставляя в него конкретные функции, получим:
. Подставляя в него конкретные функции, получим: 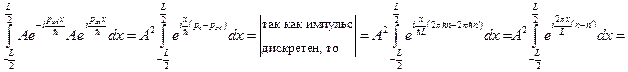
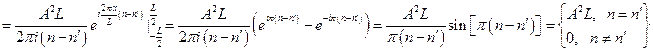 . Таким образом, чтобы выполнялось условие нормировки, необходимо положить
. Таким образом, чтобы выполнялось условие нормировки, необходимо положить 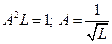 . Тогда система ортонормированных функций будет выглядеть так:
. Тогда система ортонормированных функций будет выглядеть так: 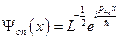 , где
, где 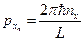 . Если перейти к волновому вектору
. Если перейти к волновому вектору 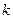 , то получим: так как
, то получим: так как  , то
, то 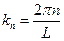 . И в выражении для волновой функции имеем:
. И в выражении для волновой функции имеем:  . Таким образом, мы нашли возможные значения энергии и волновой функции в случае ограниченного движения частицы по длине периода.
. Таким образом, мы нашли возможные значения энергии и волновой функции в случае ограниченного движения частицы по длине периода.
§ 4.2. Частица в одномерной потенциальной яме.
 Мы будем рассматривать связанное движение частиц. Движение частицы в потенциальной яме является примером такого движения. Потенциальной ямой называется область пространства, в которой потенциальная энергия меньше, чем в окружающем пространстве. В частности движение электрона в кулоновском потенциале ядра есть движение в потенциальной яме. Рассмотрим простейший случай одномерной потенциальной ямы с бесконечно
Мы будем рассматривать связанное движение частиц. Движение частицы в потенциальной яме является примером такого движения. Потенциальной ямой называется область пространства, в которой потенциальная энергия меньше, чем в окружающем пространстве. В частности движение электрона в кулоновском потенциале ядра есть движение в потенциальной яме. Рассмотрим простейший случай одномерной потенциальной ямы с бесконечно  высокими стенками. Её можно описать следующими уравнениями:
высокими стенками. Её можно описать следующими уравнениями: 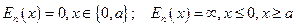 . Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы:
. Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы: 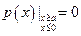 . Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и
. Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и  . Таким образом имеет смысл искать волновую функцию только внутри ямы. Стационарное уравнение Шредингера внутри ямы имеет вид:
. Таким образом имеет смысл искать волновую функцию только внутри ямы. Стационарное уравнение Шредингера внутри ямы имеет вид: 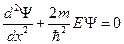 . Здесь
. Здесь  – энергия частицы. Запишем граничные условия:
– энергия частицы. Запишем граничные условия: 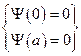 (1). Введём следующее обозначение:
(1). Введём следующее обозначение: 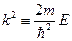 . Тогда уравнение Шредингера примет вид:
. Тогда уравнение Шредингера примет вид: 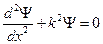 . Решением данного уравнения является функция
. Решением данного уравнения является функция 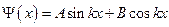 . Используем первое граничное условие:
. Используем первое граничное условие: 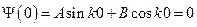 , следовательно,
, следовательно, 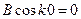 . Но
. Но  , поэтому
, поэтому 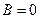 . Применим теперь второе граничное условие:
. Применим теперь второе граничное условие: 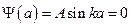 . То есть
. То есть  . Получается, что
. Получается, что  зависит от
зависит от  . Тогда
. Тогда  . Очевидно, что
. Очевидно, что 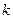 принимает дискретные значения. Вспоминая, что
принимает дискретные значения. Вспоминая, что 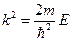 , получим с учётом последнего выражения:
, получим с учётом последнего выражения: 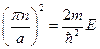 . Отсюда
. Отсюда 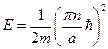 , причём минимальная энергия равна:
, причём минимальная энергия равна: 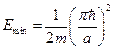 . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид:
. Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид: 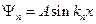 .
.  Волновая функция основного состояния
Волновая функция основного состояния 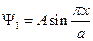 . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу
. Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу 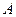 из условия нормировки: вероятность нахождения частицы внутри ямы равна 1:
из условия нормировки: вероятность нахождения частицы внутри ямы равна 1: 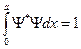 .
. 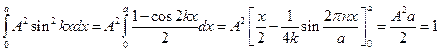 . Отсюда
. Отсюда 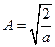 и для волновой функции имеем:
и для волновой функции имеем: 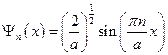 . В случае конечных значений потенциальной энергии существует ненулевая вероятность прохождения частицы за пределы ямы. Мы докажем этот факт чуть позже.
. В случае конечных значений потенциальной энергии существует ненулевая вероятность прохождения частицы за пределы ямы. Мы докажем этот факт чуть позже.
Рассмотрим случай несимметричной ямы: один барьер бесконечный, а другой имеет конечные размеры. Рассмотрим движение в двух областях: 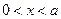 и
и  .
.
1. В первой области уравнение Шредингера имеет вид  . Вводя обозначение
. Вводя обозначение  , получим:
, получим:  . Решение этого уравнения аналогично предыдущему пункту:
. Решение этого уравнения аналогично предыдущему пункту: 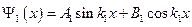 . Из граничных условий, которые соответствуют (1), получаем, что
. Из граничных условий, которые соответствуют (1), получаем, что  и
и 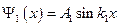 .
.
2. Во второй области уравнение Шредингера имеет вид: 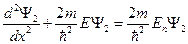 или
или 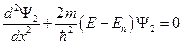 . Введём здесь обозначение:
. Введём здесь обозначение:  . С учётом обозначения можно записать:
. С учётом обозначения можно записать: 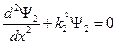 . Решение данного уравнения зависит от
. Решение данного уравнения зависит от 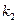 . Имеют место два случая:
. Имеют место два случая: 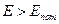 и
и 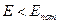 в зависимости от знака
в зависимости от знака 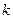 . Разберём каждый случай.
. Разберём каждый случай.
1. Случай 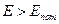 . Общий вид решения исходного уравнения задаётся формулой:
. Общий вид решения исходного уравнения задаётся формулой:  . Волновая функция частоты должна быть непрерывна. Этот факт математически выражается так:
. Волновая функция частоты должна быть непрерывна. Этот факт математически выражается так:  и
и  (2). Подставляя значения функций, получим:
(2). Подставляя значения функций, получим: 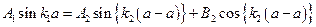 или
или 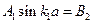 . Считая производные и удовлетворяя равенству (2), получим:
. Считая производные и удовлетворяя равенству (2), получим: 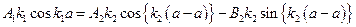 или
или 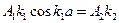 . Мы получили систему уравнений:
. Мы получили систему уравнений: 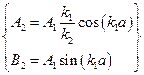 . Эти условия всегда могут быть удовлетворены. Поэтому в случае
. Эти условия всегда могут быть удовлетворены. Поэтому в случае 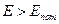 спектр энергии непрерывен, частица при своём движении не локализована в конечной области пространства, её движение инфинитно.
спектр энергии непрерывен, частица при своём движении не локализована в конечной области пространства, её движение инфинитно.
2. Случай 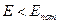 . В этом случае
. В этом случае 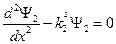 . Решением этого уравнения будет функция следующего вида:
. Решением этого уравнения будет функция следующего вида: 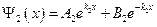 . Первое слагаемое в данном уравнении не имеет физического смысла, иначе волновая функция неограниченно возрастать с увеличением
. Первое слагаемое в данном уравнении не имеет физического смысла, иначе волновая функция неограниченно возрастать с увеличением 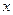 . Поэтому мы обязаны положить
. Поэтому мы обязаны положить 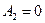 . Получится уравнение:
. Получится уравнение: 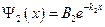 . Эта функция ограничена для любого значения энергии. Однако даже если энергия частицы меньше энергии потенциального барьера, то всё равно существует вероятность обнаружить частицу за барьером. С ростом
. Эта функция ограничена для любого значения энергии. Однако даже если энергия частицы меньше энергии потенциального барьера, то всё равно существует вероятность обнаружить частицу за барьером. С ростом 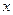 волновая функция убывает.
волновая функция убывает.
Попробуем теперь найти возможные значения энергии, которые будут принимать частица в том случае, если её энергия будет меньше энергии потенциального барьера: 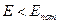 . Рассмотрим уравнения волновых функций в двух различных областях:
. Рассмотрим уравнения волновых функций в двух различных областях: 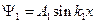 ,
, 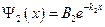 . Из соображений конечности волновой функции и её непрерывности мы можем записать:
. Из соображений конечности волновой функции и её непрерывности мы можем записать:  и
и  . Подставляя конкретный вид соответствующей функции, получим:
. Подставляя конкретный вид соответствующей функции, получим:  и
и 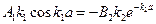 . Разделим второе уравнение на первое. В результате получим:
. Разделим второе уравнение на первое. В результате получим: 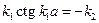 ,
, 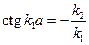 (3). Найдём возможные значения
(3). Найдём возможные значения  и
и 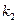 , чтобы найти возможные значения энергии. Известно, что
, чтобы найти возможные значения энергии. Известно, что 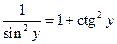 , а
, а 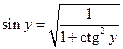 . Возвращаясь к выражениям (3) и используя только что приведённые, получим:
. Возвращаясь к выражениям (3) и используя только что приведённые, получим: 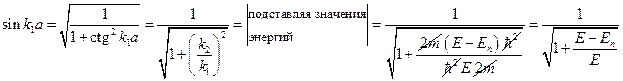 . Подставляя выражение для
. Подставляя выражение для  в предыдущую формулу, получим
в предыдущую формулу, получим  ,
, 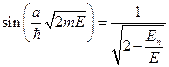 , так как
, так как 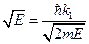 . Тогда
. Тогда  , где
, где 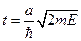 . Решаем последнее уравнение графически. Точки пересечения дают значения энергии. Так как прямая неограничено
. Решаем последнее уравнение графически. Точки пересечения дают значения энергии. Так как прямая неограничено  возрастает, а синус – функция ограниченная, то число точек пересечения будет конечно. Таким образом, и спектр энергии будет дискретным. Итак, мы получили различные выражения для различных видов ям и энергий частицы. Если яма имеет бесконечную глубину, то энергия будет принимать дискретные значения, причём набор этих значений будет бесконечен. Если яма имеет конечную глубину, то в зависимости от энергии частицы будет образовывать либо непрерывный спектр в случае
возрастает, а синус – функция ограниченная, то число точек пересечения будет конечно. Таким образом, и спектр энергии будет дискретным. Итак, мы получили различные выражения для различных видов ям и энергий частицы. Если яма имеет бесконечную глубину, то энергия будет принимать дискретные значения, причём набор этих значений будет бесконечен. Если яма имеет конечную глубину, то в зависимости от энергии частицы будет образовывать либо непрерывный спектр в случае 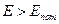 , либо дискретный в случае
, либо дискретный в случае 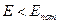 .
.
§ 4.3. Прохождение частицы через потенциальный барьер.
Выше уже было показано, что даже если энергия частицы меньше энергии потенциального барьера, то всё равно существует не нулевая вероятность обнаружить частицу по другую его сторону. Рассмотрим этот случай немного более подробно.
 Область пространства, в которой потенциальная энергия больше, чем в окружающем пространстве называется потенциальным барьером. В случае, представленном на рисунке, энергия потенциального барьера определяется таким образом:
Область пространства, в которой потенциальная энергия больше, чем в окружающем пространстве называется потенциальным барьером. В случае, представленном на рисунке, энергия потенциального барьера определяется таким образом: 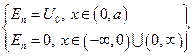 . Будем рассматривать одномерный случай. В случае многомерной потенциальной ямы уравнение Шредингера придётся записывать просто для каждой координаты. Таким образом, не ограничивая общности, мы можем рассматривать одномерный случай. Если частица, имеющая энергию
. Будем рассматривать одномерный случай. В случае многомерной потенциальной ямы уравнение Шредингера придётся записывать просто для каждой координаты. Таким образом, не ограничивая общности, мы можем рассматривать одномерный случай. Если частица, имеющая энергию  , движется в области I, в направлении оси
, движется в области I, в направлении оси 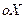 , то в классической механике, если
, то в классической механике, если  , то частица не сможет преодолеть потенциальный барьер, отразится и изменит направление своего движения на противоположное. В квантовой механике вероятность прохода частицы существует. Явление прохода частицы во вторую и третью зоны называется туннельным эффектом. Туннельный эффект характеризуется коэффициентом пропускания барьера:
, то частица не сможет преодолеть потенциальный барьер, отразится и изменит направление своего движения на противоположное. В квантовой механике вероятность прохода частицы существует. Явление прохода частицы во вторую и третью зоны называется туннельным эффектом. Туннельный эффект характеризуется коэффициентом пропускания барьера: 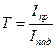 и коэффициентом отражения
и коэффициентом отражения  . Так как частицы не могут оседать на стенках ямы, то
. Так как частицы не могут оседать на стенках ямы, то 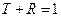 . Найдём эти коэффициенты. Рассмотрим уравнения Шредингера, описывающие состояние частицы в первой, второй и третьей областях.
. Найдём эти коэффициенты. Рассмотрим уравнения Шредингера, описывающие состояние частицы в первой, второй и третьей областях.
1.  , где
, где  .
.
2. 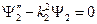 , где
, где 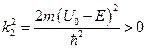 .
.
3. 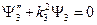 , где
, где 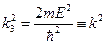 .
.
Решения этих уравнений имеют соответственно вид1:
1. Так как существует вероятность того, что частица будет двигаться как по направлению оси 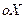 , так и против, то решение будет содержать два слагаемых, описывающих движение частицы, происходящее сонаправлено с осью
, так и против, то решение будет содержать два слагаемых, описывающих движение частицы, происходящее сонаправлено с осью 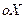 и в противоположную сторону:
и в противоположную сторону:  .
.
2. 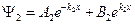 .
.
3. В данном случае движение начинается с точки 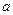 и происходит сонаправлено с осью
и происходит сонаправлено с осью 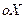 . Поэтому решение уравнения примет вид:
. Поэтому решение уравнения примет вид: 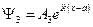 .
.
Получим теперь квантово-механическое выражение для интенсивности. По определению интенсивности можно записать:  . Представим
. Представим  через объём и длину области:
через объём и длину области: 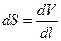 . Тогда
. Тогда  . Здесь
. Здесь 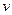 – скорость движения частицы в данном направлении. Очевидно, что число частиц в данной области пространства пропорционально плотности вероятности нахождения частицы в данный момент времени в данной точке пространства:
– скорость движения частицы в данном направлении. Очевидно, что число частиц в данной области пространства пропорционально плотности вероятности нахождения частицы в данный момент времени в данной точке пространства: 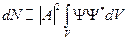 . Данный интеграл даёт значение близкое к единице. Поэтому,
. Данный интеграл даёт значение близкое к единице. Поэтому, 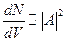 . Подставляя последнее выражение в формулу для импульса, получим:
. Подставляя последнее выражение в формулу для импульса, получим: 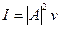 . Распишем скорость частицы через её импульс:
. Распишем скорость частицы через её импульс: 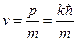 , где
, где 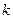 – волновое число. Тогда
– волновое число. Тогда 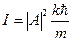 . В последних четырёх формулах под
. В последних четырёх формулах под 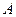 подразумевается один из пяти коэффициентов, стоящих перед экспонентами в решениях уравнения Шредингера. Тогда для интенсивности падающих частиц имеем:
подразумевается один из пяти коэффициентов, стоящих перед экспонентами в решениях уравнения Шредингера. Тогда для интенсивности падающих частиц имеем: 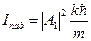 , для интенсивности прошедших –
, для интенсивности прошедших – 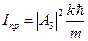 и для интенсивности отражённых –
и для интенсивности отражённых – 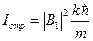 . Таким образом, используя данные выше определения коэффициентов пропускания и отражения для барьера, можно записать:
. Таким образом, используя данные выше определения коэффициентов пропускания и отражения для барьера, можно записать: 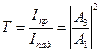 и
и 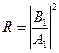 . Получим теперь соотношения между коэффициентами в решении уравнения Шредингера:
. Получим теперь соотношения между коэффициентами в решении уравнения Шредингера: 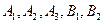 . Будем исходить из того, что волновая функция – непрерывная и гладкая функция. Поэтому выполнены следующие 4 условия:
. Будем исходить из того, что волновая функция – непрерывная и гладкая функция. Поэтому выполнены следующие 4 условия: 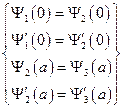 . Подставляя значения функций и их первых производных в заданных точках, получим следующую систему:
. Подставляя значения функций и их первых производных в заданных точках, получим следующую систему: 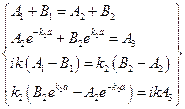 . Решая её, получим:
. Решая её, получим: 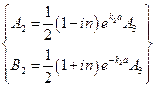 , где
, где 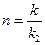 . Сравнивая полученные выражения, можно заметить, что так как
. Сравнивая полученные выражения, можно заметить, что так как 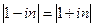 , то
, то 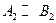 , поэтому мы можем положить
, поэтому мы можем положить 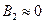 . Исходя из этого допущения, остальные соотношения запишутся довольно легко:
. Исходя из этого допущения, остальные соотношения запишутся довольно легко: 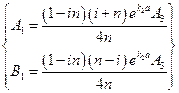 . Таким образом, для
. Таким образом, для 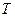 имеем:
имеем:  . Подставляя в полученное ранее соотношение для
. Подставляя в полученное ранее соотношение для 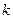 , приведём это уравнение к следующему виду:
, приведём это уравнение к следующему виду:  , или
, или 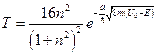 .
. 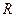 же легко определить из соотношения
же легко определить из соотношения 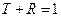 :
: 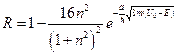 , или
, или 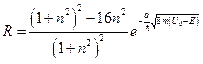 . Если коэффициент пропускания не слишком мал, то есть
. Если коэффициент пропускания не слишком мал, то есть  , мы можем оценить ширину барьера, при которой сквозь него будут проникать частицы:
, мы можем оценить ширину барьера, при которой сквозь него будут проникать частицы: 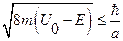 ,
, 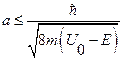 . Подставляя численные значения, получим
. Подставляя численные значения, получим 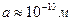 .
.
Распространим теперь наши рассуждения на барьер произвольной формы. В этом случае барьер аппроксимируется малыми прямоугольными барьерами шириной  . Выражение для
. Выражение для  в этом случае будет иметь вид:
в этом случае будет иметь вид: 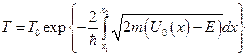 .
.


 Возможность прохождения частицы через потенциальный барьер объясняет холодную эмиссию электронов из металла. Для удаления электронов из металла необходимо затратить некоторую определённую работу. Потенциальная энергия электронов вне металла больше, чем потенциальная энергия внутри металла, причём на границе раздела металл – вакуум потенциальная энергия резко возрастает. Внутри металла в устойчивом состоянии электроны занимают уровни с минимальной энергией. Если вблизи металла имеется электростатическое поле, которое стремится вырвать электроны из метала, то электроны будут стремиться покинут металл. Это явление называется холодной эмиссией электронов. В рамках классической механики объяснить его невозможно, так как поле в металл не проникает, то изменение потенциальной энергии возможно лишь вне металла, а чтобы покинуть металл электроны должны преодолеть потенциальный барьер, но их энергия меньше высоты барьера, поэтому частицы за него проникнуть не могут. Считалось, что электрическое поле понизит высоту потенциального барьера и электроны смогут выходить из металла. Но тогда тока эмиссионных электронов будет достаточно большой, а экспериментально это не наблюдалось. Таким образом, это явление объясняется туннельным эффектом. Тогда коэффициент пропускания такого барьера будет пропорционален
Возможность прохождения частицы через потенциальный барьер объясняет холодную эмиссию электронов из металла. Для удаления электронов из металла необходимо затратить некоторую определённую работу. Потенциальная энергия электронов вне металла больше, чем потенциальная энергия внутри металла, причём на границе раздела металл – вакуум потенциальная энергия резко возрастает. Внутри металла в устойчивом состоянии электроны занимают уровни с минимальной энергией. Если вблизи металла имеется электростатическое поле, которое стремится вырвать электроны из метала, то электроны будут стремиться покинут металл. Это явление называется холодной эмиссией электронов. В рамках классической механики объяснить его невозможно, так как поле в металл не проникает, то изменение потенциальной энергии возможно лишь вне металла, а чтобы покинуть металл электроны должны преодолеть потенциальный барьер, но их энергия меньше высоты барьера, поэтому частицы за него проникнуть не могут. Считалось, что электрическое поле понизит высоту потенциального барьера и электроны смогут выходить из металла. Но тогда тока эмиссионных электронов будет достаточно большой, а экспериментально это не наблюдалось. Таким образом, это явление объясняется туннельным эффектом. Тогда коэффициент пропускания такого барьера будет пропорционален 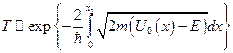 , где
, где 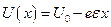 . Здесь
. Здесь 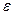 – напряжённость внешнего электрического поля. Очевидно, что плотность тока должна быть пропорциональна коэффициенту пропускания барьера:
– напряжённость внешнего электрического поля. Очевидно, что плотность тока должна быть пропорциональна коэффициенту пропускания барьера: 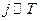 . Таким образом, плотность определяется по экспоненциальному закону:
. Таким образом, плотность определяется по экспоненциальному закону: 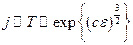 . Когда мерили зависимость
. Когда мерили зависимость 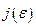 , получилось хорошее согласие с теорией.
, получилось хорошее согласие с теорией.
Ещё одно явление, механизм которого стал понятен благодаря туннельному эффекту – это 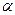 – распад. Так называется самопроизвольное (с точки зрения наблюдателя) вырывание
– распад. Так называется самопроизвольное (с точки зрения наблюдателя) вырывание 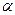 – частиц из ядра. Существует уравнение
– частиц из ядра. Существует уравнение 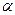 – распада:
– распада: 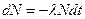 , где
, где 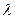 – некоторый коэффициент, а
– некоторый коэффициент, а 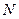 – полное число частиц. Коэффициент
– полное число частиц. Коэффициент 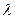 принимает для различных веществ довольно широкий круг значений. Рассмотрим расстановку сил внутри атома. Известно из опыта, что при
принимает для различных веществ довольно широкий круг значений. Рассмотрим расстановку сил внутри атома. Известно из опыта, что при 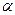 – распаде энергия вылетевших
– распаде энергия вылетевших 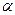 – частиц довольно мала. В то же время, внутри атома между протонами должна действовать колоссальная сила Кулона, которая стремится разорвать атом. Тем не менее, атом сохраняет свою целостность благодаря силам, которые получили название ядерных. Эти силы весьма короткодействующие, но на межнуклонном расстоянии их оказывается достаточно, чтобы «побороть» силы Кулона. Поэтому потенциальная энергия взаимодействия частиц в ядре будет отрицательной. В тоже время, при незначительном удалении от центра атома, в ход вступает сила Кулона. Её действие на таких расстояниях полностью нейтрализует действие ядерных сил. Поэтому потенциальная энергия взаимодействия
– частиц довольно мала. В то же время, внутри атома между протонами должна действовать колоссальная сила Кулона, которая стремится разорвать атом. Тем не менее, атом сохраняет свою целостность благодаря силам, которые получили название ядерных. Эти силы весьма короткодействующие, но на межнуклонном расстоянии их оказывается достаточно, чтобы «побороть» силы Кулона. Поэтому потенциальная энергия взаимодействия частиц в ядре будет отрицательной. В тоже время, при незначительном удалении от центра атома, в ход вступает сила Кулона. Её действие на таких расстояниях полностью нейтрализует действие ядерных сил. Поэтому потенциальная энергия взаимодействия 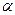 – частиц будет положительной. Таким образом, имеет место быть некоторая потенциальная яма (см. рис. 45). Здесь даны следующие приближения: стенки потенциальной ямы имеют строго вертикальный вид. На самом же деле края ямы несколько более пологи, но в нашем рассмотрении это не играет никакой роли. В классическом рассмотрении
– частиц будет положительной. Таким образом, имеет место быть некоторая потенциальная яма (см. рис. 45). Здесь даны следующие приближения: стенки потенциальной ямы имеют строго вертикальный вид. На самом же деле края ямы несколько более пологи, но в нашем рассмотрении это не играет никакой роли. В классическом рассмотрении 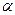 – частица не может преодолеть потенциальный барьер, так как обладает небольшой энергией. Если же считать, сто основную роль в
– частица не может преодолеть потенциальный барьер, так как обладает небольшой энергией. Если же считать, сто основную роль в 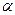 – распаде играют силы Кулона, то энергия вылетевших
– распаде играют силы Кулона, то энергия вылетевших 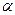 – частиц должна быть довольно высокой. На опыте же такой факт не имел места. Квантовая же механика определяет вероятность прохождения частицей потенциального барьера как не нулевую. То есть, частица преодолеет потенциальный барьер, даже обладая небольшой энергией. На опыте как раз и наблюдались
– частиц должна быть довольно высокой. На опыте же такой факт не имел места. Квантовая же механика определяет вероятность прохождения частицей потенциального барьера как не нулевую. То есть, частица преодолеет потенциальный барьер, даже обладая небольшой энергией. На опыте как раз и наблюдались 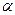 – частицы с небольшими энергиями.
– частицы с небольшими энергиями.
§ 4.4. Линейный гармонический осциллятор.
Частица, совершающая гармонические колебания, называется гармоническим осциллятором. В принципе, если амплитуда колебаний мала, их можно рассматривать как гармонические. Гармонические колебания, рассматриваемые в атомной физике – это колебания атомов в узлах кристаллической решётки, колебания атомов в молекуле и т. д. Как же зависит энергия линейного гармонического осциллятора от энергетического состояния атома, то есть от его главного квантового числа? Для того, чтобы ответить на этот вопрос, необходимо найти собственные значения оператора Гамильтона. Для линейного гармонического осциллятора он имеет вид: 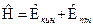 . Распишем теперь каждое слагаемое:
. Распишем теперь каждое слагаемое: 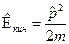 ,
, 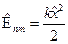 ,
, 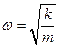 ;
; 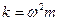 . Тогда оператор Гамильтона примет вид:
. Тогда оператор Гамильтона примет вид: 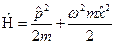 . Чтобы найти собственные значения оператора Гамильтона, подставим ей в уравнение Шредингера:
. Чтобы найти собственные значения оператора Гамильтона, подставим ей в уравнение Шредингера: 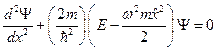 . Осуществим замену переменных:
. Осуществим замену переменных:  ,
, 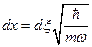 ,
, 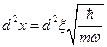 . После подстановки новых переменных, получим:
. После подстановки новых переменных, получим: 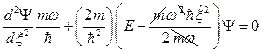 ;
; 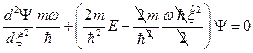 .
. 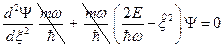 . Введём обозначение:
. Введём обозначение: 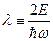 . Тогда уравнение Шредингера примет вид:
. Тогда уравнение Шредингера примет вид: 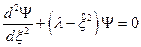 (1). Решим это уравнение. Получим выражение для
(1). Решим это уравнение. Получим выражение для 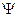 при
при  . В данном случае можно пренебречь во втором слагаемом первым слагаемым. В итоге получится уравнение:
. В данном случае можно пренебречь во втором слагаемом первым слагаемым. В итоге получится уравнение: 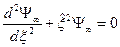 . Решение данного уравнения таково:
. Решение данного уравнения таково: 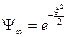 . Волновую функцию
. Волновую функцию 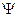 на всей области определения
на всей области определения 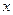 будем искать в виде:
будем искать в виде: 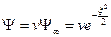 , где
, где 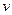 – некоторая функция. Чтобы
– некоторая функция. Чтобы 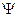 было конечным,
было конечным, 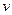 не должно расти быстрее, чем
не должно расти быстрее, чем 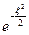 . Подставляя данный вид решения в уравнение (1), получим:
. Подставляя данный вид решения в уравнение (1), получим: 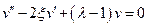 . Будем искать функцию
. Будем искать функцию  в виде полинома:
в виде полинома:  . Подставляем полином в уравнение для
. Подставляем полином в уравнение для  :
:  ,
, 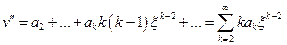 .Таким образом,
.Таким образом, 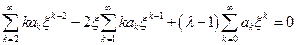 . Данный многочлен будет равен нулю только в том случае, если коэффициенты при одинаковых степенях
. Данный многочлен будет равен нулю только в том случае, если коэффициенты при одинаковых степенях 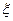 равны нулю:
равны нулю:  . Из этой формулы получается рекуррентное соотношение для коэффициентов
. Из этой формулы получается рекуррентное соотношение для коэффициентов 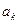 :
: 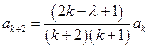 (2). Рассмотрим, к чему стремиться отношение
(2). Рассмотрим, к чему стремиться отношение 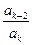 при
при 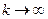 :
: 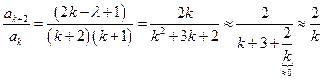 . Это значит, что при
. Это значит, что при 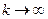
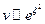 . Действительно, разложим экспоненту в ряд Тейлора и посмотрим на поведение коэффициентов ряда при больших
. Действительно, разложим экспоненту в ряд Тейлора и посмотрим на поведение коэффициентов ряда при больших 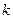 .
.  ; таким образом,
; таким образом, 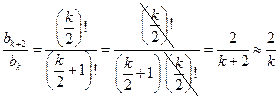 . Итак,
. Итак, 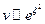 . Оборвём теперь ряд на члене с номером
. Оборвём теперь ряд на члене с номером 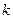 и переобозначим
и переобозначим 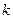 в
в 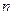 . Мы можем сделать так, если
. Мы можем сделать так, если 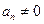 , а
, а 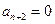 . Это достигается в том случае, когда
. Это достигается в том случае, когда 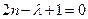 (следует из рекуррентного соотношения),
(следует из рекуррентного соотношения),  . Возвращаясь к значению
. Возвращаясь к значению 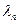 , получим:
, получим:  . Отсюда
. Отсюда 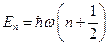 . Минимальная энергия, которой может обладать квантовая частица, как следует из этого соотношения, будет
. Минимальная энергия, которой может обладать квантовая частица, как следует из этого соотношения, будет  . Эта энергия называется энергией вакуума. Таким образом, квантовомеханическая частица не может находиться в состоянии покоя. Иначе это противоречило бы соотношению неопределённостей. Наличие этой минимальной энергии доказывается экспериментально. Доказательство существования минимальной энергии было проведено в экспериментах по рассеянию света кристаллами. Если с уменьшением температуры амплитуда колебания атома уменьшается и стремиться к нулю, то в соответствии с законами классической механики, начиная с некоторой температуры, рассеяние света должно вообще прекращаться. В квантовой механике амплитуда колебаний атома должна стремиться не к нулю, а к некоторому предельному значению, обусловленному наличию нулевой энергии. Поэтому при понижении температуры, интенсивность рассеяния будет стремиться к некоторому пределу, что и наблюдалось в опыте.
. Эта энергия называется энергией вакуума. Таким образом, квантовомеханическая частица не может находиться в состоянии покоя. Иначе это противоречило бы соотношению неопределённостей. Наличие этой минимальной энергии доказывается экспериментально. Доказательство существования минимальной энергии было проведено в экспериментах по рассеянию света кристаллами. Если с уменьшением температуры амплитуда колебания атома уменьшается и стремиться к нулю, то в соответствии с законами классической механики, начиная с некоторой температуры, рассеяние света должно вообще прекращаться. В квантовой механике амплитуда колебаний атома должна стремиться не к нулю, а к некоторому предельному значению, обусловленному наличию нулевой энергии. Поэтому при понижении температуры, интенсивность рассеяния будет стремиться к некоторому пределу, что и наблюдалось в опыте.
Найдём теперь собственные функции. Из выражения (2) следует, что чётность функции 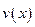 совпадает с
совпадает с 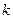 . Таким образом,
. Таким образом, 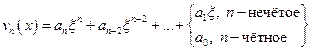 ,
,  . Положим, что
. Положим, что 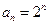 . Тогда остальные коэффициенты определим через рекуррентное соотношение:
. Тогда остальные коэффициенты определим через рекуррентное соотношение: 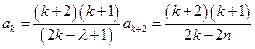 , с учётом выражения
, с учётом выражения 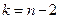 , получим:
, получим: 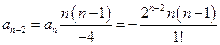 . Аналогично,
. Аналогично, 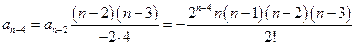 . Полином, в котором
. Полином, в котором 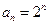 , а
, а  , называется полиномом Эрмита:
, называется полиномом Эрмита: 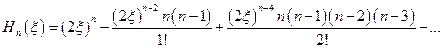 . Из свойств полинома Эрмита следует, что
. Из свойств полинома Эрмита следует, что 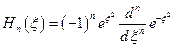 . Тогда волновая функция
. Тогда волновая функция  , принадлежащая собственному значению
, принадлежащая собственному значению 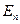 может быть представлена в виде:
может быть представлена в виде: 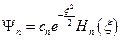 , где
, где 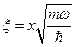 . Коэффициент
. Коэффициент 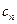 находится из условия нормировки:
находится из условия нормировки: 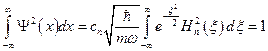 . Отсюда
. Отсюда  . Тогда волновая функция окончательно примет вид:
. Тогда волновая функция окончательно примет вид:  . Итак, мы получили выражения для собственных функций оператора Гамильтона.
. Итак, мы получили выражения для собственных функций оператора Гамильтона.
§ 4.5. Движение в поле центральных сил.
Рассмотрим движение электрона в центрально-симметричном кулоновском поле ядра. Уравнение Шредингера для частицы в центрально-симметричном поле имеет вид:  . Будем рассматривать для удобства движение частицы в сферической системе координат. Лапласиан в такой системе координат имеет вид:
. Будем рассматривать для удобства движение частицы в сферической системе координат. Лапласиан в такой системе координат имеет вид: 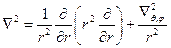 (1), где
(1), где 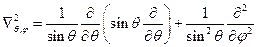 (1). Решение уравнения Шредингера будем искать в виде:
(1). Решение уравнения Шредингера будем искать в виде:  . Подставляя решение в уравнение Шредингера, получим:
. Подставляя решение в уравнение Шредингера, получим: 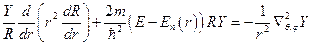 . Разделяя переменные, можно записать:
. Разделяя переменные, можно записать: 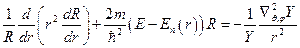 . Так как обе части этого уравнения входят независимые переменные и эти части равны, то мы должны положить
. Так как обе части этого уравнения входят независимые переменные и эти части равны, то мы должны положить 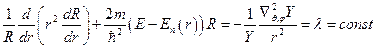 . Таким образом, это уравнение распадается на два:
. Таким образом, это уравнение распадается на два: 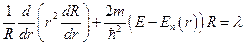 (2) и
(2) и 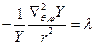 (3). Решение уравнения (2) зависит от самого поля. Эта зависимость обуславливается наличием в уравнении
(3). Решение уравнения (2) зависит от самого поля. Эта зависимость обуславливается наличием в уравнении  . Рассмотрим поэтому сначала решение уравнения (3). Распишем лапласиан, связанный с поворотом тела в пространстве:
. Рассмотрим поэтому сначала решение уравнения (3). Распишем лапласиан, связанный с поворотом тела в пространстве: 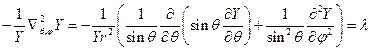 . Производя некоторые простейшие преобразования, получим:
. Производя некоторые простейшие преобразования, получим: 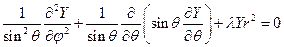 . Так как
. Так как 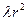 не зависит ни от
не зависит ни от 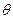 , ни от
, ни от 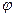 , то мы можем ввести некоторое переобозначение и рассматривать в дальнейшем это произведение как константу:
, то мы можем ввести некоторое переобозначение и рассматривать в дальнейшем это произведение как константу: 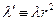 . Тогда
. Тогда 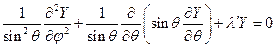 . Это уравнение допускает разделение переменных. Будем искать его решение в виде:
. Это уравнение допускает разделение переменных. Будем искать его решение в виде: 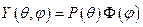 . Подставляя его в последнее уравнение, получим:
. Подставляя его в последнее уравнение, получим:  . Разделим на
. Разделим на 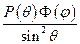 :
: 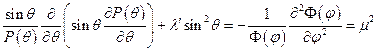 , где
, где 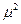 – константа разделения. Разобьём это уравнение на две части:
– константа разделения. Разобьём это уравнение на две части: 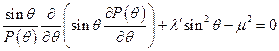 и
и 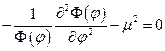 ,
, 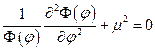 . Запишем систему
. Запишем систему  . Решение первого уравнения данной системы имеет вид:
. Решение первого уравнения данной системы имеет вид: 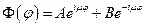 . Из требования однозначности решения следует, что
. Из требования однозначности решения следует, что 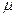 должно быть любым положительным или отрицательным числом. Поэтому все собственные функции дифференциального уравнения (4) могут быть представлены формулой:
должно быть любым положительным или отрицательным числом. Поэтому все собственные функции дифференциального уравнения (4) могут быть представлены формулой: 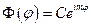 , где
, где 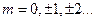 . Постоянная
. Постоянная 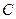 находится из условия нормировки и равна
находится из условия нормировки и равна 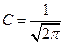 . Таким образом,
. Таким образом, 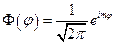 . Решая уравнение (5), перейдём к новым координатам:
. Решая уравнение (5), перейдём к новым координатам: 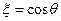 . Тогда
. Тогда 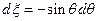 и
и  ;
; 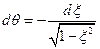 . С учётом последних преобразований перепишем уравнение (5):
. С учётом последних преобразований перепишем уравнение (5): 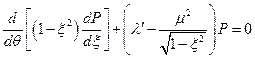 . Чтобы привести данное уравнение к стандартному виду введём обозначение:
. Чтобы привести данное уравнение к стандартному виду введём обозначение: 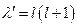 , где
, где  – неотрицательное целое число. Тогда решением данного уравнения будет присоединённый полином Лежандра:
– неотрицательное целое число. Тогда решением данного уравнения будет присоединённый полином Лежандра: 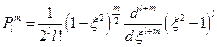 . Причём, при заданном
. Причём, при заданном  ,
, 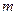 может принимать только
может принимать только 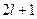 значение:
значение:  . Волновая функция должна удовлетворять условию нормировки:
. Волновая функция должна удовлетворять условию нормировки: 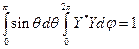 ;
; 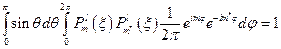 . Так как
. Так как 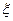 и
и 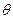 связаны однозначно, то мы можем переписать последний интеграл в виде:
связаны однозначно, то мы можем переписать последний интеграл в виде:  . Выражение, стоящее под внутренним интегралом, не зависит от
. Выражение, стоящее под внутренним интегралом, не зависит от 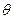 , поэтому мы можем вычислять каждый интеграл по отдельности и полученные значения перемножить. Известно, что
, поэтому мы можем вычислять каждый интеграл по отдельности и полученные значения перемножить. Известно, что 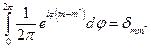 , где
, где  – символ Кронекера. Второй интеграл даёт значение
– символ Кронекера. Второй интеграл даёт значение 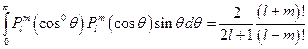 . Собственная функция уравнения (5) запишется в виде:
. Собственная функция уравнения (5) запишется в виде: 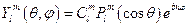 . Тогда с помощью условия нормировки, мы можем записать:
. Тогда с помощью условия нормировки, мы можем записать: 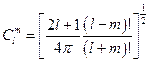 . Подставляя данное значение в последнюю формулу, получим:
. Подставляя данное значение в последнюю формулу, получим: 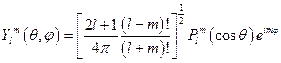 . Мы получили угловую функцию, описывающую движение частиц в центрально – симметричном поле.
. Мы получили угловую функцию, описывающую движение частиц в центрально – симметричном поле.
Для получения энергий стационарных состояний необходимо знать момент импульса системы. Это есть прямое следствие правил квантования. Рассмотрим моменты импульса частицы при движении в поле центральных сил: 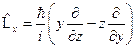 ;
; 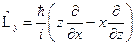 ;
;  . Имеют место следующие правила коммутации:
. Имеют место следующие правила коммутации: 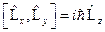 ,
, 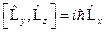 ,
,  . Таким образом, нельзя одновременно указать два различных значения момента импульса. Однако можно показать, что
. Таким образом, нельзя одновременно указать два различных значения момента импульса. Однако можно показать, что  . Это значит, что любая из проекций момента импульса и квадрат момента импульса могут иметь одновременно определённые значения. Так как рассматриваемое поле сферически симметрично, перейдём к сферической системе координат:
. Это значит, что любая из проекций момента импульса и квадрат момента импульса могут иметь одновременно определённые значения. Так как рассматриваемое поле сферически симметрично, перейдём к сферической системе координат:  . Тогда,
. Тогда, 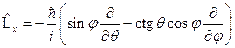 ;
; 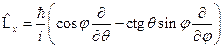 ;
; 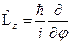 , а
, а  . Найдём собственные значения операторов
. Найдём собственные значения операторов 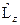 и
и 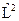 . Для этого подействуем ими на функции
. Для этого подействуем ими на функции 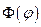 и
и  соответственно:
соответственно: 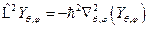 или, с помощью уравнения (3),
или, с помощью уравнения (3), 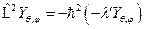 . Собственной функцией оператора
. Собственной функцией оператора 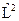 является функция
является функция  , то есть угловая часть волновой функции , а его собственным значением –
, то есть угловая часть волновой функции , а его собственным значением – 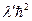 . Вспоминая наше обозначение для
. Вспоминая наше обозначение для 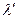 :
: 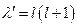 . Тогда,
. Тогда, 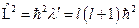 . Таким образом, мы нашли собственное значение для оператора
. Таким образом, мы нашли собственное значение для оператора 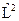 . Посчитаем теперь собственное значение для оператора
. Посчитаем теперь собственное значение для оператора 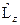 :
: 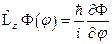 . Подставляя значение функции
. Подставляя значение функции 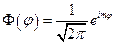 , получим:
, получим: 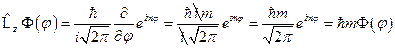 . Таким образом,
. Таким образом, 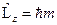 . Так как оператор
. Так как оператор 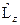 имеет строго определённое значение, то операторы
имеет строго определённое значение, то операторы 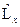 и
и 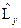 конкретных значений не имеют и иметь не будут. Отметим также, что так как исходные функции, для которых искались собственные значения не зависят от вида центрально – симметричного поля, то и собственные значения и функции для всех таких полей будут одинаковы.
конкретных значений не имеют и иметь не будут. Отметим также, что так как исходные функции, для которых искались собственные значения не зависят от вида центрально – симметричного поля, то и собственные значения и функции для всех таких полей будут одинаковы.
В атомной физике часто говорят, что момент импульса частицы равен 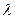 , так как все функции нормируются на
, так как все функции нормируются на 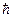 или на
или на 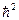 . Значение
. Значение  называют орбитальным квантовым числом, то есть числом, которое характеризует момент импульса электрона. В зависимости от того, какое значение принимает орбитальное квантовое число, состояние движения частицы с различными моментами импульса имеет разные названия.
называют орбитальным квантовым числом, то есть числом, которое характеризует момент импульса электрона. В зависимости от того, какое значение принимает орбитальное квантовое число, состояние движения частицы с различными моментами импульса имеет разные названия.

| ||||||
| Состояние | S | P | D | F | G | H |
Число 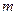 называют магнитным квантовым числом. Им определяется поведение частицы в магнитном поле.
называют магнитным квантовым числом. Им определяется поведение частицы в магнитном поле.
Дата добавления: 2016-01-30; просмотров: 2224;
