SOMETHING ABOUT MATHEMATICAL SENTENCES
You will remember that a mathematical sentence containing an equal sign is an equation. The two parts of an equation are called its members. A mathematical sentence that is either true or false but not both is called a closed sentence. Both true and false sentences are closed. To decide whether a closed sentence containing an equal sign is true or false, we check to see that both elements, or members of the sentence name the same number. To decide whether a closed sentence containing an ≠ sign is true or false, we check to see that both elements do not name the same number.
The relation of equality between two numbers satisfies the following basic axioms for the numbers a, b, and c.
Reflexive: a = a Symmetric: If a = b, then b = a. Transitive: If a = b and b = c then a = c.
In all branches of mathematics you need to write many sentences about numbers. While the symbol = in an arithmetic sentence means is equal to, another symbol, ≠,means is not equal to. When an = sign is replaced by ≠ sign, the opposite meaning is implied. Thus 8 = 11 - 3 is read eight is equal to eleven minus three while 9 + 6 ≠ 13 is read nine plus six is not equal to thirteen.
The important feature about a sentence involving numerals is that it is either true or false, but not both. There is nothing incorrect about writing a false sentence; in fact in some mathematical proofs it is essential that you write a false sentence. Since mathematical language is so direct and concise we must have a good understanding of the meaning of each symbol that we use.
We already know that if we draw one short line across the symbol we shall change it to ≠. The symbol ≠implies either of two things - is greater than or is less than. In other words the sign ≠in 3 + 4 ≠ 6 tells us only that the numerals 3 + 4 and 6 name different numbers, but does not tell us which numeral names the greater or the lesser of the two numbers.
To know which of the two numbers is greater let us use the conventional symbols < and >. < means is less than while > means is greater than. These are inequality symbols or ordering symbols because they indicate order of numbers. 6 < 7 is read six is less than seven. 29 > 3 is read twenty nine is greater than three.
The signs which express equality or inequality (=, ≠, <, >) are called relation symbols because they indicate how two expressions are related.
FRACTIONS
A fraction is a number expressed as the quotient of two mathematical expressions, often integers. Fractions come in the form 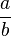 , where a is called the numerator and b is called the denominator.
, where a is called the numerator and b is called the denominator.
Sometimes the word "fraction" means the quotient of two integers. Under this definition,  is a fraction, but
is a fraction, but 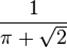 is not.
is not.
If the numerator is larger than the denominator, it is called an improper fraction, and is greater than one. An example of an improper fraction is  , which is 25 wholes and a half;
, which is 25 wholes and a half;  as a mixed number. Also,
as a mixed number. Also,  . For example,
. For example,  would be
would be  .
.
Meanwhile, if the numerator is larger than the denominator, it is called a proper fraction, and is less than one.
Multiplying fractions is very easy:
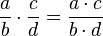 .
.
For nonzero a,  . This gives us a useful identity:
. This gives us a useful identity:
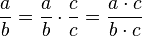
allowing us to "force" values of the numerator or denominator. Some call this multiplying by one creatively.
Adding fractions is somewhat harder. If both the summands have the same denominator, we can use the distributive property:
 .
.
But if they're different, we can multiply by one creatively to force their denominators to line up:
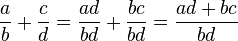 .
.
This formula is not terribly useful to memorize; knowing the technique is much more helpful. If we're working with integers, instead of 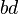 in the denominator, we can use the least common multiple of b and d.
in the denominator, we can use the least common multiple of b and d.
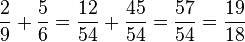
Note that we could have taken a shortcut using the least common multiple:
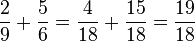
We multiplied the first fraction by 2/2 and the second by 3/3.
You can convert a mixed number (a, surprisingly, mixed fraction — 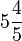 is a mixed number) into an improper fraction (a fraction in which the numerator is larger than the denominator) by doing three things:
is a mixed number) into an improper fraction (a fraction in which the numerator is larger than the denominator) by doing three things:
- Multiply the whole number (the
 ) by the denominator (the other
) by the denominator (the other  ) of the fractional part. In the example above, to change
) of the fractional part. In the example above, to change 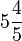 to a mixed number, first multiply
to a mixed number, first multiply 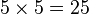 .
. - Add the numerator of the fractional part to that product. In the example,
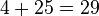 .
. - The resulting sum is the numerator of the new (improper) fraction, with the denominator remaining the same in both the mixed number and the improper fraction. In the example,
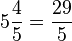 .
.
Likewise, you can convert an improper fraction into a mixed number by following another 3 rules:
- Divide the numerator by the denominator. Let's say, for example,
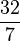 .
. 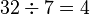 with 4 left over (the remainder)
with 4 left over (the remainder) - The quotient (without the remainder) becomes the whole number part of the mixed number. The remainder becomes the numerator of the fractional part. In the example, 4 is the whole number part and 4 is the numerator of the fractional part.
- The new denominator is the same as the denominator of the improper fraction. In the example, the denominator is 7. Thus
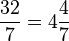 .
.
DECIMAL NUMERALS
In ournumeration system weuse ten numerals called digits. These digits are used over and over again in various combinations. Suppose, you have been given numerals 1, 2, 3 and have been asked to write all possible combinations of these digits.
You may write 123, 132, 213 and so on. The position in which each digit is written affects its value. How many digits are in the numeral 7086? How many place value positions does it have? The diagram below may prove helpful. A comma separates each group of period. To read 529, 248, 650, 396, you must say: five hundred twenty-nine billion, two hundred forty-eight million, six hundred fifty thousand, three hundred ninety-six.
| Billions period | Millions period | Thousands period | Ones period | ||||||||
| Hundredb illions | Ten billions | One billion | Hundred millions | Ten millions | One million | hundred thousands | Ten thousands | One thousand | hundreds | tens | ones |
| 9, | 8, | 0, |
But suppose you have been given a numeral 587,9 where 9 has been separated from 587 by a point, but not by a comma. The numeral 587 names a whole number. The sign (.) is called a decimal point. All digits to the left of the decimal point represent whole numbers. All digits to the right of the decimal point represent fractional parts of 1.
The place-value position at the right of the ones place is called tenths. You obtain a tenth by dividing 1 by 10. Such numerals like 687,9 are called decimals. You read .2 as two tenths. To read .0054 you skip two zeroes and say fifty-four ten thousandths.
Decimals like .666…, or .242424…, are called repeating decimals. In a repeating decimal the same numeral or the same set of numerals is repeated over and over indefinitely.
We can express rational numbers as decimal numerals. See how it may be done. 31 / 100 = 0.31. 4 / 25 = 4 x 4 / 4 x 25 = 16 / 100 = 0.16. The digits to the right of the decimal point name the numerator of the fraction, and the number of such digits indicates the power of 10 which is the denominator.
For example, 217 denotes a numerator 217 and a denominator of ten cubed or 1000. In our development of rational numbers we have named them by fractional numerals.
We know that rational numerals can just as well be named by decimal numerals. As you might expect, calculations with decimal numerals give the same results as calculations with the corresponding fractional numerals.
Before performing addition with fractional numerals, the fractions must have a common denominator. This is also true of decimal numerals. When multiplying with fractions, we find the product of the numerators and the product of denominators. The same procedure is used in multiplication with decimals.
THE GAME OF CHESS
 Youwill probably know that the game of chess so popular nowadays all over the world comes from India. According to an old legend it was invented by king Shirham’s visier Sissa Ben Dahir and presented to the king by the latter. The King was very pleased and asked Sissa Ben whether he could do anything to thank him for the present. His vizier’s desire seemed quite easy to fulfil. He asked his king to give him a grain of wheat to put on the first square of the chessboard, and two grains to put on the second square, and four grains to put on the third square and eight grains to put on the fourth and so on doubling the number for eachs square that came next. He said he wanted the grains to cover all 64 squares of the board.
Youwill probably know that the game of chess so popular nowadays all over the world comes from India. According to an old legend it was invented by king Shirham’s visier Sissa Ben Dahir and presented to the king by the latter. The King was very pleased and asked Sissa Ben whether he could do anything to thank him for the present. His vizier’s desire seemed quite easy to fulfil. He asked his king to give him a grain of wheat to put on the first square of the chessboard, and two grains to put on the second square, and four grains to put on the third square and eight grains to put on the fourth and so on doubling the number for eachs square that came next. He said he wanted the grains to cover all 64 squares of the board.
The king thought his vizier did not ask too much for what he had done and said that he would certainly give him what he asked for:
And he told his men to bring a large bag full of wheat.
But when the counting began, with 1 grain for the first square, 2 for the second, 4 for the third and so on the bag was emptied before the twrentieth square was covered with wheat.
More bags were brought before the king but the number of grains needed increased so rapidly that the king soon saw he would not be able to keep his word
The thing is that a bushel of wheat contains about 5,000,000 grains. The king had, certainly, no idea of it and did not expect that he would have to give 4000 billion bushels to Sissa Ben.
Since the world production of wheat averages about 2,000,000,000 bushels a year, the amount of wheat asked by the vizier equaled the world’s wheat production for the period of some two thousands years.
Thus king Shirham found that he either had to remain constantly in debt to his vizier or cut his head off. He thought it best to choose the latter alternative.
Дата добавления: 2015-12-01; просмотров: 3673;
