Квантовый компьютер

В диапазоне ниже 0,1мкм (100нм) мир становится квантовым, вероятностным и неопределенным (следующий предел 10-1,0 нм соответствует размеру простых биомолекул, 1,0-0,1 нм – размер отдельных атомов и простейших молекул).

Идея квантовых вычислений была впервые высказана советским математиком Ю.И. Маниным в 1980 году. Активное обсуждение этой идеи началось после опубликования в 1982 году статьи американского физика-теоретика, нобелевского лауреата Р.Фейнмана.

За единицу измерения информации в квантовых компьютерах (КК) принят кубит или квантовый бит (qubit, Quantum Bit). Кубитом принято также называть элементарную ячейку квантового компьютера. Кубит в определенный момент времени с некоторой вероятностью равен и 0, и 1 (суперпозиция).

Во время работы КК отдельные кубиты связаны между собой эффектом квантовой запутанности (entanglement). Несколько связанных кубитов с неопределённым значением содержат не одно число, а все возможные числа, умещающиеся в ячейке такой разрядности. Т.е., квантовый компьютер одновременно рассматривает все решения задачи, и правильные, и ошибочные.

Основная проблема – при считывании информации неопределённость исчезает. Из множества содержавшихся решений остаётся только одно, причём не самое верное, а первое попавшееся. Т.е. необходимо решить задачу отсеивания ненужных вариантов. Это делают с помощью квантовых алгоритмов, которые состоят из специальных операций, влияющих на кубиты.

Кубитами, например, могут служить ионы, подвешенные в электромагнитном поле. Для выполнения квантовых операций требуется внешнее воздействие (например, с помощью лазера или микроволн). Любое взаимодействие между кубитами и окружающей средой может привести к декогеренции (нарушения квантовой запутанности), которая делает продолжение работы невозможным. Чтобы избежать помех, квантовые компьютеры часто помещают в вакуум и охлаждают почти до абсолютного нуля.

Примеры применения:

Алгоритм Шора. Предназначен для факторизации чисел (разложения их на простые множители). Для традиционных компьютеров количество шагов, необходимое для факторизации числа известными алгоритмами, экспоненциально растёт с каждым дополнительным разрядом и быстро переходит границы возможного. На этом свойстве держится криптография с открытым ключом. На квантовом компьютере с помощью алгоритма Шора, время вычислений растёт не экспоненциально, а гораздо медленнее. Квантовый компьютер позволяет факторизовать число, состоящее из N разрядов, за N² операций.

Алгоритм Гровера. Позволяет найти нужный элемент в неотсортированном списке из N элементов, выполнив лишь N^1/2 сравнений. На обычном компьютере для решения той же задачи потребовалось бы N сравнений.

Реализация. В D-Wave заявлено о создании, однако, это не КК в классическом понимании. В основе машины D-Wave лежит охлаждённая до -273 градусов по Цельсию микросхема с решёткой, построенной из сверхпроводящих квантовых интерферометров. Именно их в компании называют кубитами. Значение кубитов D-Wave, как и значение кубитов в настоящем квантовом компьютере, может быть неопределённым, однако они не связаны между собой с помощью квантовой запутанности.

Машина D-Wave не годится для алгоритмов, которые используют квантовые вентили. Ни алгоритм Шора, ни алгоритм Гровера на ней не пойдут. Вместо этого она использует для работы совершенно иной принцип – так называемые адиабатические квантовые вычисления. Это значительно ограничивает её возможности, но позволяет не беспокоиться о декогеренции и других проблемах, сопровождающих обычные квантовые вычислители.

Адиабатические квантовые компьютеры представляют собой специализированные устройства, предназначенные для решения единственной задачи: поиска оптимального решения функции, которая определена энергетическим состоянием всех кубитов вместе. Выполнять операции над отдельными кубитами они не способны, но в данном случае этого и не требуется.

Нейрокомпьютер

Создание компьютера на основе нейронных систем живого мира базируется на теории перцептронов (Розенблатт) – искусственных нейронных сетей. ИНС обладают высокой надежностью и могут самообучаться. Используются в задачах распознавания образов, при решении сложных задач параллельной обработки информации.

Нейрокомпьютеры можно строить на базе нейрочипов, которые функционально ориентированы на конкретный алгоритм. Для решения задач разного типа требуется нейронная сеть разной топологии. Возможна эмуляция нейрокомпьютеров (моделирование) – как программно на мощных КС, так и программно-аппаратно на цифровых СБИС.

Основные проблемы:

1. создание искусственных нейронов;

2. реализация пространственной структуры из десятков и сотен триллионов межрайонных связей.

Первая проблема легко решается современными технологиями производства СБИС. Решение второй проблемы для современных микроэлектронных ИНС пока невозможно.

С проблемами и перспективами развития аппаратных средств тесно связаны два закона:

1. Закон Мура;

2. Закон Амдала.

Закон Мура утверждает, что удвоение числа транзисторов в микросхеме происходит каждые полтора-два года. Эту закономерность Гордон Мур (Gordon Moore) обнаружил в 1965 году, представив в виде графика рост производительности запоминающих микросхем. Новые модели микросхем разрабатывались спустя одинаковые периоды – 18-24 месяца после появления их предшественников. Их емкость при этом возрастала примерно вдвое. Некоторые специалисты считают, что действие этого закона продлится до 2015 года.

Закон Амдала утверждает, что для оценки ускорения S, которое может быть получено на вычислительной системе из р процессоров при заданной величине f, следует воспользоваться формулой:

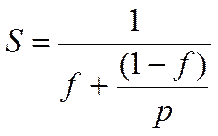
Здесь предполагается, что величина f (где 0 < f < 1) – доля операций, которые должны быть реализованы в процессе выполнения программы последовательно. Крайние значения соответствуют полностью параллельным (f = 0) и полностью последовательным программам (f = 1). Некоторые специалисты образно называют этот закон «страшным», указывая на следующий факт. Предположим, что в программе всего лишь 10% последовательных операций (f = 0.1). Закон утверждает, что, сколько бы процессоров не было использовано, максимальное ускорение работы может быть не более чем в 10 раз. (Причем, 10 получается только в том случае, если время исполнения параллельной части равно нулю).