Развитие представлений о природе света

В конце XVII в. на основе многовекового опыта и развития представлений о свете возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и X. Гюйгенс).

Согласно корпускулярной теории свет представляет собой поток частиц (корпускул), испускаемых светящимися телами и летящих по прямолинейным траекториям. Движение световых корпускул Ньютон подчинил сформулирован­ным им законам механики. Так, отражение света понималось аналогично отражению упругого шарика при ударе о плоскость, где также соблюдается закон равенства углов падения и отражения. По теории Ньютона скорость распространения света в среде должна быть всегда больше скоро­сти его распространения в вакууме.

Согласно волновой теории, развитой на основе аналогии оптических и акустических явлений, свет представляет собой упругую волну, распространяющуюся в особой среде - эфире. Эфир заполняет все мировое пространство, пронизывает все тела и обладает механическими свойствами - упругостью и плотностью.

Волновая теория приводит к выводу, отличному от вывода теории Ньютона. По теории Гюйгенса скорость распространения света в среде должна быть всегда меньше скорости его распространения в вакууме.

Несмотря на признание волновой теории, она обладала целым рядом недостатков. Например, явления интерференции, дифракции и поляризации могли быть объяснены только в том случае, если световые волны считать поперечными. Далее эксперименты показали, что скорость распространения света в разных средах различна, поэтому эфир должен обладать в разных средах различными свойствами. Теория Гюйгенса не могла объяснить также физической природы наличия разных цветов.

Наука о свете накапливала экспериментальные данные, свидетельствующие о взаимосвязи световых, электрических и магнитных явлений, что позволило Максвеллу создать электромагнитную теорию. Согласно электромагнитной теории Максвелла,

с/υ = 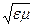= n, (26.1)

где с и υ — соответственно скорости распространения света в вакууме и в среде с диэлектрической проницаемостью ε и магнитной проницаемостью μ. Это соотноше­ние связывает оптические, электрические и магнитные постоянные вещества. По Макс­веллу, ε и μ — величины, не зависящие от длины волны света, поэтому электромагнит­ная теория не могла объяснить явление дисперсии (зависимость показателя преломле­ния от длины волны). Теория Максвелла не смогла объ­яснить процессов испускания и поглощения света, фотоэлектрического эффекта, комптоновского рассеяния и т. д.

Эта трудность была преодолена Лоренцем, предложившим электронную теорию, согласно которой диэлектрическая проницае­мость ε зависит от длины волны падающего света. Теория Лоренца ввела представле­ние об электронах, колеблющихся внутри атома, и позволила объяснить явления испускания и поглощения света веществом. Теории Лоренца, в свою очередь, не смогла объяснить многие явления, связанные с взаимодействием света с веществом, в ча­стности вопрос о распределении энергии по длинам волн при тепловом излучении черного тела.

Перечисленные затруднения и противоречия были преодолены благодаря гипотезе М. Планка, согласно которой излучение и поглощение света происходит не непрерывно, а дискретно, т. е. определенными порциями (квантами), энергия которых определяется частотой ν

Е₀ = hν, (26.2)

где h= 6,625×10^-34 Дж×с - постоянная Планка.

Теория Планка объяснила тепловое излуче­ние черного тела. Эйнштейн создал квантовую теорию света, согласно которой не только излучение света, нo и его распространение происходит в виде потока световых квантов — фотонов, энергия которых определяется соотношением (26.2), а масса и импульс

m_ф = Е₀/с² = hv/с²= h/λс, (26.3)

р= hv/с = h/λ. (26.4)

Квантовые представления о свете хорошо согласуются с законами излучения и поглощения света, законами взаимодействия света с веществом. Явления интерференция, дифракция и поляризация света объясняются на основе волновых представлений. Все многообразие изученных свойств и законов распрост­ранения света, его взаимодействия с веществом показывает, что свет имеет сложную природу. Он представляет собой единство противоположных видов движения — корпускулярного (квантового) и волнового (электромагнитного). Длительный путь развития привел к современным представлениям о двойственной корпускулярно-волновой природе света. Выражения (26.2; 26.3; 26.4) связывают корпускулярные характеристики излучения — массу и энергию кванта — с волновыми — частотой колебаний и длиной волны. Таким образом, свет представляет собой единство дискретности и непрерывности.

26.2. Интерференция света

Интерференцию света можно объяснить, рассматривая интерференцию волн. Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — не­ограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников.

Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления:

ξ₁ = А₁cos(ωt+φ₁) и ξ₂ = А₂cos(ωt+φ₂). (26.5)

Амплитуда резуль­тирующего колебания в данной точке:

А² = А₁²+А₁²+2А₁А₂соs(φ₂ – φ₁).(26.6)

Так как волны когерентны, то cos (φ₂ – φ₁) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (I~A²)

I = I₁ + I₂+2 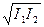cos(φ₂ – φ₁). (26.7)

В точках пространства, где cos (φ₂ – φ₁)>0, интенсивность I > I₁ + I₂,

где сos(φ₂ – φ₁)<0, интенсивность I < I₁ + I₂.

Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других—мини­мумы интенсивности. Это явление называется — интерференцией света.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференци­онная картина.

Пусть разделение на две когерентные волны происходит в определенной точке. Дo точки, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления n₁ прошла путь s₁, вторая — в среде с показателей преломления n₂- путь s₂. Первая волна возбудит колебание х₁= А₁ cosω(t-s₁/υ₁),вторая волна—колебание х₂ =А₂cosω(t-s₂/υ₂), где υ₁=c/n₂, υ₂=c/n₂ — соответственно фазовая скорость первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке, где наблюдается интерференционная картина, равна

δ =ω(s₂/υ₂- s₁/υ₁)= 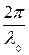(s₂ n₂ – s₁n₁). (26.8)

Произведение геометрической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L = s n,

δ = 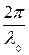(L₂ – L₁), (26.9)

a L₂—L₁ = Δ - разность оптических длин проходимых волнами путей — называется оптической разностью хода.

δ = 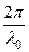Δ. (26.10)

Если оптическая разность хода равна целому числу длин волн в вакууме

Δ = ± mλ₀ ( m= 1,2,3, …), (26.11)

то δ = ±2mπ и колебания, возбуждаемые в точке обеими волнами, будут проис­ходить в одинаковой фазе. Следовательно, (26.11) является условием интерференционного максимума.

Если оптическая разность хода

Δ = ± (2m+1)λ₀ /2 ( m= 1,2,3, …), (26.12)

то δ = ±(2m+1)π и колебания, возбуждаемые в точке обеими волнами, будут происходить в противофазе. Следовательно, (26.12) является условием интерференционного минимума.

Кольца Ньютона

Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного слоя, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.26.1).

Все рассуждения проведены для отраженного света. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхности воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей.

Запишем выражение для радиусов колец соответственно: m-^го-светлого кольца:

r_m = 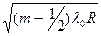, (m=0,1,2,3,…), (26.13)

m-^го- темного кольца:

r_m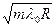^* = , (m=0,1,2,3,…). (26.14)

Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы) определить длину волны λ₀ и, наоборот, по известной длине волны λ₀ найти радиус кривизны линзы.

Система светлых и темных и полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску.

Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на λ₀/2, т. е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.

m- ^ое- темное кольцо:

r_m = 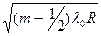, (m=0,1,2,3,…), (26.15)

m-^ое- светлое кольцо:

r_m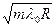^* = , (m=0,1,2,3,…). (26.16)