Множественная регрессия и корреляция
1. Добавление в уравнение множественной регрессии новой объясняющей переменной:
а) уменьшает значение коэффициента детерминации;
б) увеличивает значение коэффициента детерминации;
в) не оказывает никакого влияние на коэффициент детерминации.
2. Скорректированный коэффициент детерминации:
а) меньше обычного коэффициента детерминации;
б) больше обычного коэффициента детерминации;
в) меньше или равен обычному коэффициенту детерминации;
3. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
а) увеличивается;
б) уменьшается;
в) не изменяется.
4. Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
а) 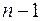 ;
;
б) 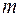 ;
;
в) 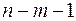 .
.
5. Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
а) 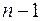 ;
;
б) 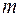 ;
;
в) 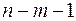 .
.
6. Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
а) 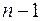 ;
;
б) 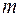 ;
;
в) 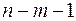 .
.
7. Множественный коэффициент корреляции 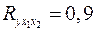 . Определите, какой процент дисперсии зависимой переменной
. Определите, какой процент дисперсии зависимой переменной 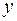 объясняется влиянием факторов
объясняется влиянием факторов 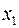 и
и 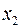 :
:
а) 90%;
б) 81%;
в) 19%.
8. Для построения модели линейной множественной регрессии вида 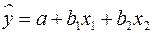 необходимое количество наблюдений должно быть не менее:
необходимое количество наблюдений должно быть не менее:
а) 2;
б) 7;
в) 14.
9. Стандартизованные коэффициенты регрессии 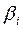 :
:
а) позволяют ранжировать факторы по силе их влияния на результат;
б) оценивают статистическую значимость факторов;
в) являются коэффициентами эластичности.
10. Частные коэффициенты корреляции:
а) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;
б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;
в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
11. Частный 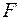 -критерий:
-критерий:
а) оценивает значимость уравнения регрессии в целом;
б) служит мерой для оценки включения фактора в модель;
в) ранжирует факторы по силе их влияния на результат.
12. Несмещенность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
13. Эффективность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
14. Состоятельность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
15. Укажите истинное утверждение:
а) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;
б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;
в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.
16. При наличии гетероскедастичности следует применять:
а) обычный МНК;
б) обобщенный МНК;
в) метод максимального правдоподобия.
17. Фиктивные переменные – это:
а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
б) экономические переменные, принимающие количественные значения в некотором интервале;
в) значения зависимой переменной за предшествующий период времени.
18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:
а) 4;
б) 3;
в) 2.
Дата добавления: 2016-01-29; просмотров: 1613;
