Отображения. Отношения.

Если каждому элементу хÎХ поставлен в соответствие некоторый элемент yÎY, то говорят, что определено отображение f множества Х во множество Y. Обозначают y=f(x). Элемент y есть образ элемента х при данном отображении f, х - прообраз элемента y и обозначают .

Частным случаем отображения множества Х во множество Y является отображение множества Х на множество Y. Отображение f множества Х в Y является отображение множества Х на Y, если каждому элементу yÎY был поставлен в соответствие какой-либо элемент хÎХ при данном отображении f. Такое соотношение называется сюръективным, т.е. если каждый элемент множества y имеет прообраз, то отображение f сюръективно.

Пусть X={a, b, c, d} Y={2, 4, 6}. Зададим отображения f₁ и f₂ так:

т.е.

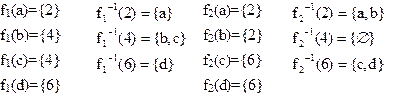
Отображение f₁ X в Y является сюръективным, т.е. отображением X на Y, т.к. каждый элемент множества Y имеет прообраз. Отображение f₂ несюръективно, элемент "4" не имеет прообраза.

Отображение X в Y называется инъективным, если для каждого элемента yÎY существует не более одного прообраза. Приведенные выше отображения f₁ и f₂ не являются инъективными.

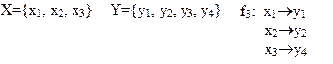
Отображение f₃ - инъективно.

Если отображение f сюръективно и инъективно, оно называется биективным (взаимнооднозначное соответствие).

Очевидно, биективное отображение между конечными множествами X и Y возможно только в случае, когда число элементов этих множеств совпадает.

Примером биективного отображения для бесконечных множеств может служить отображение f, установленное между множеством натурального ряда чисел A={1, 2, 3, ... n, ...} и множеством четных положительных чисел В={2, 4, 6, ...} по типу n«2n.

Рис.1

На рис. 1. показана возможность установления биективного отображения между множеством Z точек полуокружности и множеством Х точек открытого отрезка (а, b), а также между множеством Z и множеством Y точек прямой - множеством Y.

z, z₁ÎZ; Множества X, Y, Z - несчетные.

x, x₁ÎX;

y, y₁ÎY.

Упражнение 1.

Установить биективное отображение между множеством

A={1, 6, 11, 16, 21, ...} и натуральным рядом чисел.

Очевидно, это можно сделать, поставив в соответствие элементу натурального ряда "n" a_n=1+5(n-1)ÎA, т.е. n«1+5(n-1).

Упражнение 2.

Установить биективное отображение между множеством точек плоскости и множеством точек сферы, из которой выброшена одна точка.

Очевидно, это можно сделать геометрически (рис. 1.1.10):

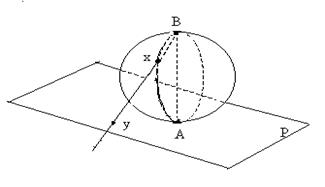
Рис. 2

Обозначим множество точек плоскости Р, множество точек сферы - М, точка А выброшена из сферы, xÎM, yÎP.

Чтобы установить биективное отображение между M и P достаточно соединить точку В лучом с точкой "х" и получить соответствующую точку "y", или точку В соединить с точкой "y" и получить соответствующую точку "х", т.е. "х"«"y".

Два множества называются количественно эквивалентными (или просто эквивалентными), если между ними можно установить биективное отображение.

Исходя из этого определения можно дать другую формулировку счетного множества: счетным называется множество, эквивалентное натуральному ряду чисел.

Очевидно, что справедливы следующие утверждения:

1. Конечные множества эквивалентны тогда и только тогда, когда они содержат одинаковое число элементов.

2. Два множества, порознь эквивалентные третьему, эквивалентны между собой.

3. Все счетные множества эквивалентны между собой.

4. Всякое множество, эквивалентное счетному множеству, счетно.

О двух эквивалентных множествах говорят, что они имеют одинаковую мощность.

Мощность - это то общее, что есть у эквивалентных множеств. Что общего имеют эквивалентные множества? Общим для них является число элементов. Мощность конечного множества есть число его элементов. Для бесконечных множеств является аналогом количества его элементов.

Все счетные множества имеют мощность, равную мощности натурального ряда чисел. Мощность натурально ряда чисел обозначается 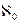- алеф-нуль.

Мощность континуума обозначается готической буквой C. Между этими мощностями существует следующая связь: .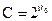

Как сравниваются мощности?

Рассмотрим два множества А и В. Если между ними можно установить биективное отображение, то мощности данных множеств равны. Если между множеством А и частью множества В можно установить биективное отображение, а между Множеством В и частью А нельзя, то мощность множества А меньше мощности множества В.

Для конечных множеств это положительно очевидно. Для бесконечных множеств оно также справедливо.

Мощность натурального ряда чисел - меньшая среди мощностей всех бесконечных множеств. Следующая по величине - мощность континуума. Пытаясь найти множество, мощность которого была бы промежуточной между мощностями континуума и натурального ряда чисел, Георг Кантор, основатель теории множеств, сформулировал так называемую гипотезу континуума - предложение, отрицающее множество промежуточной мощности. Попытки доказать это предложение привели к серьезным теоретическим исследованиям, связанным с пересмотром оснований математики.

Множества наибольшей мощности не существует, т.к. мощность множества подмножеств исходного множества всегда больше мощности исходного множества.

Упражнение 3

Доказать, что если А\В эквивалентно В\А, то А и В эквивалентны (рис. 1.1.11).

Решение: А=(А\В)ÈАÇВ

В=(В\А)ÈАÇВ

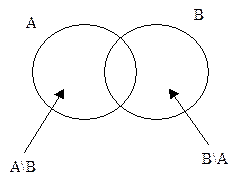
Рис. 3

Если (А\В) и (В\А) эквивалентны, то между элементами этих множеств существует биективное отображение. Элементы множества (АÇВ) поставим в соответствие самим себе. Следовательно, между элементами множеств А и В существует биективное отображение, т.е. А и В эквивалентны, т.е. мощности множеств А и В одинаковы.

Сформулируем некоторые основные теоремы, справедливые для счетных множеств.

Теорема 1.Всякая часть счетного множества есть либо конечное, либо счетное множество.

Теорема 2. Сумма конечного или счетного числа конечных или счетных множеств есть счетное множество.

Теорема 3. Всякое бесконечное множество содержит счетное подмножество.

Теорема 4. Если М - несчетное множество, а АÌМ есть конечное или счетное множество, то множества М и М\А эквивалентны.

Теорема 5. Присоединяя к некоторому бесконечному множеству М, счетному или несчетному, счетное или конечное множество А, получим множество МÈА, эквивалентное множеству М.

Теорема 6. Всякое бесконечное множество М содержит часть АÌМ, эквивалентную всему множеству М.

Теорема 7. Множество всех пар натуральных чисел счетно. Под парой натуральных чисел понимают два натуральных числа, расположенных в определенном порядке.

Теорема 8. Множество всех рациональных чисел счетно.

Теорема 9. Множество всех конечных последовательностей, составленных из элементов данного счетного множества, есть счетное множество.

Теорема 10. Множество всех алгебраических чисел счетно.

Теорема 11. Множество континуума несчетно.