Сила инерции. Принцип Д'Аламбера
В ряде случаев возникает необходимость описать движение, покой или равновесие тела, находящегося в неинерциальной системе отсчета. Например, требуется выяснить какие проблемы могут возникнуть у человека, находящегося в кабине космического корабля. Французский физик Д'Аламбер сформулировал простой принцип, позволяющий отвечать на вопросы о поведении тела в неинерциальной системе. Рассмотрим тело, которое находится в неинерциальной системе, движущейся относительно инерциальной системы с ускорением ас.
Векторная величина, равная произведению массы тела на ускорение системы и направленная в сторону, противоположную ускорению системы, называется силой инерции:
Fи=-m·ac. (8.1)
Сила инерции не является реальной силой, так как она не действует со стороны какого либо тела. Однако в неинерциальной системе ее можно (и нужно!) рассматривать, как обычную силу. При этом можно «забыть» о том, что система неинерциальна.
Д'Аламбер установил, что если ко всем реальным силам (действующим со стороны других тел) добавить силу инерции, то в неинерциальной системе можно использовать все законы и формулы, которые справедливы для инерциальных систем.
Пример
Пусть тело массой т подвешено на нити в кабине космического корабля, который стартует с Земли и поднимается вверх с ускорением «а».
Система отсчета, связанная с таким кораблем является неинерционной и к ней применим принцип Д'Аламбера (ускорение системы — это ускорение корабля: ас = а). На тело действуют сила тяжести со стороны земли (mg) и сила натяжения нити (Т) (рис. 8.1). Добавим к ним силу инерции Fи = т·а, которая направлена вниз (в сторону, обратную ускорению). Теперь можно описать покой тела относительно корабля: Т + mg + Fи = 0. Учитывая направления сил, получим уравнение для их величин: Т — mg — Fи = 0. Откуда найдем натяжение нити, удерживающей тело:
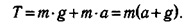
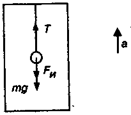
Рис.8.1. Использование силы инерции
Установлено, что сила инерции неотличимаот силы гравитации (силы тяготения). В рассматриваемом примере это означает, что никакие опыты, поставленные внутри корабля, не смогут дать ответ на вопрос, какая из ситуаций имеет место:
• либо мы находимся не в корабле, а на какой-то планете, где ускорение свободного падения равно g + a;
• либо мы движемся с ускорением g + а на космическом корабле вдали от каких-либо планет (гравитационные силы отсутствуют);
• либо мы стартуем с Земли, поднимаясь с ускорением «а». Во всех этих случаях результаты любого опыта будут совершенно одинаковы.
Дата добавления: 2015-11-28; просмотров: 857;
