Общие закономерности работы центробежных насосов

Центробежный насос состоит из корпуса, в котором вращается рабочее колесо с лопатками. Под действием возникающего центробежного поля жидкость отбрасывается от центра к периферии, так что вблизи оси насоса возникает разрежение, а на периферии давление возрастает. Схема рабочего колеса показана на рис. 2.1 (см. также рис. 2.3). На рис. 2.2 изображены планы скоростей жидкости для идеального центробежного насоса. На рис. 2.1 и 2.2 приняты следующие обозначения: индекс «1» соответствует точке входа на лопатку колеса, индекс «2» — точке выхода с лопатки; D — диаметр входа на лопатку (выхода с лопатки); b — ширина проточной части колеса; d — толщина лопатки; n — частота вращения рабочего колеса; u — вектор абсолютной скорости частицы (элемента) жидкости; u_от — вектор относительной скорости элемента жидкости (по отношению к лопатке); u_пер — вектор переносной скорости колеса (т. е. окружная скорость колеса); u_R — радиальная составляющая вектора абсолютной скорости элемента жидкости. Углы между касательными к лопатке и к окружности колеса: на входе β₁, на выходе — β₂. Углы между вектором абсолютной скорости u и касательной к окружности колеса: на входе — α₁, на выходе — α₂.

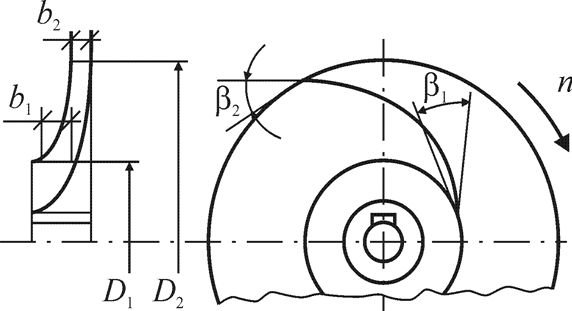
Рис. 2.1. Рабочее колесо центробежного насоса

Рис. 2.2. Планы скоростей: а) при входе жидкости в колесо; б) при выходе жидкости из колеса

При отсутствии специальных направляющих аппаратов подкрутка жидкости перед ее входом на лопатки рабочего колеса невелика, при этом скорость u₁ направлена радиально, т. е. α₁ = 90^о, u₁ = u_1R. Для достижения безударного входа жидкости на лопатки при заданной оптимальной подаче при конструировании центробежного насоса выбирают соответствующий угол β₁.

При бесконечно большом количестве лопаток с бесконечно малой толщиной теоретический напор насоса (формула Эйлера)

.Н_т = [u₂u_2перcosα₂ - u₁u_1перcosα₁]/g (2.1)

Если подкрутка отсутствует (α₁ = 90^о), то cos(α₁) = 0; тогда, используя выражение для подачи

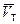= D₂b₂u_2R, (2.2)

теоретический напор можно выразить в виде

H_т = 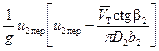. (2.3)

Действительный напор насоса меньше теоретического по следующим причинам: реальные лопатки имеют конечную толщину и их количество ограниченно, поэтому в межлопастных каналах колеса возникает циркуляция жидкости, план скоростей искажается; при течении жидкости в насосе (в межлопаточных каналах, при входе жидкости на лопатки, в улитке, во всасывающем и нагнетательном патрубках) неизбежны гидравлические потери. Первый фактор учитывают при помощи коэффициента циркуляции

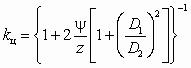, (2.4)

где ψ — коэффициент, зависящий от шероховатости поверхности проточной части колеса (принимают ψ = 0,9…1,1).

Второй фактор характеризуется гидравлическим КПД — h_г, который для современных гидравлических машин колеблется в пределах 0,80…0,96.

Действительный напор насоса можно рассчитать по формуле

Н = Н_т h _г k_ц. (2.5)

Действительная подача реального насоса с учетом толщины лопаток

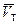= h_об k₂, (2.6)

где h_об — объемный КПД насоса; k₂ — коэффициент, учитывающий стеснение проточной части насоса лопатками: k₂ = (1 - zd)/(πD₂sinβ₂).

Отношение статического напора к полному для идеального насоса с безударным входом на лопатки (при оптимальном угле β₁)

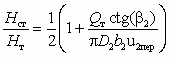, = (2.7)

причем H_σ/H_т = ½ при β₂ = 90^о. В реальных насосах для дости жения высокого КПД угол β ₂ выбирают в диапазоне 15…35^о (лопатки загнуты назад), при этом снижается скоростной напор, а значит, и гидравлические потери внутри насоса; помимо этого, соблюдение условия β₂ < 90^о позволяет избежать возникновения кавитации в зоне А (рис. 2.3). В ряде конструкций центробежных вентиляторов для достижения высоких скоростных напоров лопатки выполняют загнутыми вперед, т. е. β ₂ > 90^о, что приводит, однако, к снижению КПД.