Преобразователи кода.
Лекция Сумматор
Сумматором выполняется операция арифметического сложения двух многоразрядных двоичных чисел. Эта операция проводится по разрядам, что определяет целесообразным сначала рассмотреть принцип построения одноразрядного сумматора. Как видно из рис. 7.35,а, он имеет три ввода и два вывода. На два ввода Х и Y подаются логические “1” или “0”, соответствующие определенному разряду суммируемых чисел, а третий, Р0, предназначен для подачи логической “1”, если при суммировании предыдущего разряда будет его переполнение. На выводе Р сумматора будет “1” при переполнении разряда, который суммируется. В табл. 7.16 приведены возможные состояния одноразрядного сумматора.
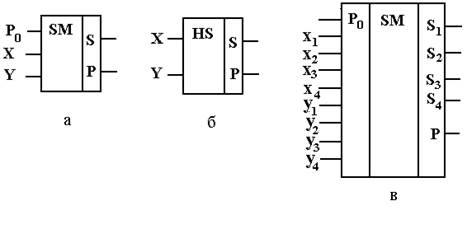
Рисунок 7.35. Схемное обозначение:
а - сумматора, б – полусумматора;
в - многоразрядного (четырехразрядного) сумматора
Таблица 7.16
| X | Y | P0 | S | P |
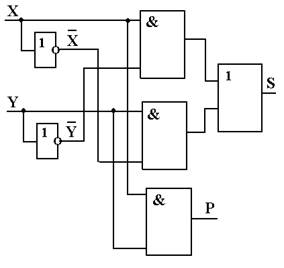
Рисунок 7.36. Схема полусумматора
В простейшем одноразрядном сумматоре, называемом полусумматором (рис. 7.35,б), отсутствует ввод Р0. Состояния полусумматора соответствуют данным табл. 7.16 при Р0 = 0. Согласно этой таблице для него функции S и Р от логических переменных Х и Y имеют вид:
S = X 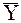 +
+ 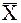 Y, Р =ХY. (7.15)
Y, Р =ХY. (7.15)
Следовательно, полусумматор может быть реализован на двух элементах “НЕ”, трех элементах “И” и одном элементе “ИЛИ”. Схема такой реализации представлена на рис. 7.36. На базе двух полусумматоров строится схема одноразрядного сумматора, как показано на рис. 7.37.
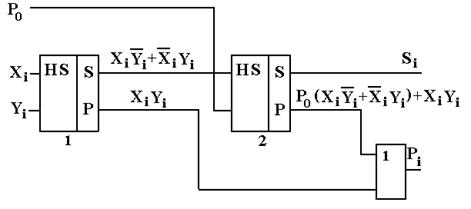
Рисунок 7.37. Схема сумматора
Действительно, согласно табл. 7.16,
Si = XiYi P0 + 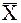 i Yi
i Yi 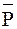 0 + P0 Xi Yi + P0 Xi Yi;
0 + P0 Xi Yi + P0 Xi Yi;
Pi = P0 (Xi 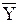 i +
i + 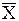 iYi) + XiYi.
iYi) + XiYi.
Эти соотношения с использованием тождеств алгебры логики могут быть преобразованы следующим образом:
Si = (Xi 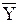 i +
i + 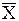 i
i 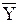 i)
i)  0 + P0 (
0 + P0 ( 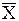 i
i 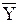 i + 0 + ХiYi + 0) =
i + 0 + ХiYi + 0) =
= (Xi 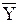 i +
i + 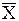 iYi)
iYi)  0 + P0 (Хi
0 + P0 (Хi 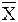 i + XiYi + Yi
i + XiYi + Yi 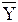 I) =
I) =
= (Xi 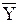 i +
i + 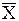 iYi)
iYi)  0 + P0 (
0 + P0 ( 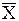 I + Yi) =
I + Yi) =
= (Xi 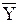 i +
i + 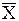 iYi)
iYi)  0 + P0
0 + P0 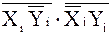 =
=
= (Xi 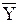 i +
i + 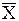 iYi)
iYi)  0 + (
0 + ( 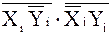 ) P0
) P0
Pi = P0 (Xi 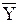 i +
i + 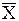 iYi) + XiYi (P0 +
iYi) + XiYi (P0 +  0) =
0) =
= P0 (Xi 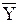 i +
i + 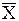 iYi) + XiYi ∙ 1 =
iYi) + XiYi ∙ 1 =
= P0 (Xi 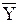 i +
i + 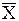 iYi) + XiYi.
iYi) + XiYi.
Из сравнения полученных соотношений с формулами (7.15) следует, что информация, снимаемая с клеммы S второго полусумматора, является результатом суммирования информации P0 и (Xi 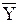 i +
i + 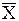 iYi), поступающих на его вход. Информация Рi является результатом логического сложения информации с клемм Р первого и второго полусумматоров.
iYi), поступающих на его вход. Информация Рi является результатом логического сложения информации с клемм Р первого и второго полусумматоров.
Для суммирования n-разрядных чисел используется n одноразрядных сумматоров, включенных по схеме рис. 7.38. На два входа каждого одноразрядного сумматора Xi и Yi подается информация, соответствующая определенному i-му разряду суммируемых чисел. На третий вход Р0 каждого такого сумматора, кроме первого, передается информация переноса с предыдущего сумматора (“1” в случае переполнения при суммировании в этом сумматоре). Ввод Р0 первого сумматора заземлен. Схемное обозначение многоразрядного сумматора приведено на рис. 7.35,в.
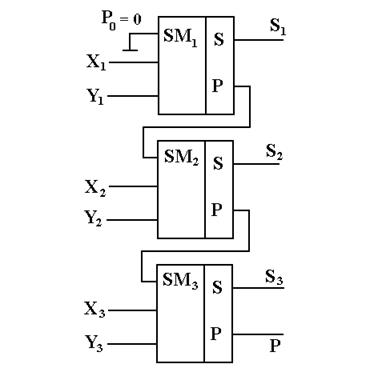
Рисунок 7.38. Схема трехразрядного сумматора
Многоразрядный сумматор можно использовать в качестве основы построения схем сравнения двоичных n-разрядных чисел, т.е. числового компаратора. Такая схема сравнения четырехразрядных чисел А и В приведена на рис. 7.39. Одно из этих чисел, например В, вводится в сумматор через логические элементы “НЕ”. Информация с вывода S сумматора подается на четырехвходовый логический элемент “И”. Таким образом, схема сравнения имеет два выхода: F – вывод элемента “И” и Р – вывод сумматора, фиксирующего переполнение последнего разряда при суммировании. При равенстве чисел А и В одинаковыми будут и числа в каждом их разряде, т.е. Аi = Вi. В соответствии с тождеством (7.2) алгебры логики (раздел 7.1) на всех выводах Si сумматора будут логические “1” и не будет переполнение всех разрядов при суммировании, т.е. Р = 0. Следовательно, на выходе схемы сравнения F = 1 и Р = 0. Если А ≠ В, то хотя бы в одном из разрядов этих чисел Аi ≠ Вi. Тогда при суммировании чисел таких разрядов с применением элемента “НЕ”, в схеме рис. 7.39, на выводах сумматора, соответствующих этим разрядам, будут логические “0”, что обусловливает появление “0” и на выходе логического элемента “И”.
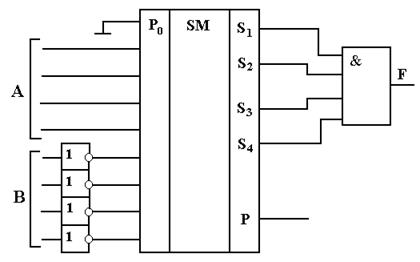
Рисунок 7.39. Цифровая схема сравнения двух четырехразрядных чисел
Преобразователи кода.
Дата добавления: 2016-01-20; просмотров: 782;
