Способы составления характеристического уравнения

Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
- непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
- путем использования выражения для входного сопротивления цепи на синусоидальном токе;
- на основе выражения главного определителя.
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 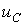 на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.
на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
 Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
jw заменяется на оператор р;
полученное выражение 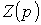 приравнивается к нулю.
приравнивается к нулю.
Уравнение
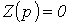
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника
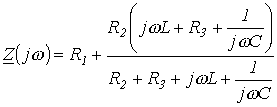 .
.
Заменив jw на р и приравняв полученное выражение к нулю, запишем
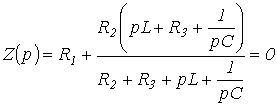
или
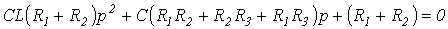 . .
| (1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
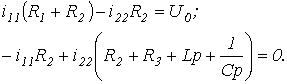
Отсюда выражение для главного определителя этой системы
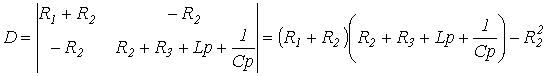 .
.
Приравняв D к нулю, получим результат, аналогичный (1).
Дата добавления: 2015-11-28; просмотров: 751;
