Модуляция на гармоническом переносчике
В качестве несущего колебания частот используют гармонические колебания вида:
u(t) = A(t) cos[ω(t)t + φ(t)]. (4.1)
В этом колебании переменной, как правило, может быть только одна величина – амплитуда A(t), частота ω(t) или фазы φ(t), две других величины (в простейших видах модуляции) должны оставаться неизменными. В зависимости от переменного параметра, выбранного для передачи информационного сигнала различают: амплитудную модуляцию (АМ) u(t) = A(t)cos(ω0t + l0), частотную (ЧМ) u(t) = A0 cos[ω(t)t + φ0] и фазовую (ФМ) u(t) = A0 cos[ω0t + φ(t)]. Следует отметить, что частотный и фазовый параметры гармонического колебания входят в состав более общего представления несущего колебания – u(t) = A0 cos Ψ(t) – в состав углового параметра гармонического сигнала, что привело к принятию более общего термина для ЧМ и ФМ – угловая модуляция. Рассмотрим виды модуляции на гармоническом несущем колебании. АМ –амплитудная модуляция непрерывным (аналоговым) сигналом, представляющим передаваемую информацию (например, телефонный сигнал в полосе 0,3÷3,4 кГц).
S(t) = A(t) cos (ω0t + φ0)
примем φ0 = 0,
S(t) = A0 + ∆Ax(t) = A0(1 + 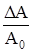 x(t)),
x(t)),
где А0 – начальное (среднее) значение амплитуды несущего колебания
cos ω0t;
∆А – возможное отклонение амплитуды несущего колебания.
Величину ΔА/А0 = m определим как параметр модуляции - глубина модуляции: 0 ≤ m ≤ 1. Обычно m измеряют в пределах 0% ≤ m ≤ 100%.
Модулированное по амплитуде колебание:
S(t) = A0[1 + m x(t)]cos ω0t. (4.2)
В качестве простейшего полезного информационного сигнала примем низкочастотный гармонический сигнал x(t) = cos Ω(t); Ω << ω0.
Теперь амплитуда модулированного колебания будет изменяться по закону передаваемого информационного сигнала x(t). Временное изображение АМ сигнала представлено на рис. 4.1.
 а)
а)
 б)
б)
Рис. 4.1.
Глубину модуляции можно измерить по максимальному и минимальному отклонениям амплитуды: 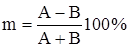 .
.
Преобразуем выражение для s(t) (4.2), раскрыв скобки:
S(t) = A0[1 + m cos Ωt]cos ω0t = A0 cos ω0t + A0 m cos Ωt cos ω0t =
= A0 cos ω0t + A0 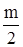 [cos(ω0 + Ω)t + cos (ω0 - Ω)t] = (4.3)
[cos(ω0 + Ω)t + cos (ω0 - Ω)t] = (4.3)
= A0 cos ω0t + 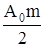 cos(ω0 + Ω)t +
cos(ω0 + Ω)t + 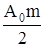 cos (ω0 - Ω)t.
cos (ω0 - Ω)t.
Исследуя полученное выражение, замечаем, что оно состоит из трех гармонических составляющих и каждая на своей частоте ω0, ω0+Ω, ω0-Ω. Построим графически полученное спектральное распределение составляющих (рис. 4.2).
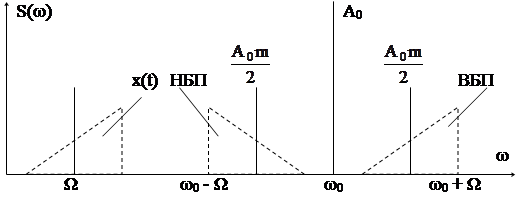 |
Рис. 4.2.
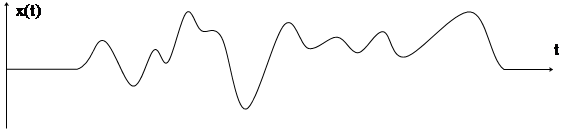
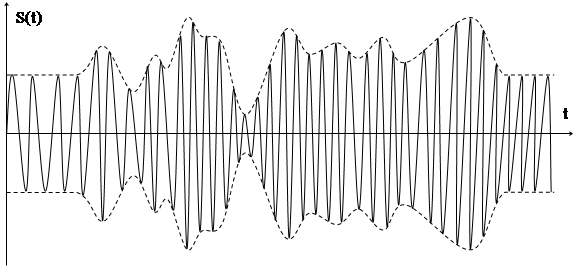
В случае модуляции несущей не гармоническим (тональным) сигналом, а белее сложным сигналом x(t) в полосе частот (например, телефонный сигнал в полосе 0,3÷3,4 кГц) получается более сложный спектр, состоящий из несущей и двух боковых полос: НБП - нижней боковой полосы и ВБП - верхней боковой полосы (нанесены пунктиром на рис. 4.2). На рис. 4.3. приведены временные графики произвольного телефонного сигнала (рис. 4.3а) и его модулированный вид (рис. 4.3б).
Несущее колебание на частоте ω0 имеет амплитуды А0, боковые составляющие равны А0m/2 и при m = 1 (100%), составляют А0/2. Несущее колебание имеет максимальную амплитуду, однако, не несет никакой полезной информации, поэтому в некоторых системах связи (при априори точном известном положении по оси частот сигнала несущей, что позволяет ее всегда восстановить на приемном конце) для экономии излучаемой энергии несущую можно не передавать - это системы сбалансной модуляцией - БМ (несущая необходима только при детектировании в качестве опорного колебания, относительно которого отсчитывают частоты боковых составляющих, поэтому в БМ несущую восстанавливают в приемнике по небольшому пилот-сигналу или известному кварцевому значению несущей). Обе боковые полосы несут информацию о модулирующем информационном сигнале x(t), располагаясь зеркально по частоте относительно несущего колебания. Для экономии энергии излучения и снижения занимаемой полосы частот можно передавать только одну боковую полосу - такая модуляция называется амплитудной модуляцией с одной боковой полосой АМ с ОБП.
 |
а)
 |
б)
Рис. 4.3
Амплитудная модуляция осуществляется в пределах схемы с нелинейными элементами (диоды, транзисторы с рабочей точкой на нелинейном участке характеристики), так как только с помощью нелинейного преобразования можно получить сигналы новых частот (или осуществить функцию перемножения двух сигналов, в результате чего образуются сигналы новых частот). Демодуляция должна проводиться тоже только на нелинейном элементе для получения (выделения) низкочастотной (модулирующей) составляющей АМ сигнала. Фильтрация низкочастной части спектра демодулированного сигнала фильтром низкой частоты выделяет информационный сигнал от высокочастотных компонент АМ сигнала.
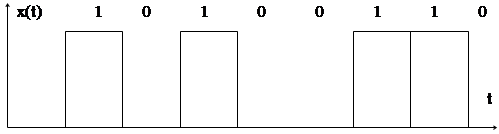
Пока мы рассмотрели амплитудную модуляцию при воздействии модулирующего сигнала x(t) - непрерывного (аналогового). Однако, подобные преобразования возможны и при импульсных последовательностях. Чаще всего встречается необходимость передачи бинарных сигналов, т.е. сигналов, имеющих два значения амплитуды
(0 и 1) (например, цифровые сигналы или сигналы в системе АЛС - автоматической локомотивной сигнализации). Модуляция несущего колебания бинарными информационными сигналами называется манипуляцией Мн или, иногда, применительно к амплитудной манипуляции - АТ - амплитудной телеграфией (АМн, АТ).
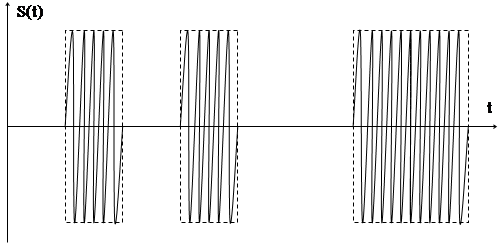
При воздействии на несущую информационным сигналом в виде последовательности прямоугольных импульсов (бинарных сигналов)
(рис. 4.4а) образуется промодулированная последовательность прямоугольных по огибающей радиоимпульсов, представленных на
рис. 4.4б.
Спектральный состав одного радиоимпульса рассмотрен в первой лекции и представлен на рис. 1.20. Здесь уместно повторить его на
рис. 4.5а.
 |
а)
 |
б)
Рис. 4.4
 |
а)
 |
б)
Рис. 4.5
Если последовательность радиоимпульсов регулярная, т.е. имеет постоянную скважность, то спектральный состав будет дискретным
(см. рис. 4.5б). При случайной последовательности ("телеграфный" сигнал) спектр последовательности будет содержать как сплошную, так и дискретную составляющие.
Понятие глубины модуляции при АМн отсутствует для бинарных символов, однако, его можно применить, если исходные импульсы имеют разную амплитуду.
Литература:
[1] стр. 61-73, 103-104. [2] стр. 88-96. [3] стр. 19-20.
Контрольные вопросы:
1. Какой параметр несущего колебания используется при АМ модуляции? Как ведут себя другие параметры несущего колебания при АМ?
2. Чем отличается манипуляция от модуляции?
3. Дайте определение видам модуляции БМ, ОБП.
4. Чем определяется ширина спектра АМ сигнала?
5. Что такое "глубина" модуляции АМ и как ее измерить?
Рассмотрим особенности угловой модуляции. Несущее колебание может передавать информационный сигнал изменением частоты или фазы несущего колебания:
S(t) = A0 cos Ψ(t) = A0 cos [ω(t)×t + φ(t)]. (4.4)
Изменение фазы связано с изменением частоты через зависимость:
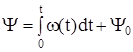 (4.5)
(4.5)
и соответственно
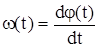 . (4.6)
. (4.6)
При исследовании частотной модуляции ω(t) для упрощения записи положи фазу φ(t) = 0. По аналогии с АМ изменение частоты:
ω(t) = ω0[1 + mωx(t)], (4.7)
здесь ω0 – основное (исходное значение частоты несущего колебания;
mω = ∆ω0/ω0;
∆ω – отклонение частоты (девиация частоты).
С учетом (4.5) и при Ψ0 = 0, а также (4.7) выражение (4.4) приводится к виду:
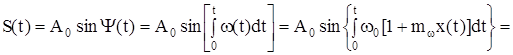
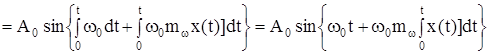 (4.8)
(4.8)
Как и ранее для АМ, в качестве простейшего сигнала, представляющего полезную информацию, примем низкочастотный гармонический (тональный) сигнал
x(t) = cos Ωt, Ω << ω0
Тогда выражение для частотной модуляции
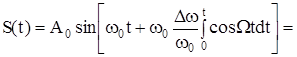
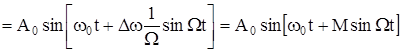 ,
,
здесь М = ∆ω/Ω – индекс модуляции, показывающий максимальное отклонение частоты (девиацию) несущего колебания при заданном (обычно 1000 Гц) значении частоты модулирующего колебания. Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω0, а определяется исключительно девиацией ∆ω и модулирующей частотой Ω.
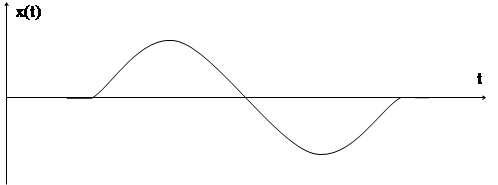
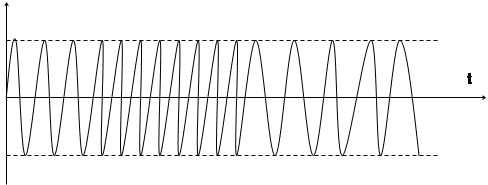
Временные графики ЧМ при модуляции гармоническим сигналом (4.6а) представлены на рис. 4.6б.
 |
а)
 |
б)
Рис. 4.6
Преобразуем выражения для частотной модуляции (для синуса сумма двух углов):
S(t) = A0 sin ω0t × cos [M sin Ωt] + A0 cos ω0t × sin [M sin Ωt] (4.9)
В теореме Бесселевых функций известны соотношения:
sin(M sin Ωt) = 2I1(M) sin 2Ωt + 2I3(M) sin 3Ωt + ...
cos(M sin Ωt) = I0(M) + 2I2(M) cos 2Ωt + 2I4(M) cos 4Ωt + ...
sin(M cos Ωt) = 2I1(M) cos 2Ωt - 2I3(M) cos 3Ωt + 2I5(M) cos 5Ωt - ...
cos(M cos Ωt) = 2I0(M) - 2I2(M) cos 2Ωt + 2I45(M) cos 4Ωt - ...
Ik(M) – функция Бесселя k-го порядка от аргумента М. График нормированных (приведенных по I0max = 1) приведен на рис. 4.7, а значения функций для разных М в табл. 4.1.
Таблица 4.1
| M | I0 | I1 | I2 | I3 | I4 |
| 0,0 | +1,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 0,5 | +0,94 | +0,24 | +0,01 | 0,00 | 0,00 |
| 1,0 | +0,76 | +0,44 | +0,11 | +0,02 | +0,002 |
| 2,0 | +0,22 | +0,58 | +0,35 | +0,13 | +0,003 |
| 3,0 | -0,26 | +0,34 | +0,48 | +0,31 | +0,13 |
| 4,0 | -0,39 | -0,06 | +0,36 | +0,43 | +0,18 |
| 5,0 | -0,18 | -0,33 | +0,04 | +0,36 | +0,39 |
| 10,0 | -0,25 | +0,04 |
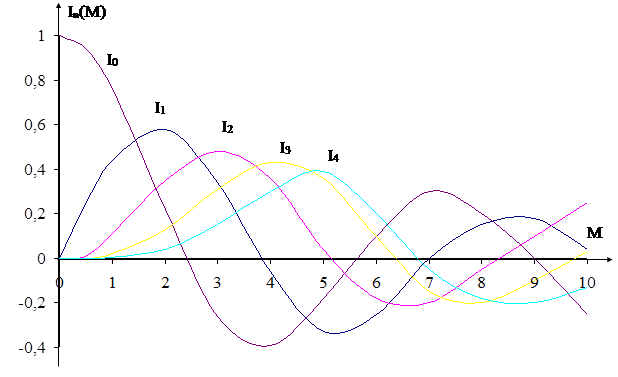
Рис. 4.7
Выберем из набора Бесселевых соотношений нужные для уравнения (4.9):
cos [M sin Ωt] = I0(M) + 2 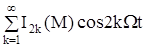 (4.10)
(4.10)
sin[M sin Ωt] = 2 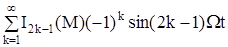 (4.11)
(4.11)
Тогда сигнал частотной модуляции представляется рядом:
 (4.12)
(4.12)
Спектральный состав ЧМ колебания оказывается достаточно сложным, состоящим из несущей и нескольких боковых составляющих выше и ниже по частоте относительно несущей и раздвинутых на Ω частоту модулирующего сигнала (см. рис. 4.8).
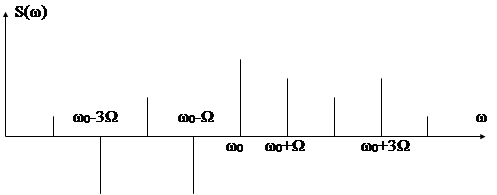 |
Рис. 4.8
Ширина спектра принципиально бесконечна, однако, если пренебречь составляющими с уравнением менее 1% от несущей, то ширина спектра сигнала определяется из выражения:
∆F = 2Fмод(1 + М + 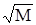 )
)
при М >> 1 можно пренебречь составляющей 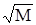 , и тогда
, и тогда
∆F = 2Fмод(1 + М),
при M < 1 в спектре остается только несущая и две боковых составляющих (рис. 4.9а).
Фаза спектральных составляющих, расположенных в нижней боковой полосе имеет для нечетных составляющих отрицательный знак (сдвинута по фазе на 180°) вследствие (4.11).
Если оценить спектр только по модулю, то спектр (рис. 4.9б) полностью совпадает со спектром АМ колебания (см. рис. 4.2).
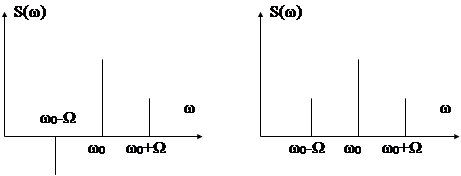 |
а) б)
Рис. 4.9
Литература:
[1] стр. 73-84. [2] стр. 96-102. [3] стр. 20.
Контрольные вопросы:
1. Дайте определение частотной модуляции.
2. Что такое "девиация"?
3. Что такое "индекс модуляции"? От чего он зависит и от чего не зависит?
4. Чем определяется ширина спектра ЧМ сигнала?
5. В чем отличие спектра ЧМ от АМ при малых (m < 1) индексах модуляции?
Фазомодулированный сигнал (ФМ)
S(t) = A0 sin [ω0t + φ(t)], (4.13)
у которого сдвиг фазы (по отношению с cos ω0t) изменяется от начального значения φ0 пропорционально модулирующему колебанию x(t):
φ(t) = φ0 + ax(t).
Теперь модулированный ФМ сигнал:
S(t) = A0 cos [ω0t + φ0 + ax(t)].
Так как мгновенное значение частоты является производной от фазы по времени (4.6), то при фазовой модуляции частота может быть определена в виде:
ω(t) = 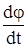 = ω0 + φ0 + a
= ω0 + φ0 + a 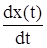 ,
,
т.е. фазомодулированный сигнал эквивалентен сигналу с частотной модуляцией с модулирующим сигналом 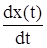 .
.
В случае, когда модулирующий информационный сигнал является, как и ранее, гармоническим (тональным), x(t) = U0 cos Ωt (Ω << ω0), полная фаза ФМ сигнала определяется равенством:
φ(t) = ω0t + φ0 + aU0 cos Ωt
а сам фазомодулированный сигнал:
S(t) = A0 sin[ω0t + φ0 + aU0 cos Ωt]. (4.14)
Величину aU0 = Мφ называют индексом фазовой модуляции. Так как наибольшее значение cos(Ωt + φ0) равно 1, то Мφ численно равно максимальному отклонению начального значения фазы колебания от среднего значения φ0.
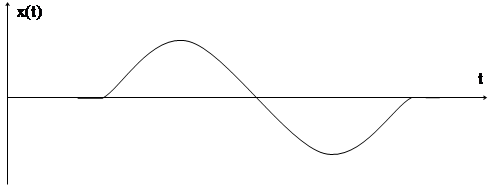
Временные характеристики ФМ колебания представлены на рис. 4.10 (а – модулирующий сигнал, б – модулированный).
Мгновенное значение частоты ФМ сигнала:
ω(t) = 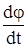 = ω0 -∆φΩ sin Ωt = ω0 -∆ω sin Ωt,
= ω0 -∆φΩ sin Ωt = ω0 -∆ω sin Ωt,
здесь ∆ω = ∆φΩ – девиация частоты ФМ колебания.
Спектральный состав ФМ колебания при гармонической модулирующей функции полностью совпадает со спектром ЧМ колебания при гармонической x(t); различить, где модуляция ЧМ, где ФМ невозможно.
 |
а)
 |
б)
Рис. 4.10
Иное положение при негармоническом модулирующем сигнале x(t). В этом случае вид модуляции можно установить по характеру изменения частоты и фазы во времени.
Покажем это на примере пилообразного модулирующего сигнала x(t).
Очевидно, что пилообразные изменения частоты ω(t) (рис. 4.11б), по форме совпадающие с x(t), свидетельствуют о наличии ЧМ, а такое же изменение φ(t) (рис. 4.11д) о наличии ФМ. Из рис. 4.11е – скачкообразные изменения частоты соответствует производной от пилообразного изменения фазы.
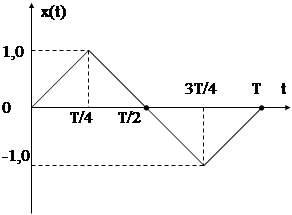 | 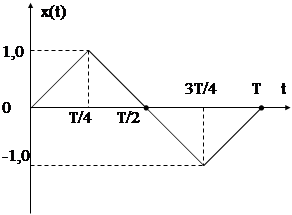 |
а) г)
 |  |
б) д)
 | 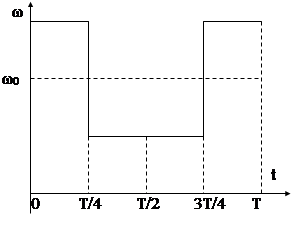 |
в) е)
Рис. 4.11
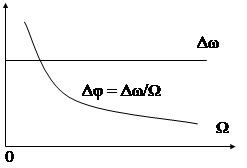
При ЧМ девиация ∆ω пропорциональна амплитуде модулирующего сигнала x(t) и не зависит от частоты модуляции Ω.
При ФМ величина ∆φ пропорциональна амплитуде x(t) и не зависит от частоты модуляции Ω.
На рис. 4.12 показаны зависимости индекса модуляции ∆ω т ∆φ от модулирующей частоты при ЧМ (см. рис. 4.12а) и ФМ (рис. 4.12б).
 |  |
а) б)
Рис. 4.12
ЧМ модуляция осуществляется изменением частоты автогенератора с помощью электронного конденсатора-варикапа (variable capacitor - переменная емкость) полупроводникового прибора с управляемой внешним напряжением емкостью p-n перехода.
ФМ модуляция осуществляется применением варикапа в контуре, расстроенном относительно частоты внешнего генератора, при этом изменение фазовой характеристики обусловлено установлением рабочей частоты на скате частотной характеристики колебательного контура.
Демодуляция ЧМ и ФМ сигналов производится в схемах, сравнивающих частоты и фазы приходящих сигналов с опорными колебаниями, вырабатываемыми в схемах демодуляторов.
Рассмотрим воздействия бинарных информационных сигналов при ЧМн и ФМн.
При частотной манипуляции изменяется скачкообразно частота в зависимости от значения бинарного сигнала (рис. 4.13).
В сигналах ЧМн или Чт (частотная телеграфия) стремятся к сохранению фазы колебания при переходе от одной частоты к другой. При этом помехоустойчивость системы ЧТ оказывается выше. Спектральный состав ЧМн сигнала оказывается композицией двух спектров со средними частотами ω1 и ω2. Составляющие спектра в общем случае подобны спектрам радиосигналов. Полоса частот спектра имеет расширение примерно на величину разности несущих частот двух бинарных радиосигналов.
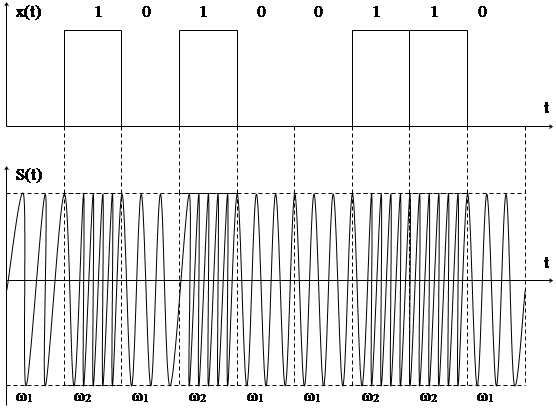 |
Рис. 4.13
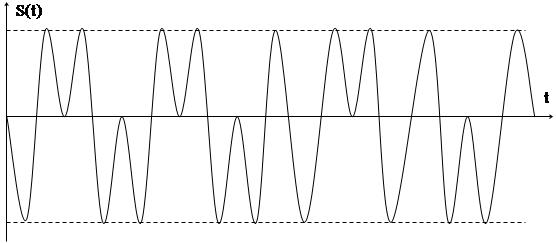
Особый интерес для систем связи представляют сигналы ФМн с фазовой манипуляцией (или ФТ – фазовая телеграфия). Применение в простейших системах двух сигналов, различающихся по фазе на 180° (противоположных) обеспечивает максимальную помехоустойчивость системы связи по сравнению с АМн и ЧМн ввиду использования наиболее различающихся сигналов (противоположных). Временная диаграмма ФМн приведена на рис. 4.14.

а)
 |
б)
Рис. 4.14
На рис. 4.14. фаза несущего колебания при передаче сигнала "1" равна 0° и для сигнала "0" равна 180°. В моменты перехода от "0" к "1" и наоборот наблюдаются перескоки фазы на 180°.
К сожалению, системы связи с ФМн обладают существенным недостатком, связанным с демодуляцией. Демодуляция должна осуществляться на основе сравнения фазы приходящего сигнала с фазой некоего опорного колебания. Его нужно либо передавать по отдельному каналу связи, что ведет к удвоению аппаратуры связи и использованию двух каналов связи, что крайне не экономично, потому и не используется, либо восстанавливать опорное напряжение в приемнике из принимаемой последовательности ФМн сигналов. Устройство формирования опорного напряжения (УФОН) строится по двум основным принципам: пассивные и активные. В пассивных УФОН (в частности схема Пистолькорса, рис. 4.15) для формирования опорного колебания с постоянной фазой используют метод удвоения частоты входящей последовательности (при этом вследствие применения процедуры двухполупериодного выпрямления для удвоения частоты значение фазы в 0° и в 180° теряется), последующее деление частоты на два приводит опорный сигнал к частоте, совпадающей с частотой входящего сигнала, но теперь уже без скачков фазы, с постоянной фазой.
На рис. 4.15 УРФ – узкочастотный (а значит, инерционный) резонансный фильтр, ФВ – фазовращатель (для компенсации возможных фазовых сдвигов в схеме УФОНа).
На рис. 4.16 приведена схема Сифорова – активного УФОН, в котором вспомогательный управляемый генератор УГ вырабатывает опорное напряжение, зависящее от сравнения в фазовом детекторе ФД фаз приходящего сигнала и УГ (сравнение производится на удвоенной частоте, на которой отсутствуют скачки фаз входного сигнала).
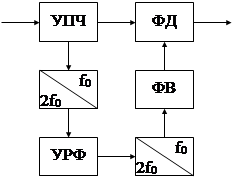 | 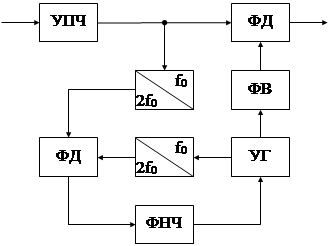 | ||
Рис. 4.15 Рис. 4.16
Кроме приведенных методов для восстановления опорного колебания в УФОН применяются активные схемы Костаса, также основанные на применении вспомогательного управляемого генератора совместно со схемами ФАПЧ – фазовой автоматической подстройки частоты, и некоторые другие.
Для всех приведенных методов создания УФОН присущ один серьезный недостаток – отсутствие начальной установки фазы, что может привести к приему сигналов "негативом". Такое явление, к сожалению, возможно и во время работы (перескок фазы) особенно при кратковременных пропаданиях сигнала.
Для устранения отмеченного недостатка русским ученым Петровичем Н.Т. был предложен метод передачи с использованием относительной фазовой манипуляции ОФМн (или ОФТ – относительная фазовая телеграфия). Метод ОФМн основан на сравнении фаз двух соседних посылок. Если передавалась "1", то фаза между посылками меняется на π, если "0", то фаза не меняется.
Такой принцип передачи цифровой информации позволяет демодулировать ОФМн сигнал без высоких требований к УФОНу. При этом возможны три способа демодуляции:
1. когерентный, при котором детектирование производится так же, как и для ФМн и в дальнейшем сравнение фаз производится по постоянному току;
2. некогерентный корреляционный, где также сравнение фаз двух посылок производится на постоянном токе после детектирования в квадратурных каналах;
3. автокорреляционный, в котором сравнение фаз двух соседних посылок производится на промежуточной частоте.
Дальнейшее развитие фазовых методов модуляции привело к созданию систем связи с многократными фазовыми сдвигами. Если в рассмотренной выше системе сдвиг фазы между двумя посылками принимался в 80°, то в двукратной ФМн возможна передача одновременно двух бит информации одной посылкой.
На рис. 4.17а изображена векторная диаграмма однократной ФМн (один из двух возможных положений вектора – посылки соответствуют передаче "0" или "1"), на рис. 4.17б изображена диаграмма двукратной ФМн (передается одна посылка–вектор, имеющая возможность принять одно положение из четырех возможных точек), при этом одной посылкой передается информация о двух битах информации. При применении ОФМн такая модуляция называется ДОФМн – двукратной относительной фазовой манипуляцией. По этому принципу возможно создание трехкратной ТОФМн, однако, с увеличением кратности фазовой манипуляции возрастают требования к точности фазового детектора, поэтому выше трехкратной модуляции не используют.
 | |||
 | |||
а) б)
Рис. 4.17
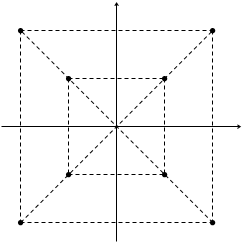
Фазовые методы манипуляции оказались весьма привлекательными ввиду их повышенной помехоустойчивости и относительной простоты модуляции и демодуляции. Развитие технической мысли привело к созданию конструкций сигналов с применением разных видов модуляций, позволяющих повысить скорость передачи информации за счет расширения информационных признаков у передаваемой посылки. Так, появился вид модуляции – КАМ – квадратно-амплитудная модуляция, которая объединила АМн и ОФМн, что значительно расширило число возможных изображающих точек в векторной диаграмме рис. 4.17 и позволило передавать одной посылкой (одним импульсом) 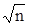 бит информации, где n – количество изображающих точек (и, соответственно, векторов) в векторной диаграмме сигнала. На рис. 4.18а приведено примерное временное изображение сигнала, а на рис. 4.18б – векторная диаграмма для модуляции КАМ-8.
бит информации, где n – количество изображающих точек (и, соответственно, векторов) в векторной диаграмме сигнала. На рис. 4.18а приведено примерное временное изображение сигнала, а на рис. 4.18б – векторная диаграмма для модуляции КАМ-8.
 | |||
 | |||
а) б)
Рис. 4.18
Ни рис. 4.18б – 8 изображающих точек (4 отличия по фазе и 2 отличия по амплитуде). Такая модуляция позволяет одним импульсом передать информацию о трех разрядах двоичного числа (или 3 бит) информационного цифрового сигнала. Максимально возможные конструкции на сегодня (по данным литературы) до КАМ-256, в котором одним импульсом передается информация о восьми разрядах двоичного информационного числа.
Литература:
[1] стр. 73-82, 103-114. [2] стр. 96-102. [3] стр. 20.
Контрольные вопросы:
1. Как связаны между собой ЧМ и ФМ модуляции?
2. Как определить отличие ЧМ и ФМ модуляции?
3. В чем отличие ОФМн от ФМн?
4. Дайте определение двукратной ОФМн.
5. Дайте определение КАМ модуляции.
Дата добавления: 2016-01-18; просмотров: 1525;
