Системы функций алгебры логики
Любая булева функция может быть представлена аналитически одной из вышерассмотренных нормальных форм, которые используют ограниченное число элементарных булевых функций. Например, для СДНФ такими функциями являются "конъюнкция", "дизъюнкция" и "отрицание". Следовательно, существуют системы булевых функций, с помощью которых можно аналитически представить любую сколь угодно сложную булеву функцию. Проектирование цифровых автоматов основано на знании таких систем булевых функций. Последнее особенно важно для определения набора элементарных логических схем, из которых можно построить произвольный цифровой автомат. Проблема функциональной полноты является центральной проблемой функциональных построений в алгебре логики.
Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булевых функций (f1, f2, ... fk), посредством которых можно записать произвольную булеву функцию f.
Это обусловливает целесообразность постановки задачи определения свойств, которыми должны обладать функции, составляющие ФПСБФ.
Решение этой задачи основано на понятии замкнутого относительно операции суперпозиции класса функций. Класс булевых функций, функционально замкнутый по операции суперпозиции, есть множество функций, любая суперпозиция которых дает функцию, также принадлежащую этому множеству. Среди функционально замкнутых классов выделяют классы обычного типа, называемые предполными, которые обладают следующими свойствами. Предполный класс S не совпадает с множеством Р всех возможных булевых функций, однако если в него включить любую не входящую в S булеву функцию, то новый функционально замкнутый класс будет совпадать с множеством Р. Проведенные исследования показали, что предполных классов пять, а для построения ФПСБФ необходимо и достаточно, чтобы ее функции не содержались полностью ни в одном из пяти предполных классов.
Наряду с нормальными формами представления функций алгебры логики в вычислительной технике широко используются логические полиномиальные формы. Преобразования над формулами булевых функций иногда удобно выполнять в алгебре Жегалкина. Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2, а также константу 1.
Теорема Жегалкина. Любая функция алгебры логики может быть представлена многочленом вида
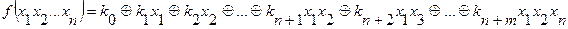 ,
,
где ki – коэффициент, принимающий значения 0 или 1.
Теорема позволяет представить любую ФАЛ в виде полиномов различной степени.
Задача построения полинома Жегалкина сводится к нахождению коэффициентов ki. Для любых конституент единицы k1 и k2 имеет место следующее соотношение: k1 + k2 = k1 Å k2. Оно позволяет выполнить переход от СДНФ к полиному Жегалкина. Для этого достаточно заменить в СДНФ символ + (дизъюнкции) на символ Å и выполнить подстановку вида х=х Å 1 с последующими преобразованиями в алгебре Жегалкина.
 Перечислим предполные классы булевых функций.
Перечислим предполные классы булевых функций.
Класс линейных функций. Функция алгебры логики называется линейной, если ее можно представить полиномом первой степени:
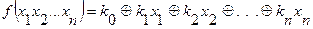 .
.
Примем без доказательства утверждение, что при суперпозиции линейных функций получаем линейную функцию. Существует восемь линейных функций от двух переменных (табл.10). Следовательно, в функционально полном базисе должна содержаться хотя бы одна нелинейная логическая функция.
Класс функций, сохраняющих ноль. К булевым функциям, сохраняющим константу 0, относят такие булевы функции f(x1,...,xn), для которых справедливо соотношение f(0,...,0)=0.
Класс функций, сохраняющих единицу. К булевым функциям, сохраняющим константу 1, относят такие булевы функции f(x1,...,xn), для которых справедливо соотношение f(1,...,1)=1.
Таблица 10
| k2 k1 k0 | f(x1x2…xn)=k0Åk1x1Åk2x2 | ||
| 0 0 0 | |||
| 0 0 1 | |||
| 0 1 0 | x1 | ||
| 0 1 1 | x1 Å 1 | ||
| 1 0 0 | x2 | ||
| 1 0 1 | x1 Å 1 | ||
| 1 1 0 | x1 Å x2 | ||
| 1 1 1 | 1 Å x1 Å x2 |
Класс монотонных функций. Функция алгебры логики называется монотонной, если при любом возрастании набора аргументов значения этой функции не убывают.Двоичный набор A=<a1,a2,...,an> не меньше двоичного набора B=<b1,b2,...,bn> , если для каждой пары (ai,bi) i = 1...n справедливо соотношение ai ≥ bi.
Если у двух наборов есть и большие и меньшие аргументы f(0,1) и f(1,0), то наборы считаются несравнимыми. Таким образом, если f(0,0)≥f(0,1) ≥ f(1,1) или f(0,0) ≥f(1,0) ≥f(1,1), то функция f является монотонной.
Класс самодвойственных функций. Булевы функции f1(x1,...,xn) и f2(x1,...,xn) называются двойственными друг другу, если выполняется соотношение 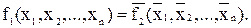
К самодвойственным булевым функциям относят такие булевы функции, которые двойственны по отношению к самим себе, то есть булева функция называется самодвойственной, если на любых двух противоположных наборах х1,х2,…,хn и 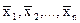 она принимает противоположные значения
она принимает противоположные значения 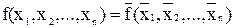 .
.
Любая ФАЛ, полученная с помощью операции суперпозиции и подстановки из функций одного класса, принадлежит этому же классу.
Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозиций исходных функций.
ТеоремаПоста−Яблонского. Для того чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
не являющуюся линейной;
не сохраняющую ноль;
не сохраняющую единицу;
не являющуюся монотонной;
не являющуюся самодвойственной.
Иначе говоря, система булевых функций является функционально полной тогда и только тогда, когда она целиком не содержится ни в одном из предполных классов.
Рассмотрим примеры ФПСБФ. Для удобства изложения материала сведем элементарные булевы функции двух переменных и некоторые функции одной переменной в таблицу (табл.11), классифицируя каждую из них по признакам принадлежности к предполным классам.
Таблица 11
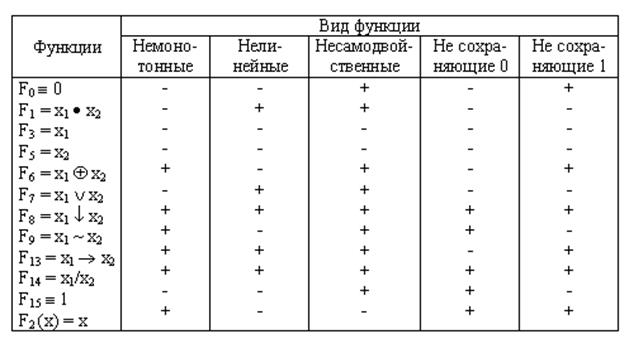
Из таблицы видно, что каждая из функций F8 и F14 является ФПСБФ. Иными словами, используя, например, только булеву функцию F14 - "штрих Шеффера", можно записать в виде формулы любую булеву функцию. Признаком функциональной полноты, очевидно, является наличие плюса в каждом столбце таблицы, хотя бы для одной из составляющих систему булевых функций. К таким ФСПБФ, наиболее распространенным в практике построения цифровых автоматов, следует отнести:
Дата добавления: 2016-01-09; просмотров: 1566;
