ПРИНЦИП ДЕЙСТВИЯ МИКРОВОЛНОВОДОВ

Основной структурой, предназначенной для передачи электромагнитного излучения в интегральной оптике, является тонкопленочный волновод. Он представляет собой аналог контактной металлизации электронных схем и выполняет функции информационных магистралей, по которым оптический сигнал направляется в ту или иную область пространства или часть схемы. Существуют планарные и трехмерные (канальные и полосковые) волноводы различной геометрии.

Трехмерные волноводы в отличие от планарных обеспечивают дополнительное ограничение излучения в поперечном направлении. Такое ограничение дает возможность значительно повысить степень локализации волноводного канала, что приводит к снижению управляющих напряжений волноводных модуляторов и переключателей, рабочих мощностей инжекционных лазеров, входящих в структуру интегрально–оптических схем. Применение трехмерных волноводных структур обеспечивает большую компактность и универсальность интегрально–оптических устройств за счет более высокой степени изоляции каналов друг от друга. Применение трехмерных волноводов расширяет функциональные возможности интегрально–оптических схем как за счет усложнения их схемотехнических конфигураций, так и за счет большего функционального разнообразия самих волноводных элементов, выполняемых на их основе (модуляторы и переключатели, излучающие структуры, многоканальные разветвители и др.).

Простейший планарный диэлектрический волновод представляет собой пленку прозрачного на данной длине волны диэлектрика, нанесенную на подложку из материала с более низким показателем преломления. Третьим слоем волновода (покровным) может служить воздух или любая другая среда. Чтобы удержать электромагнитную волну, показатель преломления волноводного слоя должен удовлетворять неравенствам

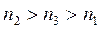, (7)

где n₃, n₁– показатели преломления соответственно материалов подложки и покровного слоя.

Если показатели преломления подложки и покровного слоя равны, такой волновод называется симметричным, в противном случае – асимметричным.

По степени локализации излучения волноводы делятся на планарные и трехмерные. В планарных область распространения света ограничена только в одном, вертикальном направлении – волноводный слой покрывает всю поверхность подложки и горизонтальный размер во много раз больше вертикального. В трехмерных волноводах оптический канал ограничен также и в поперечном направлении, так как горизонтальный размер волноводного слоя много меньше вертикального. В каждом конкретном случае выбор того или иного типа волновода определяется спецификой создаваемого прибора или устройства. Поэтому и планарные, и трехмерные волноводные структуры широко применяют в том большом разнообразии устройств, которым сегодня располагает интегральная оптика.

Как любая направляющая структура, интегрально–оптический волновод в первую очередь характеризуется набором электромагнитных колебаний (мод), которые могут распространяться в нем. Моду диэлектрического волновода на частоте w можно определить как решение волнового уравнения, которое имеет вид

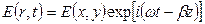, (8)

где 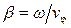– постоянная распространения, или фазовая постоянная; 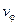– фазовая скорость волны. Решение этого уравнения должно удовлетворять условию непрерывности тангенциальных составляющих векторов Е и Н на границах раздела несущего диэлектрика, как со стороны покровного слоя, так и со стороны подложки.

Основные свойства диэлектрического волновода и их математическое выражение можно определить с помощью модели плоской пластины полубесконечной в направлении х или у (рис. 1). Трехмерные волноводы, размер которых ограничен в обоих направлениях, приближенно удовлетворяют модели планарного волновода, если один из размеров значительно больше другого.

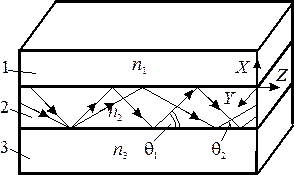Рис. 1. Структура диэлектрического волновода, 1 – покровный слой; 2 – волновод; 3 – подложка.

При заданной частоте w вид решения зависит от постоянной распространения b. Будем также считать, что выполняются неравенства (1), соответствующие распространенному случаю волноводной пленки, нанесенной на подложку с меньшим показателем преломления и с покровным слоем из воздуха. При выполнении неравенства

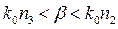(9)

решение в области волноводного слоя представляет собой гармоническую колебательную функцию, как это показано на рис. 2, в, б (область II), образуя в поперечном сечении волновода стоячую волну.

Полученные решения Е(х) удовлетворяют заданным граничным условиям, то есть и функция Е(х) и ее производная непрерывны на границе раздела. Энергия, переносимая такими типами колебаний, называемыми волноводными модами, заключена вблизи волноводного слоя. В областях I и III проникающее туда электромагнитное поле затухает экспоненциально. Поле на границах раздела волновод–подложка и волновод–покровный слой не обрывается резко до нуля. С одной стороны, это свидетельствует о том, что электромагнитная волна не полностью заперта в волноводе и, как следствие, часть энергии для потребителя (например, фотоприемника) теряется, что само по себе факт нежелательный. Иногда часть энергии, которая выходит за границу волноводного слоя и распространяется в приповерхностном слое, называют поверхностной волной. С другой стороны, наличие таких "хвостов" мод вне волновода необходимо для работы большого класса очень важных устройств интегральной оптики (таких, как элементы ввода и вывода, переключатели–модуляторы на связанных волноводах).

В зависимости от того, компонента какого поля – электрического или магнитного оказывается перпендикулярной направлению распространения волны, различают поперечные электрическую ТЕ_m– и магнитную ТМ_m– моды. Они отличаются числом вариаций поля по толщине волновода. Чем больше число т, тем выше порядок моды.

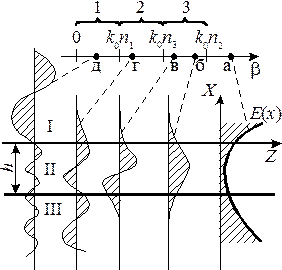Рис. 2. Распределение модовых полей в волноводе E(x) при различных постоянных распространения b: 1 – излучательные воздушные моды, 2 – излучательные моды подложки, 3 – волноводные моды.

Если моды распространения вдоль оси z (рис. 1), с координатной зависимостью амплитуды, пропорциональной exp(–ibz), то ТЕ– мода будет содержать только компоненты электромагнитного поля Е_у, Н_х, Н_z, а ТМ — Н_у, Е_х, Е_z. В первом случае в поперечной плоскости волновода оказывается ограниченным электрическое поле волны, во втором – магнитное. Это определяет различные режимы работы волноводных структур. Свойства ТЕ и ТМ волноводных мод в общем случае очень схожи, но есть и ряд различий. Фазовый сдвиг при полном внутреннем отражении и фазовая скорость у ТМ мод больше, чем у ТЕ. Волноводные моды – основные рабочие моды устройств интегральной оптики. Необходимое условие существования волноводных мод – выполнение неравенства

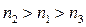, (10)

откуда следует, что внутренний слой волноводной структуры должен обладать более высоким показателем преломления, чем внешние слои I и III.

При выполнении неравенства 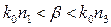решение волнового уравнения имеет экспоненциальный характер в области I и гармонический в областях II, III (рис. 2, г). Этот тип колебаний называется излучательными модами подложки. Они могут поддерживаться волноводной структурой, но из–за непрерывных потерь энергии за счет ее перекачки из волноводного слоя в подложку быстро затухают в ней по мере распространения. Как правило, использовать эти моды для передачи сигнала не представляется возможным.

Если постоянная распространения лежит в интервале от нуля до k₀n₁ (рис. 2, д), решение будет иметь колебательный характер во всех трех областях. Этот случай соответствует излучательным воздушным модам, но такое излучение быстро затухает. Излучение происходит и на границе с подложкой. Этот тип мод (аналогично предыдущим) из–за отсутствия локализации излучения в волноводном слое не может быть использован для передачи сигнала.

Наконец, последний случай, когда выполняется неравенство b > k₀n₂. Здесь решение волнового уравнения должно иметь экспоненциальный характер во всех областях. Единственная форма моды, удовлетворяющая этому условию, показана на рис. 2, а. Такой тип колебаний на практике реализовать нельзя: поле неограниченно возрастает в областях подложки и покровного слоя, что требует приложения бесконечно большой мощности.

Анализ решения системы волновых уравнений, удовлетворяющих граничным условиям на поверхности раздела, показывает, что в режиме волноводных мод спектр постоянных распространения дискретный, а излучательным модам принадлежит континуум (непрерывный спектр) b. Число волноводных мод зависит от толщины волновода h, частоты w и показателей преломления сред, образующих волновод. При данной частоте число волноводных мод растет с увеличением толщины волноводной пленки.

Величина постоянной распространения представляет собой проекцию волнового вектора, и, следовательно, каждому ее значению соответствует волна, распространяющаяся в волноводе под определенным углом q. Плоские волны, соответствующие разным модам, падают под разными углами q_m на поверхности разделов пленка – подложка, пленка – покровный слой, причем эти углы могут принимать не любые, а строго определенные значения в диапазоне

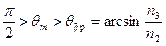. (11)

Значения углов q_m находятся из условия равенства суммарного изменения фазы волны за один проход через волноводную пленку, кратного 2p. Это изменение фазы складывается из ее скачков при отражении плоской волны от границ пленка – окружающая среда и набега фазы при прохождении волны в объеме волноводной пленки.

В случае волноводных мод часть поля волны все же проникает в подложку и покровный слой. В связи с этим при анализе волноводных структур часто используют понятие эффективной толщины волновода, под которой понимают либо ту часть, в которой переносится 99 % всей электромагнитной энергии, либо величину, равную геометрической толщине волновода, увеличенную на сумму , где

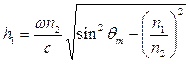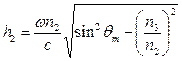; ; (12)

В терминах геометрической оптики увеличение эффективной толщины волновода означает, что пересечение световых лучей происходит не на действительных границах между волноводом и подложкой и покровным слоем, а на расстояниях 1/h₁ и 1/h₂ от них. Этот эффект носит название эффекта Гуса – Хэнхена. Так как h₁ и h₂ прямо пропорциональны частоте световой волны w, то по мере уменьшения w влияние проникновения поля за пределы волновода на величину эффектного сечения увеличивается. Для любой волноводной моды с т > 1 существует определенная минимальная частота отсечкиw_C, для которой при всех частотах, меньших w, волноводный эффект отсутствует. Эта частота соответствует длинноволновой отсечке l_C. Поскольку на практике чаще всего длина волны излучения фиксирована, проблема отсечки приобретает несколько другой смысл: какими должны быть показатели преломления волноводной структуры, чтобы в ней могла распространяться заданная мода? Для симметричного волновода, когда n₁ = n₃, необходимая величина скачка показателя преломления

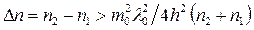, (13)

где m₀ = 0, 1, 2, 3. Если n₃ >> n₁ и n₂ @ n₃ то режим отсечки ограничен неравенством

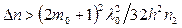. (14)

Из приведенных соотношений следует, что изменение показателя преломления, необходимое для поддержания мод нужного порядка, мало. Так, например, для n₂ = 3,6 достаточно иметь Dn @ 10^–2.

Для того чтобы в волноводе могло распространяться несколько мод, критическая толщина волновода при увеличении номера моды на единицу должна возрасти на величину 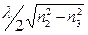. Отсюда можно оценить максимальное число мод М, которые могут существовать в диэлектрическом волноводе данной толщины

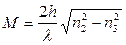. (15)

В интегральной оптике ограничение светового канала в одной плоскости ухудшает согласование микроволноводов с другими компонентами и стекловолоконными световодами и кабелями, осложняет локализацию оптических связей, снижает эффективность волноводных устройств. Большими степенями свободы характеризуются трехмерные волноводы, которые получили основное распостранение в интегральной оптике. Основные типы трехмерных интегральных волноводов схематически представлены на рис. 3. Деление трехмерных волноводов на полосковые и канальные в некоторой степени условно, тем не менее, оно отражает конструктивные особенности структур, влияющие на возможное число волноводных мод, специфику распределения полей и, следовательно, на основные их характеристики.

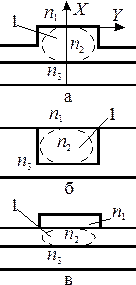Рис. 3 Основные типы трехмерных волноводов: а, б – канальные; в – полосковый; 1– область оптического канала.

В канальных волноводах гребенчатого типа (рис. 3, а) значительный скачок показателя преломления в поперечном направлении, как правило, приводит к многомодовому их режиму. Погруженные канальные структуры (рис. 3, б) характеризуются промежуточными свойствами по сравнению с гребенчатыми канальными и полосковыми волноводами. Число распространяющихся мод в них определяется размером канала и разностью показателей преломления материалов, образующих волновод.

Полосковый волновод, или волновод с налаженной полоской (рис. 3, в), представляет собой планарный тонкопленочный или диффузионный волновод с узкой диэлектрической областью, нанесенной на его поверхность. Здесь практически вся световая мощность локализована под полоской диэлектрика и почти не проникает в нее. В результате неровности границ раздела между полоской и волноводом не приводят к значительным потерям излучения. В полосковых волноводах легко реализуется одномодовый или маломодовый режим работы,

Наиболее перспективны для интегральной оптики полосковые и погруженные канальные волноводы. Основные их достоинства связаны с широкими технологическими и конструктивными возможностями создания эффективных волноводных структур на их основе. К положительным характеристикам полосковых структур следует отнести слабую чувствительность к нарушениям границ диэлектрической полоски и увеличение допуска на ее формат в одномодовом режиме. В интегрально–оптических схемах ее ширина может достигать десяти и более микрометров, что в значительной степени упрощает операцию стыковки волноводов.

В зависимости от назначения, волноводные структуры, в интегральной оптике выполняются либо на пассивных, либо на активных подложках. В последнем случае волновод становится управляемым, что дает возможность выполнять на основе волноводных компонент модуляторы, переключатели, ответвители и другие элементы интегральной оптики.

Для выполнения пассивных волноводных функций используются, как правило, волноводы на стеклянных подложках. Это обусловлено относительной простотой изготовления оптических элементов в таких волноводах и стыковки их с оптическими волокнами, а также доступностью и низкой стоимостью исходного материала.