Звукоизоляция одинарных ограждений
Так как эффект изоляции звука основан на его отражении, то для изоля-ции звука в воздухе, т.е. в среде с малым акустическим сопротивлением, следу-ет применять преграды из материалов с большим акустическим сопротивлени-ем (металлы, дерево, твердые пластмассы).
Коэффициент прохождения звука τ, падающего нормально на границу двух сред можно определить по коэффициенту отражения η, который определя-ется через акустические импедансы Z граничащих сред
| η = [(Z1 - Z2)/ (Z1 + Z2)]2 | (4.5) |
В твердых звукоизолирующих ограждениях поглощение энергии в мате-риале существенно меньше, чем отражение (α << η). Тогда выражение (4.3) примет вид δ + τ = 1, и коэффициент прохождения можно определить как
| τ = 1 – η = 1 - [(Z1 - Z2)/ (Z1 + Z2)]2 = 4Z1 Z2 / (Z1 + Z2)2 | (4.6) |
Если звуковая волна, распространяющаяся в воздушной среде, встречает препятствие в виде массивной перегородки, то Z1= ρc, а импеданс Z2 включа-ет как инерционное сопротивление на единицу ее площади, так и волновое со-противление среды за стенкой, т.е.
| Z2 = jωm + ρc | (4.7) |
тогда с учетом (4.6)
τ = 1 – mod [ - jωm / (2ρc+ jωm)]2
Проделав несложные преобразования, получим
| τ = 1 / [1+(ωm/2ρc)2] | (4.8) |
Принимая во внимание, что ω = 2πf из (4.4) получим для звукоизоляции
| R = 10lg(1/ τ) = 10lg [1+( πf m / ρc)2] | (4.9) |
При достаточно больших значениях произведения f m
| R ≈ 20lg ( πf m / ρc) ( f ≠ 0) | (4.10) |
Формула (4.10) известна под названием "закон массы".
При косом падении звуковой волны на перегородку под углом θ к норма-
| ли импеданс препятствия будет Z = jωm cos θ , а звукоизоляция | |
| R = 10lg(1/ τ) = 10lg [1+( πf m cos θ / ρc)2] | (4.11) |
Как видно, звукоизоляция перегородки при косых углах падения умень-шается, хотя на первый взгляд можно было бы предположить обратное. Это яв-ление называется компонент - эффектом и наблюдается на частотах, на кото-рых перегородка является твердой, т.е. ее изгибная жесткость не проявляется.
В реальных условиях звуковое поле, воздействующее на перегородку, яв-ляется диффузным, т.е. в нем все углы падения звуковых волн на перегородку равновероятны.
Это уменьшает звукоизоляцию, по мнению ряда исследователей на вели-чину = 5 дБ. Тогда, подставляя численные значения π и ρc для воздуха, полу-чим из (4.10)
| R = 20 lg f m – 47,5 ( дБ) | (4.12) |
здесь m - масса 1м2 ограждения.
Из (4.12) следует, что при увеличении частоты или массы вдвое звуко-изоляция увеличивается на 6 дБ. Таким образом, звукоизоляция увеличивается на 6 дБ в каждой последующей октавной полосе.
Закон массы нарушается на частотах близких к критической частоте пре-грады, т.е. когда имеет место резонанс совпадения. Как уже отмечалось ранее при рассмотрении вопроса о звукоизлучении, это явление возникает при совпа-дении длин изгибных волн в пластине и в воздушной среде. На этих частотах начинается звукоизлучение пластин в дальнее поле. Аналогично происходит и при падении звуковой волны на препятствие. Если длины волн в воздушной среде и в пластине совпадают, то препятствие становится «прозрачным» для такого звука и волна почти беспрепятственно проходит через него. Ранее было показано, что критическая частота, соответствующая равенству волн, определя-ется
| f | = | c2 | 12ρ( 1 − µ2 ) / Е | , | (4.13) | |||
| кр | 2πh | |||||||
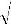
где h –толщина пластины, E –модуль Юнга, µ – коэффициент Пуассона мате-риала пластины.
В диффузном звуковом поле всегда найдутся такие углы, для которых выполнится условие совпадения λ/sin θ = λизг. Поскольку таких углов много, то уменьшение звукоизоляции начинается уже с частоты f > 0.5fкр.
На частотах f > 2fкр существенное значение начинает играть жесткость ограждения и внутренние потери η. Звукоизоляция шарнирно опертой пласти-ны
| R = 20 lg ( πf m / ρc) + 5 lg f/ fкр +10 lg η | (4.14) |
На этих частотах звукоизоляция вновь начинает увеличиваться примерно на 7,5 дБ при удвоении частоты.
Общий вид частотной характеристики звукоизоляции однослойных огра-ждений показан на рис.4.2.

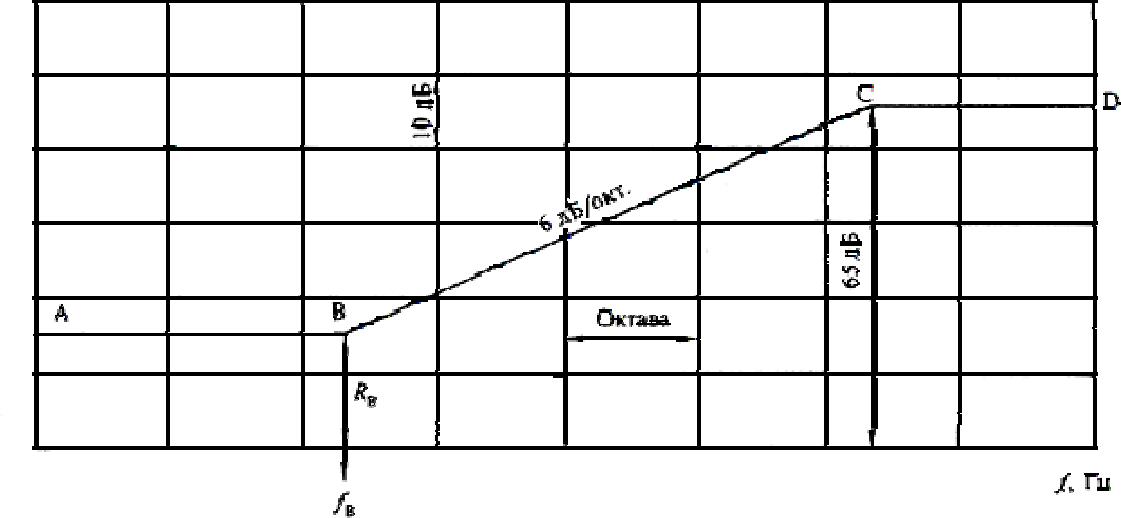
Рис. 4.2. Частотная характеристика изоляции воздушного шума однослойным плоским ограждением
Меняя цилиндрическую жесткость ограждения, можно изменять величи-ну критической частоты, а следовательно и эффективность звукоизоляции в том или ином диапазоне. Так, уменьшение жесткости смещает область пониженной звукоизоляции в высокочастотную часть спектра. При увеличении жесткости граничная частота снижается, что целесообразно при достаточно толстых огра-ждений с fкр < 300 Гц. А для тонких перегородок усиление их ребрами жестко-сти может привести к ухудшению из звукоизолирующих способностей на низ-ких и средних частотах.
Если стеновые (панельные) материалы имеют сквозные поры,– ЗИ резко снижается. Закрытие пор, штукатуркой или окрашиванием, снимает их влия-ние. Крупные пустоты могут привести к снижению ЗИ из-за резонансных коле-баний воздуха в полостях. Элементы строительных конструкций из таких ма-териалов, например крупнопористого бетона, должны иметь наружные слои из плотного бетона или раствора толщиной не менее 2 см.
Дата добавления: 2016-01-03; просмотров: 1455;
