Происхождение десятичной Системы Счисления
Непозиционные Системы Счисления
Кроме позиционных, существуют и другие – непозиционные системы счисления, построенные на иных принципах.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Общеизвестным примером такой системы является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
| I | V | X | L | C | D | M |
В этой системе имеется некоторый набор основных символов и каждое число представляется как комбинация этих символов; смысл каждого символа не зависит от места котором он стоит.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются:
| VI = 5 + 1 = 6 | LX = 50 + 10 = 60 |
Если же слева записана меньшая цифра, а справа большая, то их значения вычитаются:
| IV = 5 – 1 = 4 | XL = 50 – 10 = 40 |
Рассмотрим числа:
а) LXXXVII = (50 + 30) + (5 + 2) = 87. В данном примере цифра Х, участвуя 3 раза, каждый раз означает одну и ту же величину – 10 единиц.
б) MCMXCVI = 1000 + (1000 - 100) + (100 - 10) + (5 + 1) = 1996
Римские цифры мы часто встречаем и сейчас, например, на  циферблатах часов, в книгах при нумерации глав, в обозначении веков. Однако, в математической практике они не применяются. Позиционные системы удобны тем, что позволяют записывать большие числа с помощью сравнительно небольшого количества знаков. Еще более важное преимущество позиционных систем – это простота и легкость выполнения арифметических операций над числами. Попробуйте для сравнения перемножить два трехзначных числа, записав их римскими цифрами.
циферблатах часов, в книгах при нумерации глав, в обозначении веков. Однако, в математической практике они не применяются. Позиционные системы удобны тем, что позволяют записывать большие числа с помощью сравнительно небольшого количества знаков. Еще более важное преимущество позиционных систем – это простота и легкость выполнения арифметических операций над числами. Попробуйте для сравнения перемножить два трехзначных числа, записав их римскими цифрами.
Происхождение десятичной Системы Счисления
Всем нам эта система знакома с первого класса. Мы знаем этот ряд чисел от 0 до 9. Почему именно числу 10 отведена такая привилегированная роль? Человек, далекий от этих вопросов, ответил бы, вероятно, не задумываясь, так: дело просто в том, что число 10 – круглое, на него удобно умножать, любое число, поэтому удобно считать десятками, сотнями и т. д. Дело обстоит как раз наоборот: число 10 потому и круглое, что оно принято за основание системы счисления. При переходе к какой-либо иной системе счисления, скажем семеричной, где оно записывается в виде (13)7, его «круглость» немедленно исчезнет.
Причины, по которым именно десятичная система оказалась общепринятой, совсем не математического характера. Десять пальцев рук – вот тот первоначальный аппарат для счета, которым человек пользовался, начиная с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т. е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу (единицу следующего разряда). Десять десятков составляют единицу третьего разряда и т. д. Таким образом, именно счет по пальцам рук положил начало той системе, которая кажется нам сейчас чем-то само собой разумеющимся.
Появилась десятичная система, вероятно, в Индии. Выбор графических изображений для цифр, разумеется не принципиален. Современные изображения цифр - простая стилизация древних арабских цифр. Марокканский историк Абкелькари Боужибар считает, что арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры. В самом деле, если посмотреть на рисунок, это предположение кажется не лишенным глубокого смысла.
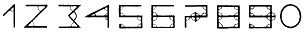
Так, единица создает лишь один угол, тройка - три, пятерка - пять и т.п. нуль не образует никакого угла, поэтому он не имеет никакого содержания.
Дата добавления: 2016-01-03; просмотров: 930;
