Коэффициент полезного действия (кпд) машины
Энергия, потребляемая машиной, расходуется на преодоление полезных и вредных сопротивлений. Полезные – это сопротивления, для преодоления которых машина предназначается. Вредные – это сопротивления, преодоление которых не даёт производственного эффекта.
Механическим КПД ( 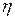 ) называется отношение полезной работы
) называется отношение полезной работы 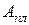 или мощности
или мощности 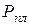 к затраченной
к затраченной 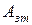 (
( 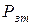 ). Потери механической энергии в разного рода устройствах состоят главным образом из потерь на трение:
). Потери механической энергии в разного рода устройствах состоят главным образом из потерь на трение:
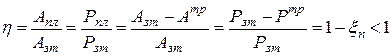 ,
,
где 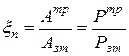 - коэффициент потерь.
- коэффициент потерь.
При холостом ходе машины 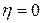 , но могут быть случаи когда
, но могут быть случаи когда 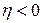 , что означает невозможность совершать движение из-за явления, называемого самоторможением. Например, червячный редуктор не может совершать вращение со стороны червячного колеса.
, что означает невозможность совершать движение из-за явления, называемого самоторможением. Например, червячный редуктор не может совершать вращение со стороны червячного колеса.
Рассмотрим машину как совокупность n элементов, соединённых различным образом между собой.
1. Элементы соединены последовательно и кпд ( 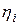 ) каждого из них известны (рис. 95, а). Тогда
) каждого из них известны (рис. 95, а). Тогда
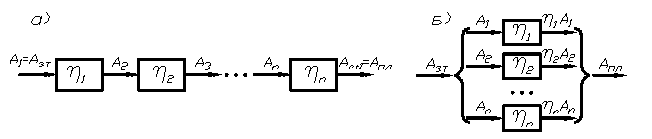
рис. 95
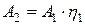 ;
; 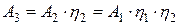 ; …
; … 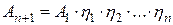 ,
,
т.е. общее кпд всей цепи равно:
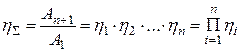
Поэтому следует стремиться к созданию простых конструкций с малым числом элементов.
2. Элементы соединены параллельно (рис. 95, б). Тогда
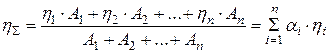 ,
,
где 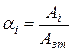 - коэффициент распределения энергии.
- коэффициент распределения энергии.
При 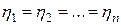 получим
получим 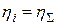 , следовательно низкое качество отдельных элементов меньше влияет на общее кпд машины, чем при последовательном соединении.
, следовательно низкое качество отдельных элементов меньше влияет на общее кпд машины, чем при последовательном соединении.
Сложные механизмы могут образовывать разветвлённую систему, состоящую из последовательного и параллельного соединённых более простых механизмов, где кпд определяется согласно указанным выше правилам.
Так как любой механизм представляет собой кинематическую цепь с последовательно и параллельно соединёнными в кинематических парах звеньями, то общее кпд механизма вычисляется аналогично при известных кпд кинематических пар.
 Например, необходимо определить
Например, необходимо определить 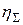 механизма с низшими парами, изображённого на рис. 96.
механизма с низшими парами, изображённого на рис. 96.
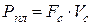 - мощность сил полезного сопротивления;
- мощность сил полезного сопротивления;
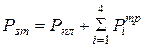 -затраченная мощность.
-затраченная мощность.
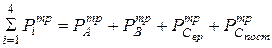 .
.
рис. 96
Мощность, затраченная на трение в кинематических парах, равна:
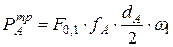 ;
; 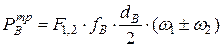 ;
;
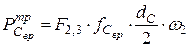 ;
; 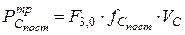 ,
,
где 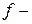 коэффициенты трения в парах;
коэффициенты трения в парах; 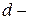 диаметры шарниров во вращательных парах. Мгновенный кпд, который является функцией положения звена 1, равен:
диаметры шарниров во вращательных парах. Мгновенный кпд, который является функцией положения звена 1, равен:
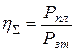 .
.
Дата добавления: 2015-12-29; просмотров: 671;
