Несгрупированый ряд Сгруппированный ряд

1-й показатель-размах вариации отклонение максимального признака от минимального
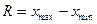
2-й показатель – среднее линейное отклонение – представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их среднего значения.
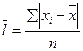
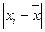- это абсолютное значение (модель) отклонения значения варианты от ее ср. величины.
3-ий показатель – дисперсия – представляет собой средний квадрат отклонений вариант от их среднего значения.
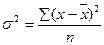
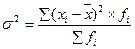
4-ый показатель – седнее квадратическое отклонение – представляет собой корень из дисперсии.

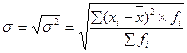
5-ый показатель. Коэффициент вариации – это отношение седнего квадратического отклонения к среднему значению.

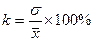
Коэффициент вариации применяется в следующих случаях:

- когда необходимо определить и сравнить степени рассеивания 2-х или нескольких признаков, выраженных в различных единицах измерения для характеристики одной и той же совокупности;

- когда необходимо определить рассеивание одного и того же признака в разных единицах совокупности, имеющих разные единицы измерений и разные ср. величины.

Если коэффициент вариации составляет более 0,40 то такая совокупность считается неоднородной.

Пример.

Имеются данные о стаже работы рабочих 3-х бригад:

I бригада – 15, 18, 20, 22, 25 лет;

II бригада – 10, 15, 20, 25, 30 лет;

III бригада – 8, 12, 17, 25, 38 лет.

Определить показатель вариации.

1. Размах вариации.

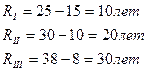
2. Среднее линейное отклонение.

I.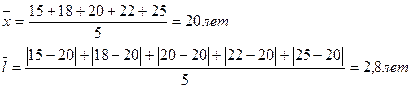

II.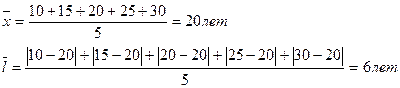

III.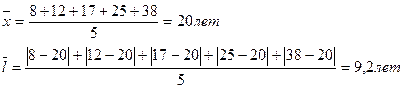

В I бригаде абсолютное отклонение каждого значения от средней величины 2,8 лет, во II бригаде – 6 лет, в III бригаде – 9,2 лет.

3. Дисперсия, средний квадрат отклонения.

I.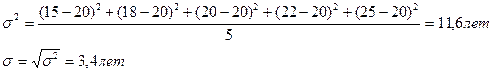

II.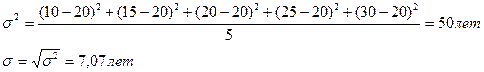

III.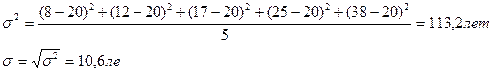

Чем больше ср. квадратическое отклонение, тем более высока вариация, т.е. более неточным будет среднее значение.

4. Коэффициент вариации.

I.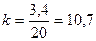

II.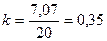

III.

III бригада является неоднородной совокупностью, т.к. коэффициент вариации составляет более 0,40.