Эксцентриситет алидады
В плоскости лимба горизонтального круга имеются три характерных точки:
D – центр круга делений лимба,
A – центр вращения алидады,
L – центр вращения лимба.
В идеальном теодолите все три точки должны совпадать, но в действительности они не совпадают. Несовпадение точки A с точкой D называется эксцентриситетом алидады, несовпадение точки L с точкой D называется эксцентриситетом лимба, несовпадение точек A и L называется эксцентриситетом осей.
Рассмотрим влияние эксцентриситета алидады на отсчеты по лимбу. Отрезок AD называется линейным элементом эксцентриситета алидады и обозначается буквой l.
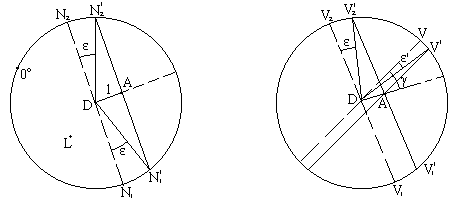
Некоторые теодолиты имеют два отсчетных устройства, отстоящих одно от другого на 180o. Вследствие эксцентриситета алидады отсчет по одному отсчетному индексу будет меньше правильного отсчета на угол ε:
N'1 = N1 – ε
по другому отсчетному индексу – больше правильного на угол ε:
N'2 = N2 + ε
Средний отсчет будет свободен от влияния эксцентриситета:
N = 0.5*(N1' + N2') = 0.5*(N1 + N2) .
Чтобы получить численное значение эксцентриситета, нужно из отсчета N2' вычесть отсчет N1':
N2' – N1' = N2 – N1 + 2*ε,
но N2 – N1 = 180o, поэтому:
ε = 0.5*(N'2 – N'1 + 180o).
При вращении алидады взаимное положение линейного элемента эксцентриситета алидады и отсчетных индексов изменяется, и величина ошибки отсчета ε' зависит от угла γ:
ε' = ε * sin(γ) .
У теодолитов с односторонним отсчитыванием отсчет по лимбу искажается на величину ε' с одним знаком при КЛ и с другим знаком при КП; в среднем отсчете влияние эксцентриситета исключается.
Из всех ошибок отсчитывания по лимбу, возникающих вследствие нарушения геометрических условий, можно выделить симметричные ошибки, то–есть такие, которые имеют разные знаки при КЛ и КП и влияние которых в среднем отсчете устраняется, и несимметричные ошибки, влияние которых в среднем отсчете не устраняется. К симметричным ошибкам относятся коллимационная ошибка, ошибка из–за неравенства подставок, ошибка эксцентриситета. К несимметричным ошибкам относятся ошибка наклона оси вращения алидады, ошибки делений лимба и некоторые другие.
Дата добавления: 2015-12-22; просмотров: 1479;
