Изокоста. Равновесие производителя.

Как и в теории потребительского выбора в теории производства также важно определить при каких условиях можно говорить о равновесии производителя. Для этого необходимо сопоставить производственную функция с затратами фирмы на производство, причем в разрезе затрат на различные факторы производства. Совокупные (общие) издержки в двухфакторной модели можно представить следующим уравнением:

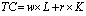
где ТС (total costs) – совокупные издержки,

w - ставка заработной платы (другой вариант написания - P_L),

r - цена (процент) использования капитала (другой вариант написания - P_K),

L, K - количество труда и капитала.

Информация об уровне издержек позволяет графически построить изокосту (линию равных затрат).

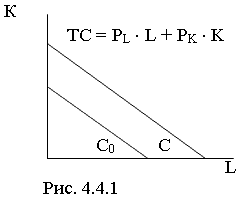
Изокоста включает в себя все возможные сочетания труда и капитала, которые имеют одну и ту же суммарную стоимость, то есть все сочетания факторов производства с равными валовыми издержками.

Изокоста графически представляет собой прямую линию, которая определяется двумя предельными точками – максимальным количеством труда и капитала, которое может приобрести фирма.

Изокоста имеет угловой коэффициент, равный отношению цен факторов производства, взятому с отрицательным знаком .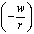

Это следует из уравнения изокосты: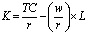

Используя изокосту, можно определить какой набор факторов производства обеспечивает заданный выпуск с наименьшими совокупными издержками (ТС). Решение данной проблемы – в точке касания (e) изокосты с изоквантой, которая отражает равновесие производителя.

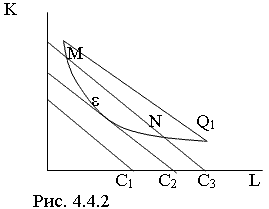
В точке e углы наклона изокванты и изокосты одинаковы, то есть:

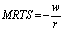
Выше было отмечено, что предельная норма технологического замещения соответствует углу наклона касательной к изокванте, а в ситуации равновесия изокоста является касательной, таким образом, ее угол наклона соответствует MRTS.

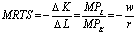
Наконец, из этого уравнения следует, что отношение предельного продукта каждого из факторов производства к их цене в точке e должны быть равны.

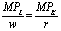
Это отношение отражает ситуацию равновесия производителя.