Поле преобразователя с акустической задержкой

Случай плоскопараллельной задержки.Данный тип задержки чаще всего реализуется при использовании иммерсионного метода. Распространение акустических волн в плоскопараллельной задержке представлено на рис. 2.13.

Упростить расчетную схему можно при использовании представления о мнимом преобразователе: действующий источник излучения 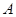заменяется мнимым источником 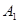(считается, что его лучи не преломляются на границе раздела сред).

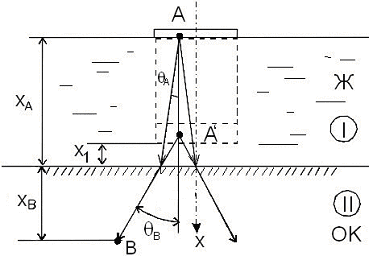
Рис. 2.13. Распространение акустических колебаний в плоскопараллельной задержке: Ж(I) – жидкость; ОК(II) – объект контроля; Х_А – путь ультразвука в жидкости ( в задержке); 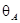–угол расхождения лучей в задержке; 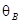– угол преломления лучей в объекте контроля; А – элементарный источник на кварцевой пластине; А¢ – мнимый источник; Х₁ – координаты мнимого источника

Тогда можно определить расстояние от поверхности изделия до мнимого излучателя следующим образом:

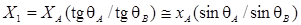. (2.27)

Есл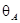и и 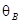– малы, то 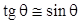. С учетом закона Снеллиуса можем произвести переход к соотношениям скоростей волн в контактирующих средах

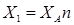, (2.28)

где 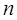– показатель преломления.

Таким образом, при малых значениях углов 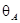и 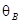величина 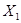не зависит от угла 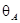. Если , то ошибка, связанная с заменой источника на мнимый, не превышает десяти процентов, что можно считать допустимым.

Таким образом, в расчетах возможна замена всех точек реальной пьезопластины на точки мнимого преобразователя. В этом случае уравнения акустического поля преобразователя должны быть заменены уравнениями, в которых ко всем значениям пути ультразвука в контролируемом объекте 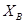нужно прибавить значение .

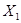Кроме того, необходимо учитывать акустические свойства реальной среды задержки. Все формулы для расчета поля ПЭП необходимо модифицировать следующим образом: в режиме излучения на границе между средой задержки и контролируемым объектом ввести коэффициент прозрачности по амплитуде ; при реализации режима излучения-приема необходимо вводить коэффициент преломления по интенсивности (энергии) ; учесть затухание, для чего в случае необходимости во все уравнения вводится дополнительный множитель 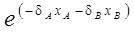; 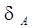учитывает расстояние до реального источника излучения. Если контролируется тонкостенное изделие, то можно не учитывать затухание в контролируемой среде .

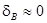Наклонная задержка.В случае наклонной задержки также возможно введение мнимого преобразователя. Точность при этом значительно ниже, чем в прямом преобразователе, также усложняется и схема расчета. Наклонный преобразователь с акустической задержкой (призмой) приведен на рис. 2.14. Считается, что излучатель уменьшается в некоторое число раз.

Введем следующие обозначения: – угол падения акустической оси; 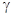– угол преломления акустической оси; 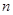– показатель преломления.

Размер мнимого преобразователя

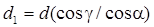. (2.29)

Расстояние до мнимого преобразователя

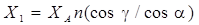. (2.30)

Поле в дальней зоне определяется формулой

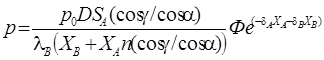, (2.31)

где 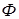– функция направленности поля, характеризующая мнимый источник.

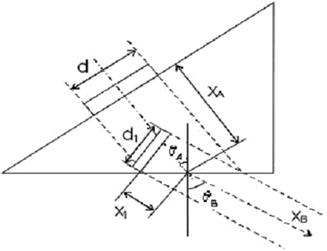
Рис. 2.14. Наклонная задержка: – диаметр преобразователя; 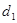– диаметр мнимого преобразователя; – средний путь в призме;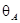–угол расхождения лучей в призме; 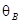– угол преломления лучей в изделии; 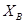– направление ультразвука в изделии; 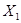– расстояние от поверхности изделия до мнимого излучателя.

Мнимый источник меньше действительного в 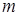раз:

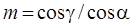. (2.32)

Акустическое поле в плоскости падения и в плоскости, перпендикулярной акустической оси, имеет разную структуру и различные амплитуду (в сечении для действительного источника поле представляет собой круг, для мнимого источника – овал).

Формула (2.31) дает достаточное совпадение с экспериментом, если угол падения попадает в интервал между первым и вторым критическим углом. В этом интервале изменение 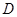невелико.

При использовании наклонного преобразователя наблюдаются три эффекта:

1.Вблизи критических углов наблюдается отклонение от закона Снеллиуса, при этом искажается поле в объекте контроля. В итоге максимум плотности излучения в объекте контроля и направление акустической оси не совпадают (рис. 2.15). Несовпадение акустической оси и центрального луча, соответствующего максимуму диаграммы направленности, объясняется тем, что при некоторых значениях угла падения , близких к критическим, коэффициент прозрачности 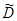быстро изменяется. При прохождении через границу раздела меньше ослабляются лучи диаграммы направленности, соответствующие большему значению 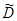. Отклонение экспериментального значения угла преломления (для центрального луча) от теоретического (рассчитанного по закону синусов) происходит в сторону углов, для которых значение 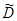больше. Углом ввода называют угол преломления центрального луча. Увеличение волнового размера пьезопластины (ak, где a – радиус пьезопластины) приводит к сужению диаграммы направленности в призме и ослаблению описанного эффекта. Увеличение угла призмы, в свою очередь, приводит к усилению данного эффекта.

2.В случае, когда боковые лепестки диаграммы направленности достаточно велики (рис. 2.17), возможно ухудшение чувствительности контроля за счет возникновения дополнительных шумов. Причиной их возникновения является отражение лучей боковых лепестков от различных препятствий в объекте контроля: дефектов, стенок, дна. Как следствие, возникают ложные сигналы, мешающие проведению контроля. Определить этот эффект можно с помощью демпфирования.

3.Чем больше угол ввода, тем сильнее будут сглаживаться осцилляции амплитуды в ближней зоне. Возникает деформация диаграммы направленности (рис. 2.16), эффект проявляется тем сильнее, чем меньше произведение аf, где f – частота, а – радиус пьезопластины.

При этом сильного влияния угла ввода на фронтальную разрешающую способность не наблюдается.

Если в общем случае диаграмма направленности узкая, то эффект деформации диаграммы будет слабо выражен. Для широких диаграмм этот эффект выражен более ярко.

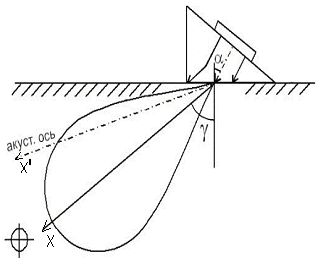
Рис. 2.15. Отклонение от закона Снеллиуса вблизи критического угла падения акустической оси: a – угол преломления лучей в призме; g – угол преломления лучей в среде; х – реальная ось ввода луча; х¢ – теоретическая ось ввода луча

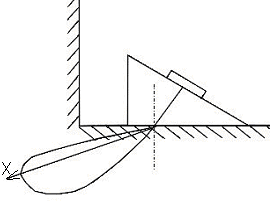
Рис. 2.16. Деформация диаграммы направленности: X – ось ввода луча

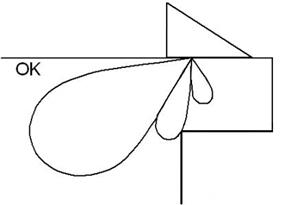
Рис. 2.17. Возникновение ложных сигналов при больших боковых лепестках диаграммы направленности наклонного преобразователя