Неопытные купальщики

Неопытные купальщики нередко подвергаются большой опасности только потому, что забывают об одном любопытном следствии закона преломления света: они не знают, что преломление словно поднимает все погруженные в воду предметы выше истинного их положения. Дно пруда, речки, каждого водоема представляется глазу приподнятым почти на третью часть глубины; полагаясь на эту обманчивую мелкость, люди нередко попадают в опасное положение. Особенно важно знать это детям и вообще людям невысокого роста, для которых ошибка в определении глубины может оказаться роковой.

Причина – преломление световых лучей. Тот же оптический закон, который придает полупогруженной в воду ложке изломанный вид (рис. 112), обусловливает и кажущееся поднятие дна. Вы можете проверить это.

Посадите товарища за стол так, чтобы он не мог видеть дна стоящей перед ним чашки. На дно ее положите монету, которая, разумеется, будет заслонена стенкой чашки от глаз вашего товарища. Теперь попросите товарища не поворачивать головы и налейте в чашку воды. Произойдет нечто неожиданное: монета сделается для вашего гостя видимой! Удалите воду из чашки спринцовкой, – и дно с монетой опять опустится (рис. 113).

Рис. 114 объясняет, как это происходит. Участок дна m кажется наблюдателю (глаз которого – над водой, в точке A) в приподнятом положении: лучи преломляются и, переходя из воды в воздух, вступают в глаз, как показано на рисунке, а глаз видит участок на продолжении этих линий, т. е. над m. Чем наклоннее идут лучи, тем выше поднимается m. Вот почему при рассматривании, например, с лодки ровного дна пруда нам всегда кажется, что оно наиболее глубоко прямо под нами, а кругом – всё мельче и мельче.

Итак, дно пруда кажется нам вогнутым. Наоборот, если бы мы могли со дна пруда смотреть на перекинутый через него мост, он казался бы нам выпуклым (как изображено на рис. 115; о способе получения этой фотографии будет сказано позже). В данном случае лучи переходят из слабо преломляющей среды (воздуха) в сильно преломляющую (воду), поэтому и эффект получается обратный, чем при переходе лучей из воды в воздух. По сходной причине и ряд людей, стоящих, например, возле аквариума, должен казаться рыбам не прямой шеренгой, а дугой, обращенной своей выпуклостью к рыбе. О том, как видят рыбы, или, вернее, как они должны были бы видеть, если бы имели человеческие глаза, мы скоро побеседуем подробнее.

Рисунок 112. Искаженное изображение ложки, опущенной в стакан с водой.

Рисунок 113. Опыт с монетой в чашке.

Рисунок 114. Почему монета в опыте рис 113 кажется приподнявшейся.

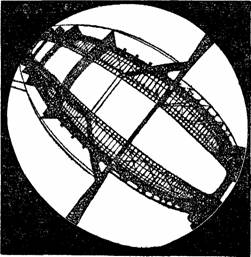
Рисунок 115. В таком виде представляется подводному наблюдателю железнодорожный мост, перекинутый через pекy (с фотографии проф. Вуда).

Невидимая булавка

Воткните булавку в плоский пробковый кружок и положите его булавкой вниз на поверхность воды в миске. Если пробка не чересчур широка, то, как бы ни наклоняли вы голову, вам не удастся увидеть булавки – хотя казалось бы, она достаточно длинна, чтобы пробка не заслоняла ее от вас (рис. 116).

Почему же лучи света не доходят от булавки до вашего глаза? Потому что они претерпевают то, что в физике называется «полным внутренним отражением». Напомним, в чем состоит это явление. На рис. 117 можно проследить за путями лучей, переходящих из воды в воздух (вообще из среды более преломляющей в среду менее преломляющую) и обратно. Когда лучи идут из воздуха в воду, то они приближаются к «перпендикуляру падения»; например, луч, падающий на воду под углом b к перпендикуляру к плоскости падения, вступает в нее уже под углом a, который меньше, чем b.

Но что бывает, когда падающий луч, скользя по поверхности воды, падает на водную поверхность почти под прямым углом к перпендикуляру? Он вступает в воду под углом, меньшим чем прямой, а именно под углом всего в 48,5 градусов. Под большим углом к перпендикуляру, чем 48,5 градусов, луч вступить в воду не может; это для воды «предельный» угол. Необходимо уяснить себе эти несложные соотношения, чтобы понять дальнейшие, совершенно неожиданные и чрезвычайно любопытные следствия закона преломления.

Рисунок 116. Опыт с булавкой, невидимой в воде.

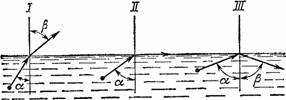
Рисунок 117. Разные случаи преломления луча при переходе из воды в воздух. В случае II луч падает под предельным углом к перпендикуляру падения и выходит из воды, скользя вдоль ее поверхности. III изображает случай полного внутреннего отражения.

Мы сейчас узнали, что лучи, падающие на воду под всовозможными углами, сжимаются под водой в довольно тесный конус с углом раствора 48,5 + 48,5 = 97°. Проследим теперь за ходом лучей, идущих обратно – из воды в воздух (рис. 118). По законам оптики, пути будут те же самые, и все лучи, заключенные в упомянутом 97‑градусном конусе, выйдут в воздух под различными углами, распределяясь по всему 180‑градусному пространству над водой.

Но куда же денется подводный луч, находящийся вне упомянутого конуса? Оказывается, он не выйдет вовсе из‑под воды, а отразится целиком от ее поверхности, как от зеркала. Вообще всякий подводный луч, встречающий поверхность воды под углом, большим «предельного» (т. е. большим 48,5 градусов), не преломляется, а отражается: он претерпевает, как говорят физики, «полное внутреннее отражение[61]».

Если бы рыбы изучали физику, то главнейшим отделом оптики было бы для них учение о «внутреннем отражении», так как в их подводном зрении оно играет первостепенную роль.

В связи с особенностями подводного зрения находится, по всей вероятности, то обстоятельство, что многие рыбы имеют серебристую окраску. По мнению зоологов, такая окраска есть результат приспособления рыб к цвету расстилающейся над ними водной поверхности: при наблюдении снизу поверхность воды, как мы знаем, кажется зеркальной – вследствие «полного внутреннего отражения»; а на таком фоне серебристо‑окрашенные рыбы остаются незаметными для охотящихся на них водных хищников.

Рисунок 118. Лучи, исходящие из точки P под углом к перпендикуляру падения больше предельного (для воды – 48,5 градусов), не выходят в воздух из воды, а целиком отражаются внутрь.

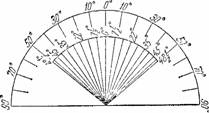
Рисунок 119. Дуга наружного мира в 180° сокращается для подводного наблюдателя до дуги в 97°; сокращение тем сильнее, чем далее отстоит часть дуги от точки зенита (0°).