Исследовательский этап
Цели: 1) выявить решения, отвечающие выбранному критерию;
2) определить возможности реализации предложенных решений.
4.1. экспертиза подготовленных решений;
4.2. отбор наиболее рациональных вариантов решений;
4.3. проведение испытаний;
4.4. технико-экономическое обоснование решений.
Рекомендательный этап
Необходимо обсудить предложения по совершенствованию объектов ФСА, утвердить план мероприятий по внедрению.
Внедрение
Вывод: ФСА — довольно сложный процесс, нововведение. В отличие от предметного подхода (в т.ч. бухгалтерского учета), ФСА предполагает использование и таких неопределенных факторов как субъективное восприятие и понимание проблемы.
ФСА — это новый шаг в экономике — анализ полезности вещи. Т. е. он изучает вещь, новые услуги, идеи с точки зрения ее функциональности, где вся вещь разбивается на много функций, которые она в себе несет. Эти функции могут быть полезными и бесполезными, и даже вредными. Искусство ФСА состоит в том, чтобы разделить эти функции одну от другой, уметь их систематизировать и изучать уже как единственную, также и во взаимосвязи с соседними функциями, и как на изменение одной из них отреагирует система в целом. Зная каждые функции можно, в пределах возможного поменять одну, полезную, или убрать вредную. Все это в совокупности направлено как на потребителя, с точки зрения понижения цены, так и на производителя, с точки зрения понижения себестоимости, а значит и увеличения объема выпуска.
Тема 4: «Принятие решений в различных условиях»
1. Принятие решений в условиях риска.
- Риск вложения в ценные бумаги. Виды риска.
- Учет риска инвестирования
2. Принятие решений в условиях неопределенности.
- критерии Вальда, Сэвиджа, Гурвица.
В зависимости от хар-ра внешней среды выделяются следующие условия, в которых принимаются решения:
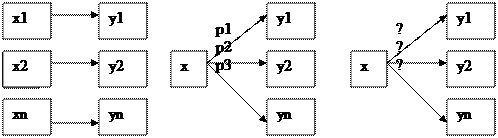
1. Принятие решений в условиях определенности - когда каждому решению xЄХ => соответствует определенный результат уЄУ. xày1, x2ày2, xnàyn
2. Принятие решений в условиях риска - каждому решению соответствует не 1, а множество результатов, с определенной вероятностью (Р). xàp1ày1, xàp2ày2, xàp3ày3. где Р- выполняемость.
3. Принятие решений в условиях неопределенности – когда каждому решению соответствует множество результатов, но вероятности появления этих результатов неизвестны.
4. условие активной внешней среды каждому решению (Х) соответствует результат (У), который является функцией от действия активной внешней среды; xày=f (активн внеш среда)
5. конфликтная - - когда интересы противоположны;
 |
1. Принятие решений в условиях риска
Принятие решений в условиях риска - каждому решению соответствует не 1, а множество результатов, с определенной вероятностью. Вер-ть опр-ся на основе стат данных, а при их отсутствии – на основе экспертных оценок. Кроме вероятности, существуют следующие характеристики события: дисперсия, математическое ожидание, мода, медиана.
Принятие решений в условиях риска д.б. основано на теории предельной полезности. Суть ее – приобретение дополнительного результата сравнивается с фактическим результатом, который человек имеет гарантировано.
Пример: Наниматель предлагает работнику оплатить результат на выбор
1)Просто заплатить за работу 100 руб.,
2)Бросить жребий и заплатить 150 руб. или 50 руб.
Какой вариант лучше выбрать?
∑PiХi=0,5*150+0,5*50=100. Нет смысла!
Если бы предложили 160 и 50: 0,5*160+0,5*50=105,
180 и 50: 90+25=115,
200 и 50: 100+25=125.
Т.е. если предельная полезность возрастет, то есть смысл.
Функционирование и развитие п/п, как правило, связано с элементами неопределенности, т.е. часто возникают ситуации, не имеющие однозначного исхода (решения).
Поэтому необходимо использовать методов, которые дают возможность по заданным целям и ограничениям получить приемлемые для практики (оптимальные или рациональные) управленческие решения.
В общем виде постановка и решение задачи оптимизации решений, принимаемых в условиях риска, может быть представлена следующим образом:
· имеется m возможных решений Р1,Р2,…, Рm;
· условия обстановки точно неизвестны, но о них можно сделать n предположений О1, О2,…, On;
· каждой паре сочетаний решений Р и обстановки Осоответствует определенный результат, так называемый выигрыш аij – показатель эффективности решений, к-ый может быть представлен в виде таблицы эффективности или выигрышей, т.н. платежная матрица (табл. 4.2) Т.о. выигрыш хар-ет определенную величину рез-та (доход, прибыль и т.д.).
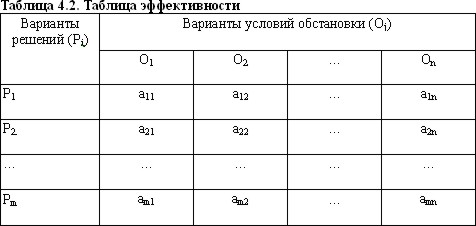
Т.о., выбор решения в условиях риска предполагает, что вероятности возможных вариантов обстановки известны. Эти вероятности определяются на основе статистических данных, а при их отсутствии — на основе экспертных оценок. Результаты принятых решений существенно зависят от обстановки, которая в значительной мере неопределенна.
Рассмотрим следующую задачу.
Предприятие готовится к переходу на новые виды продукции, при этом возможны четыре решения Р1 , Р2 , Р3, Р4 каждому из которых соответствует определенный вид выпуска или их сочетание.
Результаты принятых решений существенно зависят от обстановки, которая в значительной мере неопределенна. Варианты обстановки характеризует структура спроса на новую продукцию, которая м б трех типов: О1,О2, О3.
Необходимо найти такую стратегию (линию поведения) — решение Р, которая по сравнению с другими является наиболее выгодной (целесообразной).
Выигрыш, характеризующий относительную величину результата (доходы, прибыль и т.п.), соответствующий каждой паре сочетаний решений Р и обстановки О, представлен в табл. 4.3.
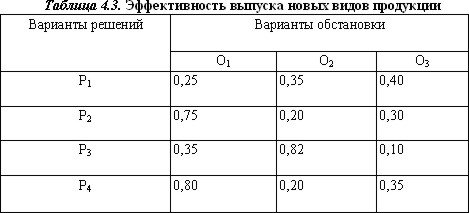
При обстановке О3 решение Р2 в три раза лучше, чем Р3, а решение Р1 неодинаково для обстановки О1 и О3 и т.д.
Например, если точно известно, что наступит обстановка О1, следует принимать решение Р4, которое в данной обстановке обеспечит наибольший выигрыш — 0,80.
Если мы приняли решение Р3 (в надежде на обстановку О2), а наступила обстановка О1,то мы получаем выигрыш, равный 0,35 (вместо 0,82 при принятии решения Р4). Таким образом, потери при принятии решения Р3 и наступлении обстановки О1, (Н31) составляют 0,82-0,35=0,47.
Наличие выигрышей позволяет определить потери в результате принятия неоптимальных решений — в случае, когда ожидаемое условие обстановки (имеющее вероятностный характер) не произошло.
Применяется специальный показатель - показатель потерь, который свидетельствует, насколько выгодна применяемая нами стратегия в данной конкретной обстановке с учетом степени ее неопределенности.
В общем случае потери Нij, соответствующие каждой паре сочетаний решений Рi и обстановки Qj, определяются как разность между максимальным выигрышем и выигрышем по конкретному решению при данной обстановке.
Полученные таким образом потери для всех решений при всех вариантах обстановки представлены в табл. 4.4.
|
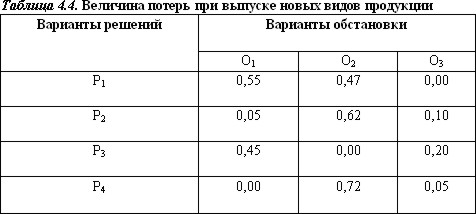
Приведенная таблица потерь существенно дополняет таблицу эффективности.
Так, основываясь на таблице эффективности, можно прийти к выводу, что решение Р1 при обстановке О2 равноценно решению Р4 при обстановке О3. Однако анализ указанных решений с использованием данных таблицы 4.4 показывает, что они составляют соответственно 0,47 и 0,05.
Такая существенная разница объясняется тем, что способ решения Р1 при обстановке О2 имеет эффективность 0,35, в то время как при этой же обстановке можно получить эффективность до 0,82.
При выборе решения используется критерий риска или вероятность возникновения потерь.
Предпочтение отдается решению, имеющему наименьший средневзвешенный показатель риска. Он определяется как сумма произведений вероятностей различных вариантов обстановки на соответствующее им значение потерь
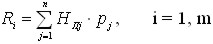
Так, пусть вероятность первого варианта обстановки О1= 0,5, второго — 0,3 и третьего — 0,2, тогда показатель риска R для каждого из решений составит:
R1 = 0,55 • 0,5 + 0,47 • 0,30 + 0,00 • 0,2 = 0,416
R2= 0,05 • 0,5 + 0,62 • 0,3 + 0,10 • 0,2 = 0,231
R3 = 0,45 • 0,5 + 0,00 • 0,3 + 0,30 • 0,2 = 0,285
R4 = 0,00 • 0,5 + 0,72 • 0,3 + 0,05 • 0,2 = 0,226 = min
Следовательно, решение Р4 для данных условий является наименее рискованным.
Такой подход к принятию решений в условиях риска позволяет получить лишь вероятностные (средневзвешенные) результаты анализа возможных вариантов. Но использование рассмотренного метода значительно повышает степень достоверности оценок и результатов по сравнению с подходами к принятию решений без количественной оценки вариантов.
3. Принятие решений в условиях неопределенности
Игры с природой (статистические игры). Когда 2-я сторона (природа) – пассивна, не противодействует. Для того, чтобы выбрать решение строится платежная матрица.
ПРИМЕР: С/х п/п имеет 3 участка земли А1-повышенной влажности, А2-средней влажности, А3-сухой. Погодные условия П1-осадков меньше нормы, П2-норма, П3-осадков больше нормы.
Платежная матрица представляет собой среднюю урожайность на каждом участке в зависимости от погодных условий.
| П1 | П2 | П3 | |
| А1 | |||
| А2 | |||
| А3 |
Возможны 2 вида стратегии:
1)Смешанная (часть там, часть тут);
2)Чистая (только здесь или только там).
Наша задача – выбрать чистую стратегию.
Критерии выбора решений:
При принятии решений в условиях неопределенности, когда вероятности возможных вариантов обстановки неизвестны, могут быть использованы критерии, выбор которых зависит также от склонности к риску лиц, принимающих решения.
К числу классических критериев, которые используются при принятии решений в условиях неопределенности, можно отнести:
- максиминный критерий Вальда (крайнего пессимизма);
- минимаксный критерий Сэвиджа (минимального риска);
- критерий обобщенного максимина (пессимизма-оптимизма) Гурвица.
Максиминный критерий Вальда используется в случаях, когда требуется гарантия, чтобы выигрыш в любых условиях оказывался не менее, чем наибольший из возможных в худших условиях, т.е. обеспечивается успех при любых возможных условиях.
Наилучшим решением будет то, для которого выигрыш окажется максимальным из всех минимальных при различных вариантах условий.
Формализованное выражение критерий максимина: 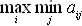
Исходными данными при выборе вариантов решений по критерию Вальда являются выигрыши аij, соответствующие каждой паре сочетаний решений Р и обстановки О (матрица эффективности решений)
Максимальный из минимальных результатов равен 0,25 и, следовательно, предпочтение необходимо отдать варианту Р1 обеспечивающему этот результат.
Это максимальный гарантированный результат (выигрыш), который может быть получен в условиях имеющихся исходных данных. Выбрав решение Р1 мы независимо от вариантов обстановки получим выигрыш не менее 0,25. При любом другом решении, в случае неблагоприятной обстановки, может быть получен результат (выигрыш) меньше 0,25.
Данный критерий прост и четок, но консервативен в том смысле, что ориентирует принимающего решение на слишком осторожную линию поведения.
Этот критерий никак не учитывает, что в случае принятия решения Р1, (т.е. при ориентации на выигрыш 0,25), максимальный выигрыш не превышает 0,4. В то время как выбирая, например, решение Р4, при гарантированном выигрыше 0,20 в случае благоприятной обстановки можно получить выигрыш, равный 0,80.


Минимаксный критерий Сэвиджа используется в тех случаях, когда требуется в любых условиях избежать большого риска.
В соответствии с этим критерием предпочтение следует отдать решению, для которого потери максимальные при различных вариантах условий окажутся минимальными.Его формализованное выражение
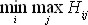
где Нij, — потери, соответствующие i-му решению при j-м варианте обстановки.


Этот критерий также относится к разряду осторожных. Однако, в отличие от критерия Вальда, который направлен на получение гарантированного выигрыша, критерий Сэвиджа минимизирует возможные потери.
Здесь в качестве исходных данных при выборе решений выступают потери (Нij), соответствующие каждой паре сочетаний решений Р и обстановки О.
Минимальные из максимальных потерь составляют 0,45 и, следовательно, предпочтение необходимо отдать варианту Р3 обеспечивающему эти потери.
Основным исходным допущением этого критерия является предположение о том, что на наступление вариантов обстановки оказывают влияние действия разумных противников (конкурентов), интересы которых прямо противоположны интересам лица, принимающего решение. Поэтому, если у противников (конкурентов) имеется возможность извлечь какие-либо преимущества, то они это обязательно сделают. Это обстоятельство заставляет лицо, принимающее решение, обеспечить минимизацию потерь вследствие этих действий.
Критерий обобщенного максимина (пессимизма — оптимизма) Гурвица используется, если требуется остановиться между линией поведения в расчете на худшее и линией поведения в расчете на лучшее.
В этом случае предпочтение отдается варианту решений, для которого окажется максимальным показатель G, определяемый из выражения:
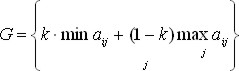 max
max 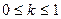
аij — выигрыш, соответствующий i-му решению при j-м варианте обстановки.
k — коэфф-т, рассматриваемый как показатель оптимизма (0  k
k  1),
1),
при к = 1 — в расчете на худшее; (критерий Гурвица совпадает с критерием Вальда, т.е. ориентация на осторожное поведение).
при k = 0 — линия поведения в расчете на лучшее, ориентация на предельный риск, т.к. большой выигрыш, как правило, сопряжен с большим риском. (0 – оптимизм) ------> (1 – пессимизм)
k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от конкретной обстановки и склонности к риску лица, принимающего решение.
Значения показателя G для различных вариантов решений в зависимостиот величины коэффициента k.
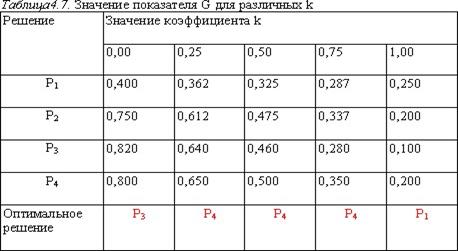
Т.о., с изменением коэффициента k изменяется вариант решения, которому следует отдать предпочтение.
Нами рассмотрены наиболее общие (классические) методы, которые позволяют обосновывать и принимать решение при неопределенности экономических данных и ситуаций, недостатке фактической информации об окружающей среде и перспективных ее изменений.
Дата добавления: 2015-12-08; просмотров: 1891;
