Характеристики направленности плоского излучающего раскрыва
Рассмотрим вопрос о КНД апертурных антенн. С этой целью воспользуемся еще одним определением КНД, определяющим данный параметр как отношение квадратов напряженности полей (плотностей потока мощности), создаваемых в точке приема направленной (в направлении максимума) и ненаправленной антеннами при одинаковых мощностях излучения:
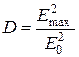 . (7.6)
. (7.6)
Для ненаправленной антенны имеем
 . (7.7)
. (7.7)
Мощность излучения апертурной антенны можно определить как мощность, проходящую через площадь раскрыва антенны
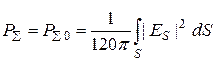 , (7.8)
, (7.8)
где 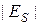 – действующее значение касательной составляющей напряженности электрического поля на элементе
– действующее значение касательной составляющей напряженности электрического поля на элементе 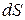 в плоскости раскрыва.
в плоскости раскрыва.
Подставляя (7.8) в (7.7), получаем
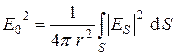 . (7.9)
. (7.9)
Действующее значение напряженности поля в направлении максимума излучения направленной антенны, т.е. вдоль оси z равно
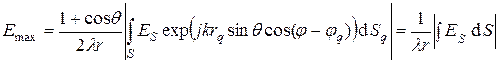 . (7.10)
. (7.10)
Подставляя (7.9) и (7.13) в (7.6), получаем
 , (7.11)
, (7.11)
где 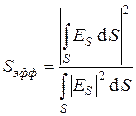 . (7.12)
. (7.12)
Эффективная поверхность плоских раскрывов целиком определяется их геометрическими размерами, формой и законами распределения поля в пределах этих площадок. В частности, если  , т.е. в пределах апертуры постоянна, то
, т.е. в пределах апертуры постоянна, то
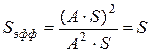 . (7.13)
. (7.13)
Таким образом, для равномерно и синфазно возбужденных апертур (в том числе прямоугольной и круглой)
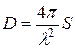 . (7.14а)
. (7.14а)
Для прямоугольного раскрыва выражение (7.14а) сводится к виду:
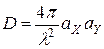 . (7.14б)
. (7.14б)
В остальных случаях
 , (7.15)
, (7.15)
где  – апертурный коэффициент использования площади раскрыва (
– апертурный коэффициент использования площади раскрыва ( 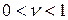 ). Очевидно, что для равномерно и синфазно возбужденных апертур
). Очевидно, что для равномерно и синфазно возбужденных апертур 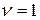 .
.
Рупорные антенны.
Наиболее простым типом рупорных антенн является открытый конец волновода. Он обладает слабой направленностью (т. к. его размер меньше  ) и плохо согласован со свободным пространством. Плавное увеличение размеров волновода, превращающее его в рупор, позволяет устранить эти недостатки. В горле рупора, т. е. в месте соединения его с волноводом, все же возникают высшие типы волн. Однако, если угол раскрыва рупора не очень велик, то волны высших типов быстро затухают, и в рупоре распространяется только волна основного типа.
) и плохо согласован со свободным пространством. Плавное увеличение размеров волновода, превращающее его в рупор, позволяет устранить эти недостатки. В горле рупора, т. е. в месте соединения его с волноводом, все же возникают высшие типы волн. Однако, если угол раскрыва рупора не очень велик, то волны высших типов быстро затухают, и в рупоре распространяется только волна основного типа.
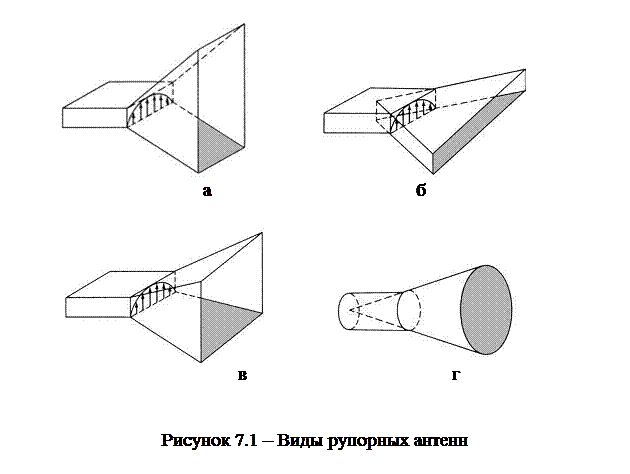
Основные типы рупоров образуются в результате расширения круглого или прямоугольного волновода. При расширении волновода в одной плоскости образуется секториальныйрупор (рисунок 7.1,а,б): H–плоскостный (рисунок 7.1,а), если расширяется плоскость вектора H, и E–плоскостный (рисунок 7.1,б), если расширяется плоскость вектора E. В первых силовые линии электрического поля перпендикулярны широкой стороне раскрыва, а во-вторых – узкой.
ри расширении волновода сразу в двух плоскостях образуется пирамидальный рупор (рисунок 7.1,в). Расширяющийся круглый волновод образует конический рупор (рисунок 7.1,г).
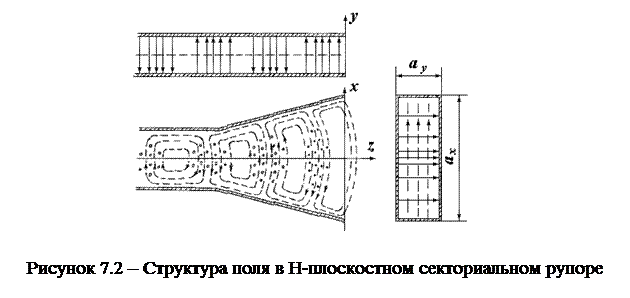
 Структура поля в рупоре в основном сохраняется той же, что и в волноводе. Для примера на рисунке 7.2 показана структура поля в H–плоскостном секториальном рупоре. Фронт волны из плоского (в волноводе) преобразуется в цилиндрический. Амплитудное распределение поля вдоль цилиндрической поверхности фронта волны полностью совпадает с амплитудным распределением в поперечном сечении волновода. Фазовая скорость распространения волны в каждом сечении рупора равна скорости волны в волноводе с тем же сечением и убывает от значения фазовой скорости волны в волноводе до скорости света у раскрыва рупора.
Структура поля в рупоре в основном сохраняется той же, что и в волноводе. Для примера на рисунке 7.2 показана структура поля в H–плоскостном секториальном рупоре. Фронт волны из плоского (в волноводе) преобразуется в цилиндрический. Амплитудное распределение поля вдоль цилиндрической поверхности фронта волны полностью совпадает с амплитудным распределением в поперечном сечении волновода. Фазовая скорость распространения волны в каждом сечении рупора равна скорости волны в волноводе с тем же сечением и убывает от значения фазовой скорости волны в волноводе до скорости света у раскрыва рупора.
Поскольку фазовый фронт волны в рупоре цилиндрический, а геометрический раскрыв плоский, поле в раскрыве оказывается несинфазным. Определим фазовые искажения.
Линией равных фаз в рупоре является дуга окружности с центром в точке O (рисунок 7.3). Фаза поля в произвольной точке  отстает от фазы поля в середине раскрыва (точка
отстает от фазы поля в середине раскрыва (точка 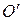 ) на величину
) на величину
 (7.16)
(7.16)
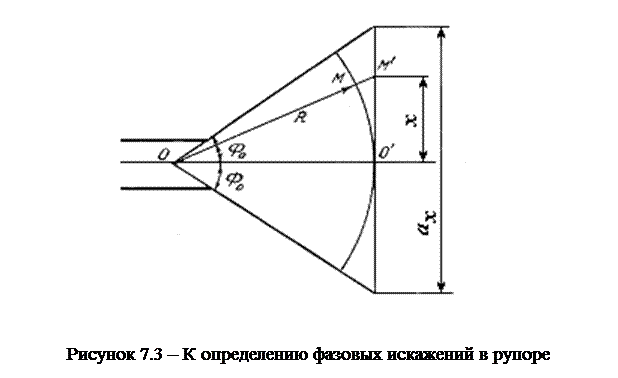 Как следует из рисунка 7.3, через
Как следует из рисунка 7.3, через 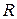 обозначена длина рупора, а через
обозначена длина рупора, а через 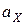 и
и 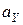 – размеры его раскрыва в плоскостях H и E соответственно. Так как в рупорах обычно выполняются соотношения
– размеры его раскрыва в плоскостях H и E соответственно. Так как в рупорах обычно выполняются соотношения 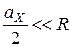 ,
, 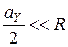 , то
, то
 , (7.17)
, (7.17)
т.е.  . (7.18)
. (7.18)
Таким образом, фаза поля в раскрыве рупора убывает к краям раскрыва приблизительно по квадратичному закону. Максимальный сдвиг фаз составляет величину
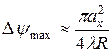 . (7.19)
. (7.19)
Формулы (7.18) и (7.19) справедливы при 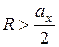 или
или 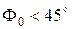 (
( 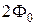 –угол раскрыва рупора). Обычно в рупорах, применяемых на практике, данные условия выполняются.
–угол раскрыва рупора). Обычно в рупорах, применяемых на практике, данные условия выполняются.
КНД рупорной антенны сложным образом зависит от ее размеров. Для каждой длины рупора 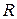 существует определенная ширина раскрыва
существует определенная ширина раскрыва 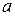 , при которой КНД достигает максимального значения. Дальнейшее увеличение
, при которой КНД достигает максимального значения. Дальнейшее увеличение 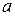 при фиксированной длине
при фиксированной длине 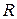 приводит к резкому росту фазовых искажений. Рупор, который при заданной длине имеет максимальный КНД и минимальную ширину луча, называется оптимальным.
приводит к резкому росту фазовых искажений. Рупор, который при заданной длине имеет максимальный КНД и минимальную ширину луча, называется оптимальным.
Максимальная несинфазность на краю раскрыва несинфазного H–плоскостного рупора составляет величину 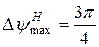 . С учетом этого из (7.19) можно получить
. С учетом этого из (7.19) можно получить
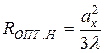 . (7.20)
. (7.20)
Коэффициент использования площади раскрыва H–плоскостного оптимального рупора составляет 0.64, а ширина луча определяется соотношением
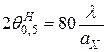 град. (7.21)
град. (7.21)
Для оптимального E–плоскостного секториального рупора максимальная несинфазность на краю раскрыва составляет 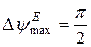 , чему соответствует
, чему соответствует
 . (7.22)
. (7.22)
КИП раскрыва такого рупора также равен 0.64, а ширина луча определяется соотношением
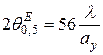 град. (7.23)
град. (7.23)
То обстоятельство, что в оптимальном H–плоскостном секториальном рупоре допускается более значительная несинфазность на краю раскрыва, чем в оптимальном E–плоскостном секториальном рупоре, обусловлено спаданием в H–плоскости амплитудного распределения на краях раскрыва до нуля, что уменьшает вес, с которым ошибка влияет на ДН.
Пирамидальный рупор можно рассматривать как сочетание E– и H–плоскостных секториальных рупоров. Фронт волны в пирамидальном рупоре приближенно можно считать сферическим. Структура поля в плоскостях E и H подобна структуре полей соответствующих секториальных рупоров. Если размеры раскрыва пирамидального рупора больше 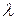 , то распределение поля в раскрыве можно считать разделяющимся (по координатам
, то распределение поля в раскрыве можно считать разделяющимся (по координатам 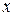 и
и 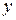 ). При этом ДН в двух главных плоскостях зависят только от размеров раскрыва в соответствующих плоскостях. КИП оптимального пирамидального рупора
). При этом ДН в двух главных плоскостях зависят только от размеров раскрыва в соответствующих плоскостях. КИП оптимального пирамидального рупора 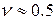 .
.
Фазовые искажения в рупорах могут быть уменьшены путем применения корректирующих линз, в качестве которых могут использоваться замедляющие диэлектрические линзы или ускоряющие металлопластинчатые линзы.
Зеркальные антенны
Зеркальными называются антенны, у которых поле в раскрыве формируется за счет отражения электромагнитной волны, созданной первичным источником, от металлической поверхности специального рефлектора (зеркала). Первичный источник электромагнитной волны называется в этом случае облучателем.
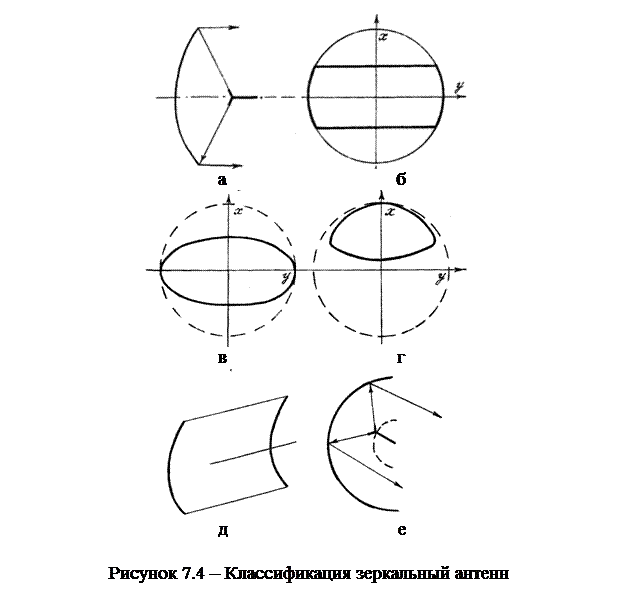 Существует много разновидностей зеркальных антенн. Их можно классифицировать по количеству зеркал и по геометрии отражающей поверхности. По геометрии отражающей поверхности зеркальные антенны можно разделить на параболоиды вращения (рисунок 7.4,а), симметричные (рисунок 7.4,б,в) и несимметричные (рисунок 7.4,г) вырезки из них, параболические цилиндры (рисунок 7.4,д) и сферические зеркала (рисунок 7.4,е).
Существует много разновидностей зеркальных антенн. Их можно классифицировать по количеству зеркал и по геометрии отражающей поверхности. По геометрии отражающей поверхности зеркальные антенны можно разделить на параболоиды вращения (рисунок 7.4,а), симметричные (рисунок 7.4,б,в) и несимметричные (рисунок 7.4,г) вырезки из них, параболические цилиндры (рисунок 7.4,д) и сферические зеркала (рисунок 7.4,е).
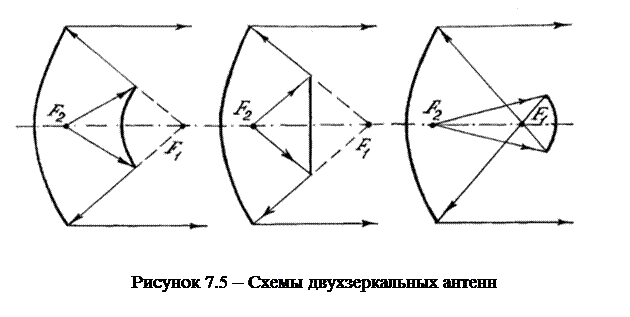 Помимо рассмотренных выше однозеркальных антенн, широкое распространение на практике получили двухзеркальные антенны. В этих антеннах для получения синфазного распределения поля в раскрыве используется две отражающие поверхности. Одна из них (большая) является основным зеркалом, которое чаще всего выполняется как параболоид вращения. Вторая (меньшая) может быть гиперболоидом (в частном случае плоскостью) или эллипсоидом. В первом случае (рисунок 7.5,а,б) антенну называют антенной Кассегрена, во втором (рисунок 7.5,в) – антенной Грегори. Эти названия, как и сами схемы антенн, заимствованы из оптики.
Помимо рассмотренных выше однозеркальных антенн, широкое распространение на практике получили двухзеркальные антенны. В этих антеннах для получения синфазного распределения поля в раскрыве используется две отражающие поверхности. Одна из них (большая) является основным зеркалом, которое чаще всего выполняется как параболоид вращения. Вторая (меньшая) может быть гиперболоидом (в частном случае плоскостью) или эллипсоидом. В первом случае (рисунок 7.5,а,б) антенну называют антенной Кассегрена, во втором (рисунок 7.5,в) – антенной Грегори. Эти названия, как и сами схемы антенн, заимствованы из оптики.
В антенне Кассегрена малое зеркало располагают так, чтобы один из фокусов гиперболы совпал с фокусом параболы 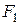 . Во втором фокусе гиперболы (
. Во втором фокусе гиперболы ( 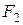 ) помещают облучатель. Исходящие из второго фокуса лучи после отражения от малого зеркала принимают такие направления, как будто они исходят из первого фокуса. Особенно наглядно это видно в случае плоского вспомогательного зеркала (рисунок 7.5,б).
) помещают облучатель. Исходящие из второго фокуса лучи после отражения от малого зеркала принимают такие направления, как будто они исходят из первого фокуса. Особенно наглядно это видно в случае плоского вспомогательного зеркала (рисунок 7.5,б).
В антенне Грегори с фокусом 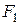 параболы совмещают один из фокусов эллипса. Во втором фокусе эллипса также помещают облучатель. Излученная волна после отражения от малого зеркала фокусируется в точке
параболы совмещают один из фокусов эллипса. Во втором фокусе эллипса также помещают облучатель. Излученная волна после отражения от малого зеркала фокусируется в точке 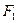 , которая играет роль фиктивного облучателя параболы.
, которая играет роль фиктивного облучателя параболы.
 В схеме Кассегрена малое зеркало помещают между параболой и ее фокусом, в то время как в схеме Грегори – за фокусом параболы. В связи с этим габаритный размер схемы Грегори больше и она используется реже.
В схеме Кассегрена малое зеркало помещают между параболой и ее фокусом, в то время как в схеме Грегори – за фокусом параболы. В связи с этим габаритный размер схемы Грегори больше и она используется реже.
Одно из основных преимуществ двухзеркальных антенн перед однозеркальными состоит в том, что наличие двух отражающих поверхностей предоставляет дополнительную степень свободы, которая может быть использована для регулировки амплитудного распределения в раскрыве, уменьшения фазовых ошибок при качании луча и т. п. В связи с этим КИП двухзеркальных антенн выше, чем у однозеркальных, и достигает 0.6–0.65.
Другое преимущество заключается в том, что облучатель может быть размещен вблизи вершины большого зеркала, за которым находятся передатчик и элементы фидерного тракта. При этом существенно сокращается длина волновода, идущего к облучателю. Это упрощает конструкцию фидерного тракта, улучшает согласование, уменьшает потери и шумовую температуру антенно-фидерного устройства.
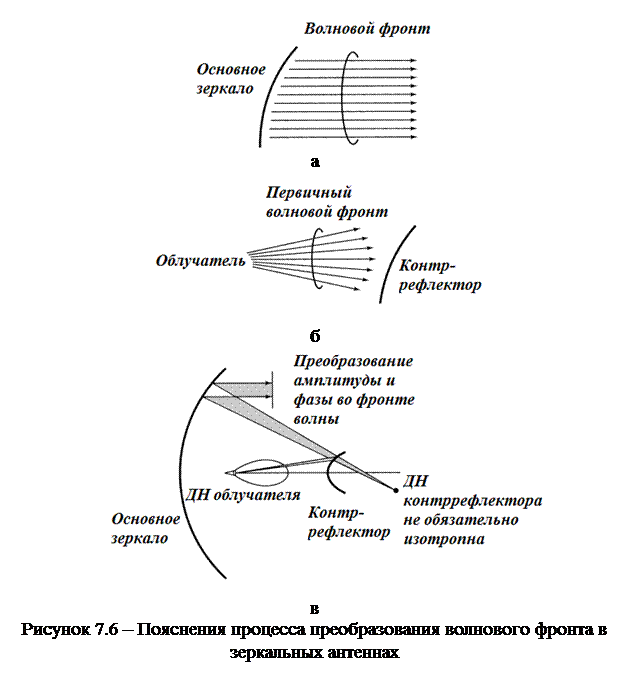
Основная задача антенны – трансформировать сферическое поле облучателя в поле плоской волны. На рисунке 7.6 даны пояснения процесса преобразования волнового фронта в зеркальных антеннах. Здесь на рисунке 7.6,а показано преобразование волнового фронта при использовании одного зеркала, а на рисунке 7.6,б – двух зеркал. Рисунок 7.6,в поясняет трансформацию волнового поля в двухзеркальной антенне.
 Профиль отражающего зеркала можно определить, исходя из условия, что электромагнитная волна, отраженная от рефлектора (зеркала), должна иметь плоский фазовый фронт. Это означает, как следует из рисунка 7.7, что оптическая длина пути между источником и плоским фронтом волны в раскрыве отражателя для любого луча должна быть одинакова.
Профиль отражающего зеркала можно определить, исходя из условия, что электромагнитная волна, отраженная от рефлектора (зеркала), должна иметь плоский фазовый фронт. Это означает, как следует из рисунка 7.7, что оптическая длина пути между источником и плоским фронтом волны в раскрыве отражателя для любого луча должна быть одинакова.
Из анализа данного рисунка следует, что уравнение профиля зеркала будет определяться соотношением
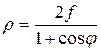 . (7.24)
. (7.24)
Выражение (7.24) является уравнением параболы в полярных координатах. Ось 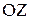 – ось параболы ‑ называется оптической осью зеркала.
– ось параболы ‑ называется оптической осью зеркала.
В том, что парабола трансформирует сферический фронт волны в плоский, нетрудно убедиться, имея в виду, что параболой называется геометрическое место точек, равноудаленных от точки (фокуса) и прямой (директрисы).
Параболические антенны разделяются на длиннофокусные и короткофокусные. В длиннофокусной антенне фокус находится вне антенны, при этом 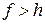 (т.е.
(т.е. 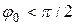 ). В короткофокусной антенне фокус находится внутри антенны, глубина зеркала
). В короткофокусной антенне фокус находится внутри антенны, глубина зеркала 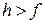 (т.е.
(т.е. 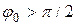 ).
).
Геометрия параболического зеркала, помимо глубины 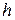 и фокусного расстояния
и фокусного расстояния 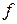 , характеризуется также размером раскрыва
, характеризуется также размером раскрыва 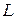 и углом полураскрыва зеркала
и углом полураскрыва зеркала 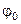 (см. рисунок 7.4). Найдем связь между
(см. рисунок 7.4). Найдем связь между 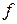 ,
, 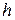 ,
, 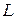 и
и 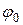 . С этой целью воспользуемся уравнением параболы в декартовой системе координат
. С этой целью воспользуемся уравнением параболы в декартовой системе координат
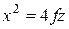 . (7.25)
. (7.25)
Подставив координаты крайней точки 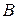 раскрыва
раскрыва 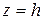 и
и  в (7.25), получим
в (7.25), получим
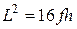 . (7.26)
. (7.26)
Из 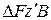 находим
находим
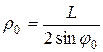 . (7.27)
. (7.27)
Подставляя (7.27) в (7.24) при 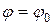 , получим
, получим
 . (7.28а)
. (7.28а)
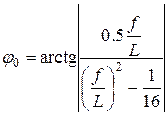 . (7.28б)
. (7.28б)
Формулы (7.11) и (7.13) позволяют по двум любым заданным геометрическим параметрам профиля зеркала найти два остальных.
Линзовые антенны
Линзовой антенной называется совокупность электромагнитной линзы и облучателя.
Линзой называют прозрачное для ЭМ волн тело, коэффициент преломления которого отличается от коэффициента преломления окружающей среды.
Линзы, используемые для преобразования сферического или цилиндрического фронта волны в плоский, называются фокусирующими.
 Принцип работы диэлектрической фокусирующей линзы ясен из рисунка 7.7,а. От источника F на линзу падает сферическая волна. Освещенная поверхность линзы выпуклая, следовательно, волна, падающая в центре, пройдет путь больший, чем волны по краям. Так как фазовая скорость волны в теле линзы в
Принцип работы диэлектрической фокусирующей линзы ясен из рисунка 7.7,а. От источника F на линзу падает сферическая волна. Освещенная поверхность линзы выпуклая, следовательно, волна, падающая в центре, пройдет путь больший, чем волны по краям. Так как фазовая скорость волны в теле линзы в 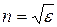 раз меньше, чем в свободном пространстве, (причем
раз меньше, чем в свободном пространстве, (причем  ), то фронт сферической волны превращается на теневой стороне линзы в плоский. Такая линза называется замедляющей.
), то фронт сферической волны превращается на теневой стороне линзы в плоский. Такая линза называется замедляющей.
Профиль замедляющей линзы определяется соотношением
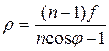 . (7.29)
. (7.29)
Здесь 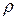 ‑ текущее расстояние от фокуса линзы до произвольной точки на освещенной поверхности линзы.
‑ текущее расстояние от фокуса линзы до произвольной точки на освещенной поверхности линзы.
Толщина линзы  определяется соотношением
определяется соотношением
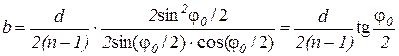 . (7.30)
. (7.30)
Данное выражение связывает между собой конструктивные параметры линзы: диаметр d, толщину b , коэффициент преломления n и угол раскрыва 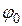 .
.
Диэлектрические (замедляющие) линзы широкополосны, однако имеют большой вес. Существенными могут быть и потери в диэлектрике. В связи с этим на практике чаще используются металлопластинчатые линзы, в которых фазовая скорость волн выше, чем в свободном пространстве (такие линзы получили название ускоряющих). Данные линзы состоят из параллельных металлических пластин, отстоящих друг от друга на расстоянии a и образующих вогнутую поверхность, как показано на рисунке 7.7,б.
Для ускоряющей линзы уравнение профиля определяется выражением:
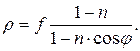 (7.31)
(7.31)
Профиль ускоряющей линзы является эллипсом.
Толщина линзы определяется по формуле
 . (7.32)
. (7.32)
Рассмотренная линза фокусирует излучение только в плоскости вектора Е. Для фокусировки в двух плоскостях одновременно необходимо от середины линзы к краям увеличивать размер t пластин (см. рисунок 7.7,б).
Недостаток ускоряющих линз ‑ их сравнительная узкополосность, т.к. коэффициент преломления зависит от 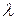
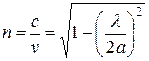 . (7.33)
. (7.33)
Для уменьшения толщины b как ускоряющих, так и замедляющих линз их зонируют, уменьшая толщину линзы ступеньками. Глубина ступеней выбирается такой, чтобы скачок фазы за счет сокращения пути луча в линзе от каждой ступеньки равнялся 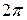 , что эквивалентно разнице в длине оптического пути соседних лучей в одну длину волны.
, что эквивалентно разнице в длине оптического пути соседних лучей в одну длину волны.
Облучатель является важным элементом зеркальной и линзовой антенн, во многом определяющим общие характеристики всей антенной системы в целом.
Требования, предъявляемые в связи с этим к облучателю, заключаются в следующем:
1.Амплитудная характеристика облучателя должна иметь минимальное излучение вне угла раскрыва зеркала антенны или линзы и должна обеспечивать требуемое амплитудное распределение в раскрыве.
2.Фазовая характеристика должна иметь четко выраженный фазовый центр, совмещенный с фокусом зеркала.
3.Желательно, чтобы облучатель имел по возможности минимальные геометрические размеры, чтобы меньше затенять раскрыв антенны.
4. Электрическая прочность облучателя должна быть достаточной для пропускания полной рабочей мощности радиосистемы без пробоя.
5. Полоса рабочих частот должна соответствовать требуемой полосе частот радиосистемы.
6. Облучатель должен иметь конструкцию, обеспечивающую его нормальную работу в любых метеоусловиях, допускать возможность герметизации фидерного тракта. Как правило, облучатель закрывают диэлектрическим кожухом.
Наиболее распространенными конструкциями облучателей параболических и линзовых антенн являются: вибраторные, щелевые и волноводно-рупорные. Иногда применяют стержневые, спиральные и другие типы антенн. В частности, облучатель зеркальной антенны одной из РЛС выполнен в виде спиральной антенны обратного излучения.
Дата добавления: 2015-11-06; просмотров: 4924;
