Гармонический осциллятор.
Систему, описываемую уравнением 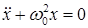 , где
, где 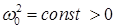 , будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:
, будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:
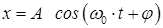 .
.
Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия.
Для гармонического осциллятора справедливы все результаты, полученные ранее для гармонического колебания.
Рассмотрим и обсудим ещё дополнительно к ним два вопроса.
Найдем импульс гармонического осциллятора. Продифференцируем выражение 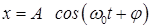 по t и, умножив полученный результат на массу осциллятора, получим:
по t и, умножив полученный результат на массу осциллятора, получим:
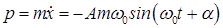 . (8.8)
. (8.8)
В каждом положении, характеризуемом отклонением “x”, осциллятор имеет некоторое значение ”p”. Чтобы найти ”p” как функцию ”x”, нужно исключить ”t” из написанных для ”p” и ”x” уравнений, Представим эти уравнения в виде:
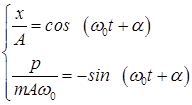 (8.9)
(8.9)
Возведя эти выражения в квадрат и складывая, получим:
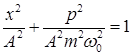 . (8.10)
. (8.10)
 Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w0”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].
Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w0”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].
Найдем теперь площадь эллипса 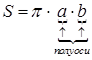 . Или
. Или
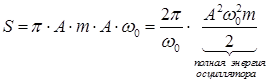 .
.
Здесь 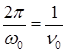 , где n0 – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.
, где n0 – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.
Следовательно, 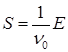 . Откуда
. Откуда
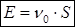 . (8.11)
. (8.11)
Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора.
8.6. Малые колебания системы вблизи положения равновесия.
Рассмотрим произвольную механическую систему, положение которой может быть задано с помощью одной величины “x”. Величиной ”x”, определяющей положение системы может быть угол, отсчитываемый от некоторой плоскости или расстояние, отсчитываемое вдоль заданной кривой.
Потенциальная энергия такой системы будет функцией одной переменной ”x”: Ep=Ep(x).
Выберем начало отсчета таким образом, чтобы в положении равновесия x=0. Тогда функция Ep(x) будет иметь минимум при x=0.
Далее разложим функцию Ep(x) в ряд по степеням “x”, причем ограничимся случаем малых колебаний, поэтому высшими степенями “x” можно пренебречь. По формуле Маклорена:
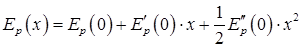 .
.
(ввиду малости “x” остальными членами пренебрегаем)
Так как Ep(x) при x=0 имеет минимум, то 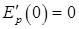 , а
, а 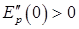 . Обозначим Ep(x) = b и
. Обозначим Ep(x) = b и 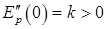 , тогда
, тогда 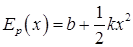 .
.
Это выражение идентично с выражением для потенциальной энергии системы, в которой действует квазиупругая сила (константу “b” можно положить равной 0).
Сила, действующая на систему, может быть определена по формуле: 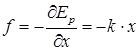 . Получено с учетом, что работа совершается за счет убыли потенциальной энергии
. Получено с учетом, что работа совершается за счет убыли потенциальной энергии 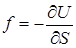 .
.
Итак, потенциальная энергия системы при малых отклонениях от положения равновесия оказывается квадратичной функцией смещения, а сила, действующая на систему, имеет вид квазиупругой силы. Следовательно, при малых отклонениях от положения равновесия любая механическая система будет совершать колебания, близкие к гармоническим.
8.7. Математический маятник.
ОПРЕДЕЛЕНИЕ: математическим маятником будем называть идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Отклонение маятника от положения равновесия будет характеризоваться углом j (рис. 8.7). При отклонении маятника от положения равновесия возникает вращательный момент 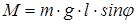 , он имеет такое направление, что стремится вернуть маятник в положение равновесия, поэтому моменту M и угловому смещению j нужно приписать разные знаки.
, он имеет такое направление, что стремится вернуть маятник в положение равновесия, поэтому моменту M и угловому смещению j нужно приписать разные знаки.
Следовательно,
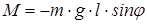 . (8.12)
. (8.12)
 Напишем теперь для маятника уравнение динамики вращательного движения (учитывая, что b – угловое ускорение равно
Напишем теперь для маятника уравнение динамики вращательного движения (учитывая, что b – угловое ускорение равно 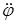 , а
, а 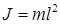 ).
).
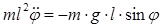
Рассмотрим малые колебания ( 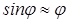 ) и введем величину
) и введем величину 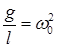 , тогда получим
, тогда получим
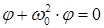
Решением этого уравнения будет функция 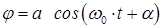
 Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.
Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.
Как следует из формулы 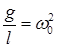 , частота колебаний математического маятника зависит только от его длины и величины “g” и не зависит от массы маятника. Учитывая, что
, частота колебаний математического маятника зависит только от его длины и величины “g” и не зависит от массы маятника. Учитывая, что 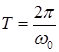 получим
получим
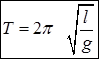 . (8.13)
. (8.13)
Дата добавления: 2015-11-04; просмотров: 1516;
