Сводка основных типов отношений
Таблица 1.
 Св-ва отноТип шения
отношения Св-ва отноТип шения
отношения
| Рефлексивность | Симметричность | Транзитивность | Антирефлексивность | Антисимметричность | Связность |
| Эквивалентность | + | + | + | |||
| Строгий Порядок | + | + | (+) | |||
| Нестрогий порядок | + | + | + | |||
| Строгий линейный порядок | + | + | (+) | + | ||
| Нестрогий линейный порядок | + | + | + | + | ||
| Строгий частичный порядок | + | + | (+) | – | ||
| Нестрогий частичный порядок | + | + | + | – |
Скобки означают, что это свойство вытекает из остальных.
Замечание. Условимся под анкетой отношения понимать указание всех основных свойств, которыми оно обладает и которыми не обладает, и соотнесение отношения к соответствующему типу, если это возможно.
Пример. Составить анкету отношений, заданных на множестве 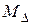 треугольником условиями:
треугольником условиями:
а) 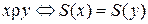 ;
;
б) 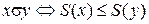 ;
;
в) 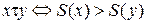 ,
,
где через 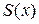 обозначается площадь треугольника
обозначается площадь треугольника 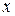 из
из 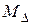 .
.
□ а) Пусть 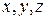 – произвольные треугольники. Имеем
– произвольные треугольники. Имеем
1) 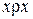 , так как
, так как 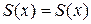 , и поэтому
, и поэтому 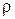 – рефлексивное отношение (словами, площади равных треугольников равны);
– рефлексивное отношение (словами, площади равных треугольников равны);
2) 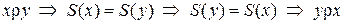
 и поэтому
и поэтому 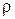 – симметричное отношение (словами, если площадь треугольника
– симметричное отношение (словами, если площадь треугольника 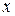 равна площади треугольника
равна площади треугольника 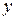 , то и площадь треугольника
, то и площадь треугольника 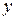 равна площади треугольника
равна площади треугольника 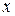 );
);
3) 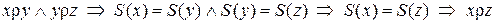 и поэтому
и поэтому 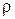 – транзитивное отношение (словами, если площадь треугольника
– транзитивное отношение (словами, если площадь треугольника 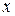 равна площади треугольника
равна площади треугольника 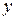 и площадь треугольника
и площадь треугольника 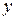 равна площади треугольника
равна площади треугольника 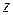 , то площадь треугольника
, то площадь треугольника 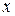 равна площади треугольника
равна площади треугольника 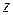 );
);
4) отношение 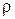 не является антирефлексивным, так оно рефлексивно и не включается в диагональ;
не является антирефлексивным, так оно рефлексивно и не включается в диагональ;
5) отношение 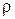 не является антисимметричным отношением, так как неравные треугольники могут иметь равные площади, т.е. истинно высказывание, отрицающее свойство антисимметричности:
не является антисимметричным отношением, так как неравные треугольники могут иметь равные площади, т.е. истинно высказывание, отрицающее свойство антисимметричности:
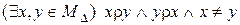 ;
;
6) отношение 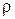 не является связным, так как существуют неравные треугольники, имеющие различные площади, т.е. истинно высказывание, отрицающее свойство связности:
не является связным, так как существуют неравные треугольники, имеющие различные площади, т.е. истинно высказывание, отрицающее свойство связности:
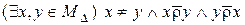 .
.
Заполнив табл. 2
Таблица 2.
 Св-ва отно-
Обозн. шения
отношения Св-ва отно-
Обозн. шения
отношения
| Рефлексивность | Симметричность | Транзитивность | Антирефлексивность | Антисимметричность | Связность |
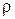
| + | + | + | – | – | – |
и сравнив ее с табл. 1, делаем вывод, что отношение 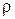 есть отношение эквивалентности на множестве
есть отношение эквивалентности на множестве 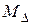 треугольников. В один класс этой эквивалентности попадают треугольники, которые имеют равные площади.
треугольников. В один класс этой эквивалентности попадают треугольники, которые имеют равные площади.
Таким образом, анкета для отношения 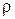 составлена.
составлена.
Ниже мы приведем анкеты для отношений 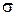 и
и 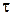 в виде уже заполненной таблицы (обоснование ее предоставляется читателю).
в виде уже заполненной таблицы (обоснование ее предоставляется читателю).
Таблица 3.
 Св-ва отно-
Обозн. шения
отношения Св-ва отно-
Обозн. шения
отношения
| Рефлексивность | Симметричность | Транзитивность | Антирефлексивность | Антисимметричность | Связность |
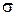
| + | – | + | – | – | – |
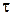
| – | – | + | + | – | – |
Сравнивая табл. 3 с табл. 1, делаем вывод, что отношения 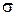 и
и 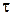 нельзя отнести ни какому указанному там типу отношений.
нельзя отнести ни какому указанному там типу отношений.
Вопросы для самоконтроля
1. Дать понятие упорядоченной пары. Определить декартово произведение двух множеств. На координатной плоскости указать множество точек, соответствующих декартову произведению 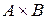 , если:
, если:
а) 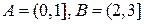 ;
;
б) 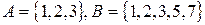 .
.
2. Дать определение бинарного отношения. На множестве 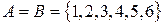 задать отношение делимости предикатом, парами, графом.
задать отношение делимости предикатом, парами, графом.
3. Сформулировать и записать на языке предикатов свойства бинарных отношений.
4. Составить анкету следующих бинарных отношений:
а) 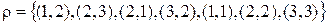 , где
, где 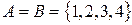 .
.
б) 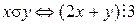 , где
, где 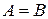 = Z.
= Z.
5. Дать определение обратного отношения. Как связаны графики 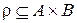 и
и 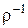 , если
, если 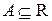 и
и 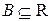 ? Привести примеры.
? Привести примеры.
6. Дать определение отношения эквивалентности. Является ли 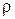 отношением эквивалентности на множестве
отношением эквивалентности на множестве 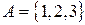 , если:
, если:
а) 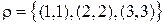 ;
;
б) 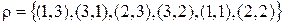 .
.
7. Выяснить, является ли эквивалентностью отношение 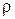 на множестве целых чисел, если
на множестве целых чисел, если 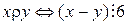 ? Если да, то указать все классы эквивалентности.
? Если да, то указать все классы эквивалентности.
8. Дать определение отношения порядка, строгого, линейного, частичного порядков.
9. Выяснить, является ли отношение делимости на множестве натуральных чисел порядком? Если да, установить его тип.
10. Что называется областью определения и множеством значений отношения 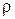 . Найти область определения и множество значений для отношения:
. Найти область определения и множество значений для отношения: 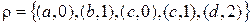 .
.
11. Какое отношение называется функцией, отображением? Что характерно для графа функции? отображения?
12. Какое отображение называется инъективным, сюръективным, биективным?
13. Выяснить является ли следующее отношение отображением:
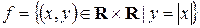 ?
?
Если да, проверить его свойства.
14. Какое отображение называется обратимым? Сформулировать условия обратимости. Привести пример.
15. Что понимается под произведением отображений? Найти произведение отображений
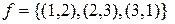 и
и 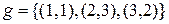 .
.
16. Дать определение бинарной алгебраической операции на множестве. Как обозначается результат действия операции? Являются ли алгебраическими на множестве Z следующие операции:
а) 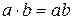 ;
;
б) 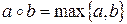 ;
;
в) 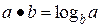 .
.
17. Сформулировать и записать свойства бинарных алгебраических операций. Выяснить, какими свойствами во множестве 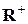 всех положительных действительных чисел обладает следующая операция:
всех положительных действительных чисел обладает следующая операция:
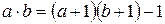 .
.
Дата добавления: 2015-11-04; просмотров: 918;
