Статические и динамические характеристики измерительных преобразователей
Статическая характеристика измерительного преобразователя — это функциональная зависимость между входной xи выходной yвеличинами в установившемся режиме. Как и любую функцию, статическую характеристику можно представить аналитически (уравнением), в виде графика или таблично. Обычно в уравнение преобразования входят конструктивные параметры. Для реального преобразователя статическую характеристику можно получить экспериментально. Для более наглядного восприятия очень широко используют графическую форму представления статической характеристики. Наиболее часто используемые статические характеристики датчиков представлены на рис. 3.1.
В общем случае статические характеристики ИП не отличаются от аналогичных характеристик обобщенных звеньев систем управления, так как сами входят в их число.
Статическая характеристика может быть линейной и нелинейной (см. рис. 2.1, а, б). При этом необходимо отличать нелинейность как требуемую функциональную зависимость (например, экспоненциальную, логарифмическую) от собственно нелинейности как погрешности линейности.
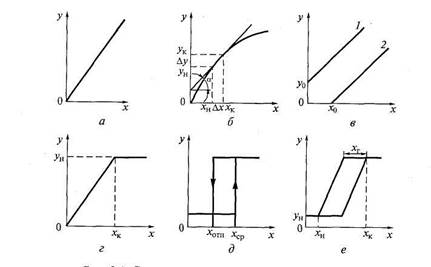
Рисунок 2.1 Статические характеристики датчиков:
а- линейная; б- не линейная; в- с сигналом холостого хода и зоной нечувствительности; г- с участком насыщения; д- релейного характера; е- с петлёй гистерезиса.
В общем случае уравнение преобразования для линейной статической характеристики имеет вид
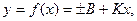
где B — постоянная; K— коэффициент преобразования.
Если B = 0, то график уравнения проходит через начало координат и ИП не имеет ни выходного сигнала холостого хода у0, ни зоны нечувствительности 0...x0 (см. рис. 2.1, а).
При B > 0 характеристика смещена относительно начала координат по оси ординат на величину выходного сигнала холостого хода y0 = В(см. рис. 2.1, в, прямая 1).
При B < 0 характеристика имеет зону нечувствительности 0...x0, в пределах которой при изменении x y= 0 (см. рис. 2.1, в, прямая 2).
Статическая характеристика может иметь участок насыщения (см. рис. 2.1, г), тогда она описывается двумя уравнениями: на участке 0...xкуравнением у = Kx; на участке x > xкуравнением y = yH.
При K = ∞ характеристика принимает релейный характер (см. рис. 2.1, д). Такая характеристика, присущая датчикам позиционного регулирования, характеризуется коэффициентом возврата:
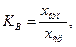
где xотп, xср - значение входного сигнала, обеспечивающие соответственно отпускание и срабатывание датчика (реле).
Ряд датчиков имеет неоднозначность хода статической характеристики при увеличении и уменьшении входной величины x (см. рис. 2.1, е). Это явление носит название гистерезиса и характеризуется соответствующим коэффициентом:
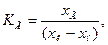
где xГ — ширина зоны неоднозначности; xк,xн— значения соответственно конца и начала рабочего диапазона входной величины.
На рис. 2.1 представлены характеристики однотактных (нереверсивных) датчиков. Характеристики двухтактных датчиков имеют вторую аналогичную ветвь, расположенную в третьем квадранте симметрично началу координат.
Нелинейную характеристику можно преобразовать в линейную (линеаризовать) или функциональную с помощью аппроксимации.
Для нелинейных характеристик коэффициент преобразования не является постоянной величиной, поэтому в этом случае используют дифференциальный коэффициент преобразования KД, под которым понимают предел отношения выходной и входной величин:

Дифференциальный коэффициент преобразования в общем случае меняется от точки к точке и определяется углом α наклона касательной к характеристике в рабочей точке; KД=tgα. Коэффициент преобразования характеризует чувствительность датчика Ks и в зависимости от наименования входной и выходной величин может быть представлен в размерном или безразмерном виде.
Если на характеристике выделить линейный участок, в пределах которого работает преобразователь, то разность между верхним и нижним значениями входного (выходного) сигнала определяет рабочий диапазон Δр его изменения, а их отношение — динамический диапазон Δд (см. рис. 3.1, б):

Порог чувствительности — это минимальное значение входного сигнала х, вызывающего появление заметного выходного сигнала у.
Погрешности датчиков делятся на основные и дополнительные. Основная погрешность датчика — максимальная разность между измеренным значением выходного сигнала yр и его истинным значением ук, определяемым по идеальной статической характеристике для данной входной величины при нормальных эксплуатационных условиях. Она может выражаться как в абсолютных единицах: Δ = yр - yИ, так и в относительных. В последнем случае она равна отношению абсолютной погрешности к истинному значению выходного сигнала:
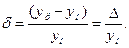
Можно использовать относительную приведенную погрешность γ, равную отношению максимальной абсолютной погрешности Δ в диапазоне измеряемой величины к верхнему значению этого диапазона yк в процентах:
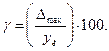
Дополнительные погрешности — это погрешности, вызываемые условиями внешней среды и внутренними процессами в деталях преобразователя. К этим процессам можно отнести: изменения температуры, влажности; колебания напряжения источника питания, механические воздействия; старение и износ материала. Дополнительная погрешность выражается обычно в процентах изменения выходной величины на определенную величину возмущающего параметра.
В зависимости от специфики применения датчиков погрешности нормируются абсолютным значением, относительным или классом точности, определяющимся обобщенной характеристикой основной приведенной и дополнительных погрешностей.
Статические характеристики позволяют оценить работу преобразователей в установившемся режиме. Однако в реальных условиях датчикам иногда приходится работать в условиях быстроменяющихся процессов, т. е. в динамическом режиме, когда на вход поступают сигналы, изменяющиеся во времени. В этих случаях начинают проявляться явления отставания выходного сигнала от входного изменения его частоты, фазы, амплитуды.
По динамическим характеристикам большинство датчиков относится к усилительным, апериодическим и колебательным звеньям первого и более высоких порядков. Наиболее используемые характеристики датчиков: частотная характеристика и передаточная функция, а параметры — постоянная времени, время запаздывания и коэффициент усиления.
Дата добавления: 2015-10-26; просмотров: 3121;
