МЕТОДЫ ОПИСАНИЯ ПРОЦЕССОВ И СРЕДСТВ ИЗМЕРЕНИЙ

Получить определенные значения величин, характеризующих исследуемый объект, и оценить их качество можно не только в ре­зультате измерения (эксперимента) с использованием технических средств, но и теоретическим путем. Например, составив математиче­ские модели объекта и средства измерений и решив задачу «взаимо­действия», можно получить некоторый результат (в виде чисел, таб­лиц, диаграмм и т. д.), характеризующий исследуемый объект. Сле­довательно, необходимость использования СИ в данном случае отпадает.

Оба эти метода — экспериментальный и теоретический — в насто­ящее время используются довольно широко. Экспериментальный — является неотъемлемой частью контроля параметров автоматизи­рованных процессов, измерений в научных исследованиях, окружаю­щей среде и т. д., а также управления ими. Теоретический — исполь­зуется в основном при разработке средств измерений, оценке их ка­чества и оптимизации параметров.

Для оценки качества измерения и определения требований к СИ неизбежно приходится использовать модели процесса из­мерения, выделяя главные явления и факторы. Рассмотрим две из них: детерминистскую и информационную.

Детерминистская модель строится при следующих ограниче­ниях [5]: 1) измеряемая физическая величина сохраняет неизмен­ное значение на протяжении всего цикла измерения; 2) время изме­рения не ограничено, и сравнение с мерой может выполняться как угодно долго и тщательно; 3) внешние условия и влияющие на ре­зультат измерения факторы точно определены.

Однако в связи с бурным развитием техники практически все измерения, связанные с задачами контроля параметров технологи­ческих процессов при автоматизированном управлении производ­ством, многие виды измерений при исследованиях в различных об­ластях физики, химии, биологиии т. д. представляют собой измерения изменяющихся во времени физических величин. Следовательно, реальные процессы отличаются от модели.

Поэтому в настоящее время все в большей мере используется другая — вероятностная (информационная) модель [5] процесса измерения, в которой: 1) измеряемая физическая величина рассмат­ривается как случайный процесс, содержащий интересующую нас информацию об объекте, и описывается случайной последователь­ностью действительных значений или же обобщенными характерис­тиками (математическое ожидание, дисперсия); 2) истинное значение величины может оставаться неопределенным на данном этапе изме­рения; 3) измерение рассматривается как последовательность опе­раций, время выполнения которых ограничено и конечно; 4) непо­средственное сравнение с мерой в общем случае неосуществимо; 5) характеристики измерительного устройства могут изменяться во времени и под влиянием переменных внешних факторов.

Из сравнения двух моделей процесса измерения следует, что информационная модель является наиболее общей, а классическая детерминистская — ее частным случаем.

Хотя при информационном подходе возникает необходимость описания сложных вероятностных связей, однако, во-первых, по­является возможность оценки качества измерения непрерывных меняющихся во времени величин; во-вторых, информационное опи­сание с учетом измерительного преобразования, при котором рас­сматриваются потери информации в каждом звене, дает однозначную характеристику качества преобразования при любом виде сигнала. Большие преимущества информационный подход дает при анализе, дискретизации, квантовании и восстановлении измеряемых сигналов.

При теоретическом исследовании процесса измерения в общем случае должны быть описаны объект измерения и СИ, а также оп­ределены методы анализа, оценки качества, оптимизации и т. д. как самих результатов, так и параметров СИ.

Объект измерения — это сложное многогранное явление или про­цесс, характеризующийся множеством отдельных параметров, каж­дый из которых может быть измерен в отдельности, но в реальных условиях действует на измерительный прибор совместно с осталь­ными параметрами. Измеряемая величина — это один из парамет­ров объекта, который выбран для измерения. Измеряемая величина при информационном подходе в общем случае описывается как слу­чайная функция времени, то есть случайный процесс. Следователь­но, для описания объекта измерения необходимо использовать из­вестные методы теории случайных процессов. Вместе с тем, для оцен­ки качества, например [8], СИ и в некоторых практических случа­ях возможно описание входной величины как детерминированной (единичное ступенчатое воздействие, единичный импульс, синусои­дальный сигнал и др.). Такое описание можно рассматривать как частный случай общего описания - случайного процесса.

Одной из основных характеристик СИ является дифференциаль­ное уравнение [8], на основании или с использованием которого мо­гут быть получены или описаны практически все другие характеристики и (статические, частотные, переходная |характеристика и т. д.). Если рассматривать СИ как последовательную цепь преобразователей, то оно может быть описано совокупностью (системой) дифференциальных и алгебраических уравнений и других соотношений. Следовательно, в общем слу­чае описание СИ — это процесс получения математической модели, представляющей собой одно или систему дифференциаль­ных уравнений и других соотношений и являющейся основой для исследования процесса преобразования (передачи) информации и оценки качества.

Оставляя в стороне основы теории сложных информационно- измерительных систем, составной частью которых можно рассматривать измерительные приборы (как приборы первичной информа­ции), остановимся на некоторых общих методах их описания и исследования.

В настоящее время для составления математической модели, рас­чета и проектирования средств измерений широко используется структурный метод [9, 10, 11, 22, 23, 53]. В основу метода положен принцип измерительных преобразований и представления средства и измерений или устройства в виде взаимосвязанной цепи преобразователей.

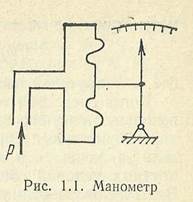
Например, простейший механический манометр (рис. 1.1), в котором давление р преобразовывается в силу F, затем — в де­формацию мембранной коробки є, а перемещение жесткого центра Мембраны через передаточный механизм — в перемещение х; и про­порциональный ему угол поворота стрелки указателя 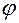, можно представить в виде цепочки преобразований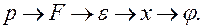

Затем, определив функциональные зависимости

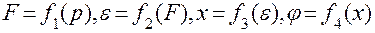(1.1)

поручить систему или одно уравнение (в общем случае — математическую модель), описывающие зависимость выходной величины от входной: .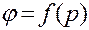

С учетом изменения переменных во времени эта зависимость примет вид

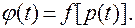
Приняв для общности за входную и выходную величины некоторые обобщенные переменные X (t) и у (t), получим

(1.2)

Математическая модель типа (1.2) описывает зависимость между выходной и входной величинами во временной области. Используя, например, преобразования –Фурье и Лапласа, можно получить математические модели в частотной и комплексной областях:

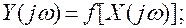
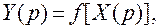
где 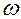— круговая частота 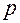— комплексная переменная.

Когда средство измерений имеет более сложную структуру или используются унифицированные преобразователи ГСП с известными характеристиками типа (1.1), составление его математической мо­дели заключается в объединении этих зависимостей с учетом кон­кретных условий сопряжения и совместимости преобразователей. В случае разработки новых ИП или приборов зависимости типа (1.1) должны быть определены, например, на основании законов физики, соотношений между энергиями, силами, скоростями и т. д.

Структурный метод является примером системного подхода или деления СИ на уровни и элементы (преобразователи). Для информа­ционно-измерительных систем (комплексных средств измерений) возможно появление следующего уровня, состоящего из устройств типа, приведенного на рис. 1.1. В этом случае для более сокращен­ной записи, естественно, с меньшей детализацией, возможно ис­пользование содержательных логических схем алгоритмов, матрич­ной записи и др.

С учетом многообразия параметров, которые необходимо учесть при описании средства измерений, математическая модель типа (1.2) в общем случае имеет вид

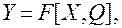
где У = (у₁ у₂, ..., у_т), X = (х₁, х₂, ..., х_п), Q = (q₁, q₂, ..., q_l) — векторы выходных, внешних и внутренних параметров; m, n, l — количество выходных, внешних и внутренних параметров соответ­ственно.

Одной из наиболее общих и важных характеристик процесса и средства измерений являются информационные характеристики, так как во многих случаях они позволяют оценить предельные воз­можности исследуемого метода измерения.

В качестве количественной меры информации может рассматри­ваться разность неопределенностей до и после эксперимента. Сле­дуя классической методике, принятой в теории информации, оха­рактеризуем распределение вероятностей до эксперимента безу­словной, или априорной, энтропией (неопределенностью) входной H (X) и выходной Н (Y) величин прибора, а после эксперимента — условной, или апостериорной, энтропией входной Н (Х/У) величи­ны при задании выходной и выходной Н (У/Х) величины при зада­нии входной. Тогда количество информации может быть определе­но [13] как

I=Н(Х) — Н (Х/У) =Н(У) — Н (У/X).(1.3)

Для информационной оценки аналогового i-го преобразовате­ля (1.3) имеет вид

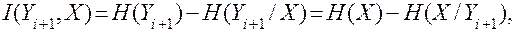(1.4)

где 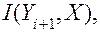— количество информации в процессе на выходе преобразователя относительно истинного значения; 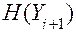— безусловная энтропия на выходе (i + 1)-го преобразователя; 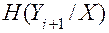- среднее значение условной энтропии процесса на выходе (i + 1)-го преобразователя при задании истинного значения; 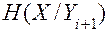— среднее значение условной энтропии истинного значения измеряе­мой величины при задании величины на выходе (i + 1)-го преобразователя.

Приведенные зависимости позволяют выполнять оценку двух видов информации: 1) количества информации относительно X в процессе, состоящем из суммы истинного значения X и погрешности Y; 2) количества информации в процессе на выходе преобразователя (прибора) относительно выходного сигнала.

К основным нормируемым метрологическим характеристикам СИ (наряду с другими) относятся погрешности. Энтропийное зна­чение погрешности может быть получено на основании соотноше­ний (1.3), (1.4). Математические модели погрешностей в статическом и динамическом режимах могут быть получены на основании математических моделей средств измерений типа (1.2). Погрешность средств измерений при этом следует рассматривать как разность между истинным (идеальным) и реальным (действительным) значе­ниями выходной или входной величины.

В общем случае выходная величина прибора или преобразовате­ли у (t) является некоторой функцией входной величины x(t) и может быть записана как

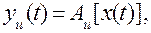(1.5)

где — идеальный оператор преобразования.

Аналогично реальная зависимость

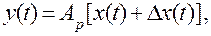(1.6)

где 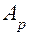— реальный оператор преобразования; 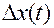— погрешность на входе.

Тогда погрешность на выходе

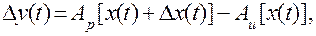(1.7)

Следовательно, погрешность на выходе зависит от разности опе­раторов А_р и А_И и погрешности на входе 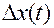. Такая модель может быть положена в основу как оценки качества результатов, так и нахождения оптимальных значений А_р, зависящих от конструк­тивных параметров технических средств.

Погрешность в общем случае является случайной величи­ной, что обусловлено случайным характером 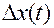и возможностью Изменения 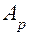под воздействием внешних и внутренних факторов.

И основу дальнейшего рассмотрения положим три вида методов и моделей математического описания и исследования СИ: 1) модель для определения зависимости между выходом и входом; 2) модель определения информационных характеристик; 3) модель для определения погрешностей процесса и средств измерений, вкоторой используется аппарат теории вероятностей и теории информации.

При этом вопросы составления и анализа математических моде­лей объекта и СИ будем рассматривать во временной, частотной и комплексной областях.