МІКРООПЕРАЦІЇ В РЕГІСТРАХ

Мікрооперація – елементарна дія, яка виконується в комп’ютерах в одному машинному такті.

Для запису інформації від декількох джерел на вході кожного тригера ставлять додаткові комбінаційні схеми, які створюють вхідну логіку регістра. Запис кожного слова ініціюється відповідним керуючим сигналом 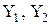та ін.

Для запису в регістр кодів А, В потрібно реалізувати таку функцію:

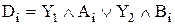, (1)

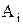де і 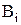– двійкові розряди слів А і В;

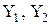– сигнали керування приймання слів А і В відповідно.

Схема вхідної логіки і-го розряду регістра на основі рівняння (1) приведена на рисунку 12.1.

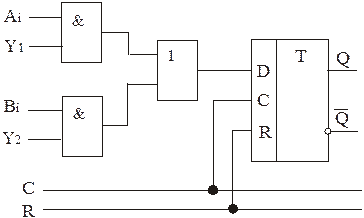
Рис. 12.1 – Схема вхідної логіки і-го розряду регістра

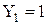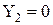, запис коду ;

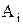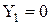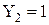, запис коду .

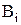Зчитування інформації

Для реалізації мікрооперації зчитування до виходів кожного тригера підключаються комбінаційні схеми, які створюють вихідну логіку регістра.

Схеми вихідної логіки будуються на основі таких порозрядних логічних рівнянь:

– для зчитування однофазним прямим або оберненим кодом

;

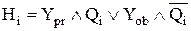– для зчитування парафазним прямим або оберненим кодом

;

;

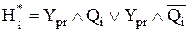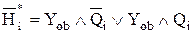де 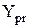і 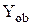– керуючі сигнали відповідно прямого або оберненого коду;

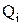, – пряме та інверсне значення виходу і-го розряду регістра;

– розряд однофазної шини даних;

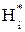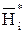, – розряди парафазної шини даних.

Керуючі сигнали 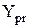і 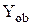не повинні збігатися в часі.

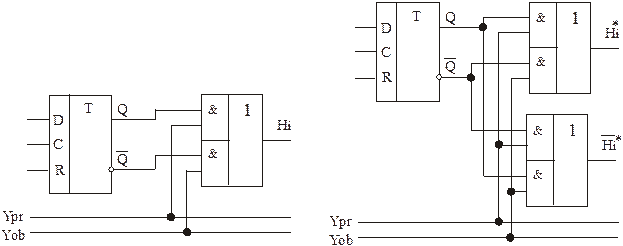
а) б)

Рис. 12. 2 – Схеми вихідної логіки і – го розряду регістра для зчитування інформації: а) однофазним кодом; б) парафазним кодом.

Логічні операції в регістрах

В регістрах можуть виконуватись такі порозрядні (без перенесень) логічні мікрооперації над словами 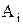і 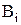: логічного додавання і множення:

, ;

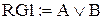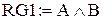– додавання за модулем два і його заперечення:

, ;

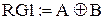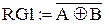– інверсія слова .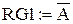

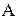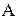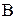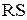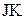Логічні мікрооперації передбачають наявність першого слова в регістрі. З врахуванням цього логічне додавання слів і в регістрі на - або - тригерах з однофазним записом виконується введенням слів 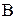без попереднього скидання.

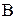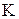Логічне множення реалізується падаванням інверсних значень розрядів слова на входи (або ) тригерів регістра. Якщо значення 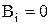то 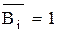і відповідно тригери обнуляються, що і потрібно для порозрядного логічного множення.

Мікрооперації за модулем два і його заперечення реалізуються в регістрах на 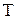- тригерах. Спочатку записується слово 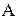, а потім без попереднього скидання по логічному входу вводиться слово 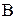. Після цього на прямих виходах тригерів фіксується результат операції 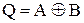а на інверсних виходах .

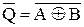Мікрооперація інвертування складається з подавання імпульсу на всі 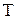- входах тригерів регістра, в яких зберігається слово А. В результаті на прямих виходах тригерів встановлюється результат згідно із співвідношення .

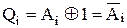Мікрооперація зсуву.

Зсув – це одночасне просторове переміщення двійкового слова в розрядній сітці із збереженням порядку слідування нулів і одиниці. Мікрооперації зсуву використовують у процесі виконання команд множення, ділення і нормалізації. Крім того з допомогою зсуву здійснюється перетворення паралельного коду в послідовний або навпаки. Зсув слова може виконуватись вправо (у бік молодших розрядів) або вліво ( у бік старших розрядів). 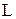Позначимо однорозрядні мікрооперації зсуву вправо і вліво символами і відповідно. Розрізняють правий і лівий арифметичний ( 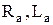), логічний ( ) і циклічний ( 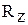, 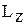) зсуви слова.

Нехай в регістрі А записано слова ,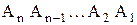

де 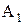– молодший розряд; 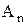– старший розряд.

Символічно мікрооперації зсуву записуються таким чином:

– арифметичні зсуви (знаковий розряд не зсувається:

;

;

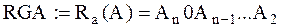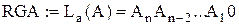– логічні зсуви (одночасно зсуваються всі розряди);

;

;

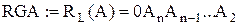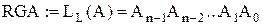– циклічні зсуви (між старшим і молодшим розрядами є кільцевий зв’язок)

;

.

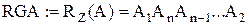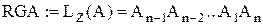Арифметичні та циклічні зсуви переважно використовуються при виконанні команд в процесорах, а логічні зсуви забезпечують перетворення послідовного коду в паралельний і навпаки.