Потери энергии на местную корону
Увеличением диаметра проводов и снижением напряженности поля на их поверхности нельзя исключить коронного разряда при неблагоприятных атмосферных условиях. Более того, даже при хорошей погоде не может быть исключена корона, например, в местах повреждения поверхности провода и арматуры гирлянд, на элементах крепления, т.е. в точках местного усиления поля. Такую корону называют местной в отличие от общей короны, существующей на всей поверхности проводов при Е > Ен.
Поскольку годовые потери энергии на корону составляют заметное значение и могут достигать 40% от потерь на нагрев проводов, они оказывают влияние на технико-экономические характеристики линии электропередачи и их необходимо учитывать.
Оценка потерь энергии на корону производится на основе экспериментально полученных данных. Существует несколько методов расчета потерь на местную корону. В одном из способов, разработанных во ВНИИЭ, используются обобщенные характеристики потерь для разных погодных условий. Выделяются четыре группы погоды: хорошая погода (без осадков); сухой снег; дождь и мокрый снег; изморозь, гололед и иней. Для трассы линии электропередачи определяются по метеорологическим данным продолжительности отдельных видов погоды в часах: хорошей погоды hhx, снега hc, дождя hд, изморози hи (табл. 1). Затем по отношению EmaxjEн из кривых (рис. 9) находят удельные потери мощности, для разных погодных условий, а затем среднегодовые потери энергии на корону.
Продолжительность усредненных характеристик погоды. Таблица 1.
| Группа | Годовая продолжительность | Годовые потери энергии при данной погоде, % общих потерь | |
| ч | % | ||
| Хорошая погода | 81,3 | ||
| Сухой снег | 9,1 | ||
| Дождь | 5,7 | ||
| Изморозь | 3,9 |
|
|
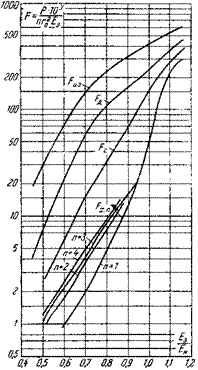
Рис. 9. Функция потерь мощности на корону для разных групп погоды:
Fх.п – хорошая погода; Fд – дождь и мокрый снег; Fс – снег;
Fиз – изморозь – независимо от числа проводов в фазе
Теоретический анализ показывает, что потери Р для одиночных проводов выражаются функциональной зависимостью:
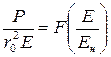 , (12)
, (12)
где r0 – радиус провода;
Е – напряженность на поверхности провода;
Ен – начальная напряженность короны.
Обработка данных, полученных на опытных пролетах на проводах различных сечений, позволила найти форму функции F:
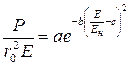 , (13)
, (13)
где a, b, c – эмпирические коэффициенты.
Для расщепленных проводов расчет усложняется вследствие несимметрии поля около проводов в пучке. Напряженность поля по периметру провода изменяется согласно формуле
Е0 = Еср(1 + Аcosq), (14)
где Еср – средняя напряженность поля на поверхности провода;
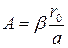 (15)
(15)
b находится по табл. 2; r0, a и q показаны на рис. 10.
Значение коэффициентов b и k и эквивалентного радиуса rэ
для расщепленной фазы. Таблица 2.
| Число проводов в фазе n | |||
| Коэффициент b | 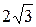
| 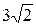
| |
| Коэффициент k | 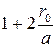
| 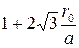
| 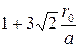
|
| Эквивалентный радиус rэ | 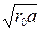
| 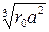
| 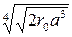
|
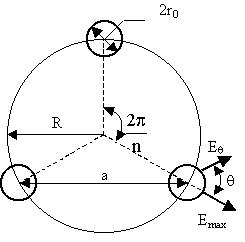
Рис. 10. Расположение расщепленных проводов в пучке
Можно, предположить, что на отрезке dl = rdq поверхности провода корона развивается так же, как на одиночном проводе с той же напряженностью поля Еq. Если принять указанное предположение, то потери dPq на участке dl, будут определяться по формуле:
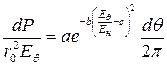 , (16)
, (16)
откуда:
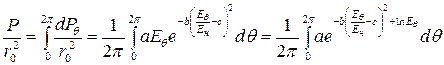 . (17)
. (17)
Для упрощения расчетов аппроксимируем функцию 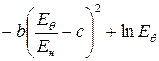 прямой
прямой 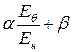 , где a и b находятся из условия наименьшего квадратичного отклонения кривых. Следовательно:
, где a и b находятся из условия наименьшего квадратичного отклонения кривых. Следовательно:
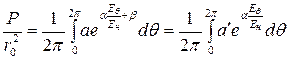 . (18)
. (18)
Если теперь подставить в (18) функцию Е0 = Еср(1 + Аcosq) и учесть первые два члена разложения в ряд подынтегрального выражения, то получим:
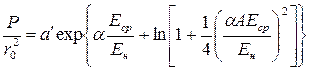 . (19)
. (19)
Для эквивалентного одиночного провода при аналогичных операциях, выраженных (18)…(19), имеем:
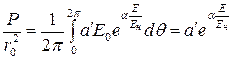 . (20)
. (20)
Приравнивая (19) и (20), получаем:
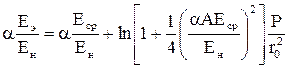 , (21)
, (21)
откуда находим значение Еэ. Так как 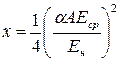 << 1, то можно положить
<< 1, то можно положить
ln(1 + x) » x и окончательно находим:
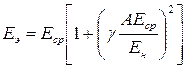 , (22)
, (22)
где 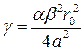 . (23)
. (23)
Значение коэффициента a по опытным данным в среднем определено равным 8,7.
Из изложенного следует, что формула потерь на корону на проводе расщепленной фазы совпадает с формулой потерь на одиночном проводе при подстановке вместо Е величины Еэ, определенной по формуле (22). Следовательно, для всех n проводов расщепленной фазы формула (13) приобретает вид:
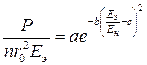 . (24)
. (24)
На практике предпочитают вести расчет не по формулам, а по опытным кривым. В данной методике эти опытные кривые выражаются функциональными зависимостями:
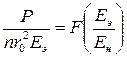 . (25)
. (25)
Потери на корону зависят от погоды. Учитываются следующие основные виды погоды: 1) хорошая погода (без осадков); дождь (включая мокрый снег); 3) снег; 4) изморозь. Функции Fх.п, Fд, Fс, Fиз для указанных видов погоды построены на рис. 9. Кривые на рис. 9 построены как средние по опытным точкам (на рисунке не показаны) для проводов различных сечений и число проводов в пучке равно 1, 2, 3, 4. Для плохой погоды (дождь, снег, изморозь) разброс опытных точек относительно кривых незначителен. Это показывает, что выбранные критериальные координаты, в частности величина Еэ, хорошо отображают физические процессы, определяющие потери на местную корону. Для хорошей погоды, при которой потери вообще малы, наблюдается существенный разброс опытных точек, в связи с чем оказалось необходимым построить кривые для n, равного 1, 2, 3, 4.
Отметим, что при определении потерь в условиях хорошей погоды начальная напряженность Ен определяется по формуле (2) для действительной плотности воздуха d в данном районе. В условиях плохой погоды Ен также вычисляется по формуле (2), но в этой формуле полагается d = 1, поскольку коронные потери при этих видах погоды мало зависят от давления и температуры воздуха.
Так как потери на корону зависят не только от вида погоды, но и от интенсивности осадков, то кривые на рис. 9 дают усредненные значения при погоде данного вида. На коронные потери, в частности при изморози, оказывает влияние также токовая нагрузка линии, подсушивающая провода, однако количественные сведения об этом влиянии недостаточны. Поэтому влияние токовой нагрузки кривые на рис. 11 не учитывают.
Дальнейший расчет основывается на продолжительности в году различных групп погоды. Обозначим эти продолжительности через Тх.п, Тд, Тс, Тиз в часах соответственно для хорошей погоды, дождя, снега, изморози. В среднем при типовом проектировании линий в районах с умеренным климатом можно принять продолжительность хорошей погоды Тх.п = 7235 ч, дождя и мокрого снега Тд = 500 ч, снега Тс = 800 ч, изморози Тиз = 225 ч.
Среднегодовые потери мощности на корону трехфазной линии определяются суммированием потерь при различных погодах по следующей формуле
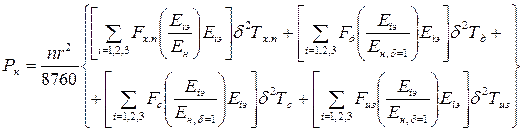 , кВт/км. (25)
, кВт/км. (25)
В этой формуле Е1э, Е2э, Е3э – эквивалентные напряженности электрического поля на поверхности проводов фаз 1, 2, 3. Функции Fх.п, Fд, Fс, Fиз находятся по кривым рис. 9 в зависимости от значений Eiэ/Ен.
Имеется упрощенная формула определения потерь на корону
Рк = n2r2(Pх.п Тх.п + РдТд + РсТc + PиТиз),
где n – общее число проводов в трех фазах линии;
r – радиус проводов;
Pх.п, Рд, Рс,Pи – удельные потери на корону при различных видах погоды.
Среднегодовая мощность потерь на корону, кВт/км, равна:
Рс.т = Рк/8760. (26)
Усредненные данные по погодным условиям для средней полосы европейской части России и Западной Сибири приведены в табл. 1. Продолжительность изморози невелика, однако потери энергии при ней составляют значительную часть среднегодовых потерь.
В оценочных расчетах потерь энергии на корону начальная напряженность для расщепленных проводов определяется по (1), а максимальная рабочая – по (10) и (11). Для одиночных проводов фаз начальная напряженность короны определяется по (1), а рабочая напряженность электрического поля – по (10) при n = 1 и rэ = 1. Напряженности рассчитываются в амплитудных значениях.
В технико-экономических расчетах рекомендуется учитывать потери на корону, если EmaxjEн £ 0,5. Экономически приемлемые потери мощности на корону имеют место при
EmaxjEн £ 0,9, (27)
и это соотношение является определяющим при выборе проводов линий электропередачи по условию ограничения потерь на корону.
Дата добавления: 2015-10-15; просмотров: 2547;
