Компандирование в ЦСП
Принципы компандирования кратко были рассмотрены в подразделе 4.1.2. Здесь этот вопрос рассмотрим более подробно. При равномерном квантовании шаг квантования D одинаков как для малых, так и для больших значений входных сигналов. Это приводит к появлению избыточности при передаче, которая проявляется следующим образом:
- число отсчетов n в заданном динамическом диапазоне равномерно распределено и при заданных критериях качества будет составлять n = 2000–4000;
- защищенность системы передачи по отношению к шумам квантования
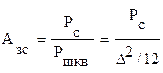 ,
,
при постоянном D будет увеличиваться с ростом амплитуды и, соответственно, мощности входного сигнала Рc, т.е. будет не постоянной. Таким образом, сильные сигналы передаются с лучшей помехоустойчивостью;
- значения входного сигнала Uc являются случайной величиной. Вероятность их появления характеризуется плотностью р(Uc) (рисунок 4.13), причем вероятность появления больших значений невысока. Это объясняется тем, что мы произносим громкие звуки гораздо реже, чем тихие. Поэтому шумы квантования для больших значений Uc не так существенны, как для малых.
Все эти факторы обосновывают применение нелинейного кодирования или неравномерного квантования.
Основные требования, предъявляемые к таким кодерам:
- восьмиразрядная кодовая комбинация;
- возможность регистрации полярности сигнала;
- минимизация шумов квантования;
- слабая зависимость защищенности от шумов квантования в заданном динамическом диапазоне;
- компрессия должна быть совмещена с кодированием.

В практике нелинейного кодирования можно использовать следующие методы:
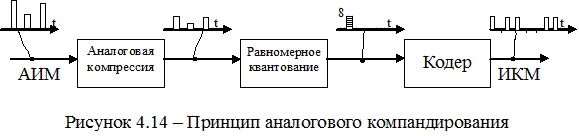
1.Аналоговое компандирование (рисунок 4.14).
Здесь вначале с помощью аналогового компрессора сжимается динамический диапазон входного сигнала, затем производится равномерное квантование с числом уровней квантования n = 28 = 256 и кодирование. Если сигнал биполярный, то применяют симметричный двоичный код, когда первый разряд используется для передач знака сигнала, а остальные семь для передачи его значения. На приемном конце используется обратная операция экспандирования. Поэтому весь процесс сжатия и расширения динамического диапазона называют компандированием.
В современных ЦСП находят применение две логарифмические характеристики (рисунок 4.15) компандирования y=f(x), где
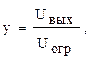 x=
x= 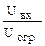 ,
,
1) А – типа
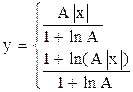
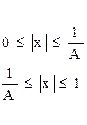 ,
,
где А = 87,6;
А и m – параметры компрессии, характеризующие степень сжатия;
Uогр – уровень ограничения входного сигнала.
2) m – типа
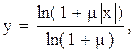
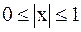 ,
,
где m=255.
Характеристика компандирования типа А используется в ЦСП европейской иерархии, а типа m – североамериканской. В связи с глобализацией телекоммуникационных систем современные ЦСП поддерживают как m, так и А кодирование.
 |
2.Нелинейное компандирование.
Этот способ сжатия заключается в том, что плавную характеристику компрессора заменяют кусочно-ломаной кривой и процесс сжатия динамического диапазона совмещают с кодированием так, что на выходе устройства появляется восьмиразрядный двоичный код. Такие компандеры наиболее широко применяются в современных цифровых системах передачи и выполняются с использованием как m, так и А-характеристик.
Характеристика А-компрессии для положительных значений входного сигнала приведена на рисунке 4.16.

Здесь ломаная кривая содержит 8 сегментов для положительных значений входного сигнала и столько же отрицательных. Нумеруются сегменты так: 0,1,2..7. Каждый сегмент с номером Nc содержит 16 позиций с одинаковым шагом квантования DN. Для удобства цифрового кодирования при переходе от сегмента к сегменту шаг квантования увеличивается в два раза. Поскольку в выходном сигнале шаг квантования одинаков во всех сегментах, угол наклона отрезков прямых в соседних сегментах должен отличаться в два раза. Для А-характеристики компрессии это условие ближе всего для значения параметра А=87,6. На практике сегменты с номерами 0 и 1 имеют одинаковый наклон и одинаковый шаг квантования D0. Поэтому реально А-характеристика имеет не 16, а 13 сегментов и часто ее обозначают А=87,6/13.
Каждый сегмент характеристики А=87,6/13 начинается со значения эталонного напряжения UэтN. Значения UэтN и другие характеристики приведены в таблице 4.2.1, где они даны относительно минимального шага квантования D0.
Таблица 4.1 Характеристики компрессии
| № сегмента | Кодовая комбинация N сегмента XYZ | 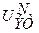
| Шаг квантования DN | Сигнал коррекции |
| 0.5 0,5 |
Максимальное значение входного сигнала 2048 D0, а выходной сигнал имеет 128 положительных и 128 отрицательных отсчетов (всего 256).
Структура кодовой комбинации А=87,6/13 имеет вид
| P | X | Y | Z | A | B | C | D |
где Р – знаковый разряд (1 – для положительных значений; 0 – для отрицательных),
XYZ – кодовая комбинация N сегмента,
АВС D – код номера позиции входного сигнала внутри сегмента.
Так, например, код 00110101 обозначает сигнал с отрицательным значением в сегменте с Nc=3 и позицией внутри сегмента N=5. Значение входного сигнала в соответствии с рисунком и таблицей будет
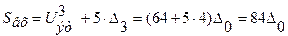 .
.
Поскольку шаг квантования D3 = 4, то код 00110101 будут давать также значения 85D0, 86D0 и 87D0. Ошибка квантования будет меняться от 0 до 3D0. Для ее компенсации при декодировании вводится сигнал коррекции, равный половине шага квантования 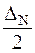 . В данном примере сигнал коррекции равен 2D0.
. В данном примере сигнал коррекции равен 2D0.
Операции нелинейного компандирования и экспандирования реализуются в нелинейных кодеках взвешивающего типа. Суть кодирования состоит в последовательном сравнении входного отсчета с набором эталонных напряжений.
Процесс кодирования включает три этапа:
1) формирование знакового символа (такт 1);
2) формирование кода номера сегмента XYZ (такты 2–4), путем сопоставления входного сигнала с эталонными напряжениями сегментов UэтN;
3) формирование кода номера позиции внутри сегмента АВСВ (такты 5–8), когда к эталонному напряжению UэтN добавляются эталонные напряжения, соответствующие позициям внутри сегмента, и происходит их сравнение с входным отсчетом.
3. Нелинейное кодирование.
Здесь входной сигнал подвергается равномерному квантованию с большим числом разрядов n=12. Кодер преобразует дискретные амплитудные отсчеты во временной 12-позиционный двоичный код. В цифровом компрессоре этот код преобразуется в 8-разрядный нелинейный код по законам А или m. Способ преобразования для закона А показан в таблице 4.2.
Таблица 4.2 - Нелинейное кодирование
| N сегмента | Код | |||
| 12-разрядный | 8-разрядный | |||
| XYZ | ||||
| Р 0 0 0 0 0 0 0 A B C D P 0 0 0 0 0 0 1 A B C D P 0 0 0 0 0 1 A B C D x P 0 0 0 0 1 A B C D x x P 0 0 0 1 A B C D x x x P 0 0 1 A B C D x x x x P 0 1 A B C D x x x x x P 1 A B C D x x x x x x | P P P P P P P P | 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 | A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D |
Основная процедура нелинейного кодирования сводится к следующему:
1) разряд «Р», определяющий знак, остается неизменным;
2) все нули после разряда «P», как незначащие, отбрасываются;
3) вместо них вставляется комбинация XYZ, определяющая номер сегмента в двоичном коде;
4) все старшие значащие разряды ABCD переписываются без изменений вслед за символами XYZ;
5) все остальные младшие разряды, помеченные знаком «х», отбрасываются вне зависимости от их значения. Таким образом, ошибка квантования возрастает с номером сегмента.
Нелинейное декодирование осуществляется так. По структуре кодовой комбинации P XYZ ABCD определяется знак отсчета и номер сегмента (по XYZ). Для известного номера сегмента задается эталонное напряжение UЭТN, соответствующее нижней границе N сегмента. После этого по известной комбинации ABCD определяется положение отсчета внутри сегмента. Наконец с целью минимизации ошибки квантования добавляется напряжение, равное половине шага квантования в данном сегменте DN. С учетом сказанного напряжение на выходе декодера можно представить в виде:
UАИМ= 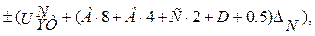
где A,B,C,D принимают значение 0 или 1, а UNЭТ и DN для А-компрессора определены ранее. В качестве примера рассмотрим кодирование и декодирование значения АИМ сигнала:
UАИМ = +934 D 0 . В двенадцати разрядном коде оно будет иметь вид:
(+1×29+1×28+1×27+1×25+1×22+1×21)
В соответствии с таблицей 4.2.2 номер сегмента N=6 и первый нуль заменяются на 110, следующие за ними четыре значения 1110 остаются, а остальные значения отбрасываются. Восьмиразрядный код принимает вид
P XYZ ABCD
1 1 1 0 1 1 01
При декодировании получим
UАИМ = +512×D 0+(1×8+1×4+0×2+1×1+0.5)×32×D 0 = (512+432)×D 0 = 944×D 0
Ошибка при восстановлении составила +10 D 0, что меньше половины шага квантования D6=32.
Дата добавления: 2015-10-13; просмотров: 1682;
