Внезапное расширение трубопровода

Частицы жидкости, пройдя сечение I, наталкиваются на более медленные частицы в широкой части трубопровода и приобретают поперечное перемещение. В начале широкого участка трубопровода в углах образуется вихреобразный поток с интенсивными потерями механической энергии на трение и, следовательно, нагрев жидкости. Определим потери напора на сопротивлении. При этом не будем учитывать трение жидкости о стенки трубопровода и примем, что поток имеет близкое к равномерному распределение скорости по сечениям I и 2.

Применим к объему жидкости, заключенному между сечениями I и 2, теорему о потере энергии при неупругом ударе: импульс сил действующих на объем в направлении оси потока, равен изменению количества движения: ,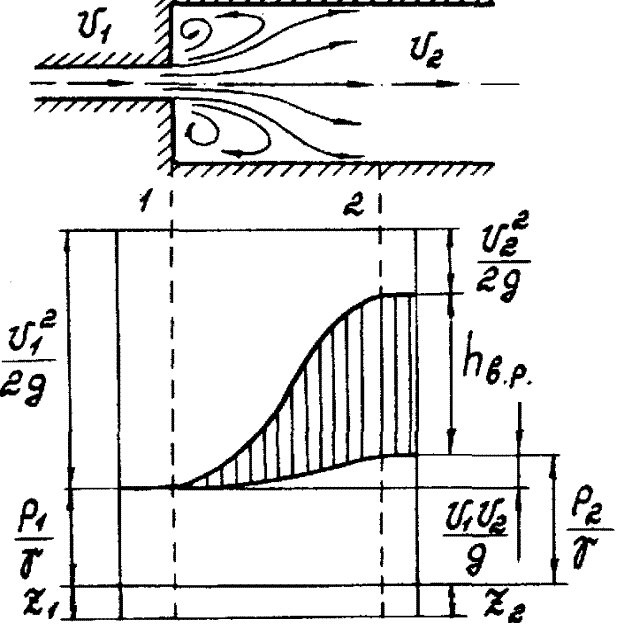

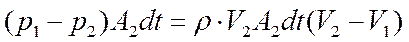где А₂ - площадь сечения2; dt - время импульса V₁ и V₂ - средние скорости до и после сопротивления.

Приводя это соотношение к структуре уравнения Бернулли для вязкой жидкости, получаем

.

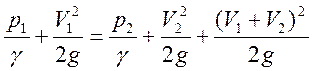Сравнивая с уравнением Бернулли, приходим к выводу о том, что местная потеря удельной энергии (напора) на внезапном расширении равна скоростному напору потерянной скорости (V₁ - V₂):

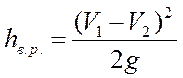
При внезапном расширении потока происходит процесс преобразования кинематической энергии в потенциальную с низким КПД, падающим при увеличении разности выходного и входного диаметров.

Перейдя к структуре формулы Вейсбаха, получим:

.

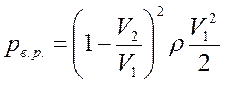Учитывая уравнение неразрывности потока, приходим к выражению для коэффициента сопротивления внезапного расширения:

,

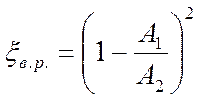где А₁, и А₂ - площади живых сечений на входе и выходе сопротивления. Если А₁>>А₂ , то 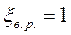, т.е. при истечении из канала в широкое затопленное пространство теряется весь скоростной напор выходящего потока.